Rethinking Loss Functions for Fact Verification

We explore loss functions for fact verification in the FEVER shared task. While the cross-entropy loss is a standard objective for training verdict predictors, it fails to capture the heterogeneity among the FEVER verdict classes. In this paper, we develop two task-specific objectives tailored to FEVER. Experimental results confirm that the proposed objective functions outperform the standard cross-entropy. Performance is further improved when these objectives are combined with simple class weighting, which effectively overcomes the imbalance in the training data. The souce code is available at https://github.com/yuta-mukobara/RLF-KGAT

Action Class Relation Detection and Classification Across Multiple Video Datasets

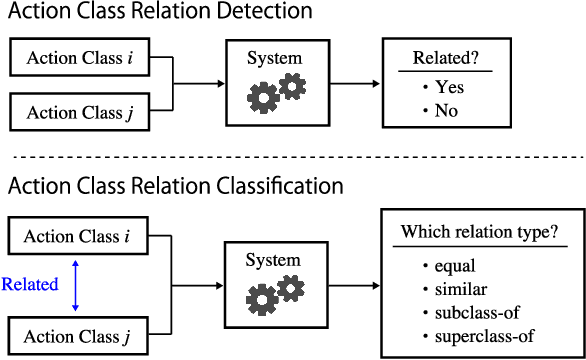
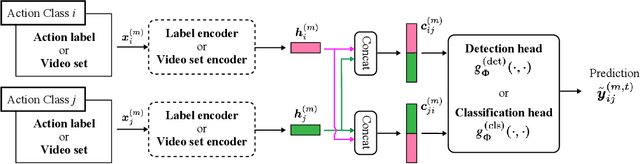
The Meta Video Dataset (MetaVD) provides annotated relations between action classes in major datasets for human action recognition in videos. Although these annotated relations enable dataset augmentation, it is only applicable to those covered by MetaVD. For an external dataset to enjoy the same benefit, the relations between its action classes and those in MetaVD need to be determined. To address this issue, we consider two new machine learning tasks: action class relation detection and classification. We propose a unified model to predict relations between action classes, using language and visual information associated with classes. Experimental results show that (i) pre-trained recent neural network models for texts and videos contribute to high predictive performance, (ii) the relation prediction based on action label texts is more accurate than based on videos, and (iii) a blending approach that combines predictions by both modalities can further improve the predictive performance in some cases.

Learning Decorrelated Representations Efficiently Using Fast Fourier Transform

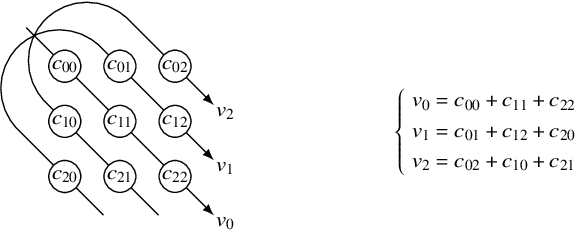
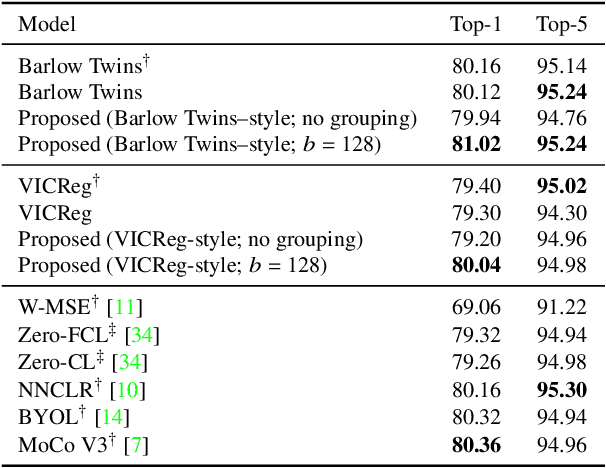
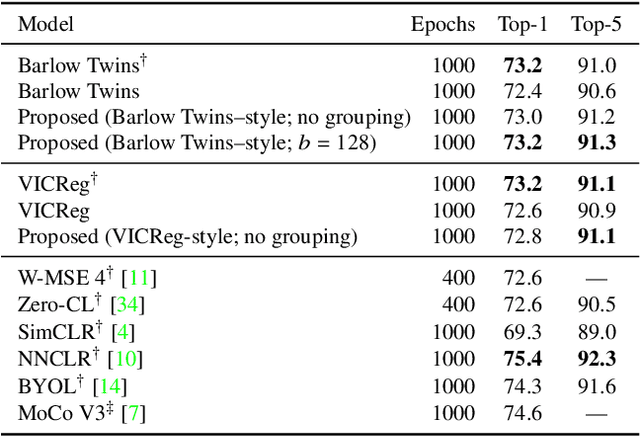
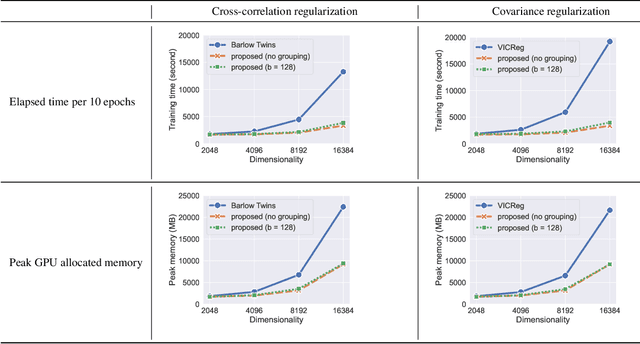
Barlow Twins and VICReg are self-supervised representation learning models that use regularizers to decorrelate features. Although they work as well as conventional representation learning models, their training can be computationally demanding if the dimension of projected representations is high; as these regularizers are defined in terms of individual elements of a cross-correlation or covariance matrix, computing the loss for $d$-dimensional projected representations of $n$ samples takes $O(n d^2)$ time. In this paper, we propose a relaxed version of decorrelating regularizers that can be computed in $O(n d\log d)$ time by the fast Fourier transform. We also propose an inexpensive trick to mitigate the undesirable local minima that develop with the relaxation. Models learning representations using the proposed regularizers show comparable accuracy to existing models in downstream tasks, whereas the training requires less memory and is faster when $d$ is large.

Transductive Data Augmentation with Relational Path Rule Mining for Knowledge Graph Embedding

For knowledge graph completion, two major types of prediction models exist: one based on graph embeddings, and the other based on relation path rule induction. They have different advantages and disadvantages. To take advantage of both types, hybrid models have been proposed recently. One of the hybrid models, UniKER, alternately augments training data by relation path rules and trains an embedding model. Despite its high prediction accuracy, it does not take full advantage of relation path rules, as it disregards low-confidence rules in order to maintain the quality of augmented data. To mitigate this limitation, we propose transductive data augmentation by relation path rules and confidence-based weighting of augmented data. The results and analysis show that our proposed method effectively improves the performance of the embedding model by augmenting data that include true answers or entities similar to them.

Binarized Canonical Polyadic Decomposition for Knowledge Graph Completion

Methods based on vector embeddings of knowledge graphs have been actively pursued as a promising approach to knowledge graph completion.However, embedding models generate storage-inefficient representations, particularly when the number of entities and relations, and the dimensionality of the real-valued embedding vectors are large. We present a binarized CANDECOMP/PARAFAC(CP) decomposition algorithm, which we refer to as B-CP, where real-valued parameters are replaced by binary values to reduce model size. Moreover, we show that a fast score computation technique can be developed with bitwise operations. We prove that B-CP is fully expressive by deriving a bound on the size of its embeddings. Experimental results on several benchmark datasets demonstrate that the proposed method successfully reduces model size by more than an order of magnitude while maintaining task performance at the same level as the real-valued CP model.

A Non-commutative Bilinear Model for Answering Path Queries in Knowledge Graphs

Bilinear diagonal models for knowledge graph embedding (KGE), such as DistMult and ComplEx, balance expressiveness and computational efficiency by representing relations as diagonal matrices. Although they perform well in predicting atomic relations, composite relations (relation paths) cannot be modeled naturally by the product of relation matrices, as the product of diagonal matrices is commutative and hence invariant with the order of relations. In this paper, we propose a new bilinear KGE model, called BlockHolE, based on block circulant matrices. In BlockHolE, relation matrices can be non-commutative, allowing composite relations to be modeled by matrix product. The model is parameterized in a way that covers a spectrum ranging from diagonal to full relation matrices. A fast computation technique is developed on the basis of the duality of the Fourier transform of circulant matrices.

Binarized Knowledge Graph Embeddings

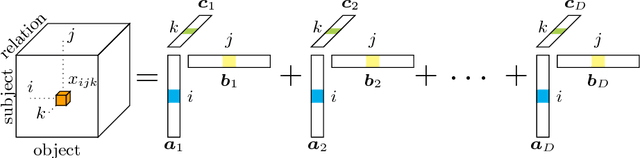
Tensor factorization has become an increasingly popular approach to knowledge graph completion(KGC), which is the task of automatically predicting missing facts in a knowledge graph. However, even with a simple model like CANDECOMP/PARAFAC(CP) tensor decomposition, KGC on existing knowledge graphs is impractical in resource-limited environments, as a large amount of memory is required to store parameters represented as 32-bit or 64-bit floating point numbers. This limitation is expected to become more stringent as existing knowledge graphs, which are already huge, keep steadily growing in scale. To reduce the memory requirement, we present a method for binarizing the parameters of the CP tensor decomposition by introducing a quantization function to the optimization problem. This method replaces floating point-valued parameters with binary ones after training, which drastically reduces the model size at run time. We investigate the trade-off between the quality and size of tensor factorization models for several KGC benchmark datasets. In our experiments, the proposed method successfully reduced the model size by more than an order of magnitude while maintaining the task performance. Moreover, a fast score computation technique can be developed with bitwise operations.

Data-dependent Learning of Symmetric/Antisymmetric Relations for Knowledge Base Completion

Embedding-based methods for knowledge base completion (KBC) learn representations of entities and relations in a vector space, along with the scoring function to estimate the likelihood of relations between entities. The learnable class of scoring functions is designed to be expressive enough to cover a variety of real-world relations, but this expressive comes at the cost of an increased number of parameters. In particular, parameters in these methods are superfluous for relations that are either symmetric or antisymmetric. To mitigate this problem, we propose a new L1 regularizer for Complex Embeddings, which is one of the state-of-the-art embedding-based methods for KBC. This regularizer promotes symmetry or antisymmetry of the scoring function on a relation-by-relation basis, in accordance with the observed data. Our empirical evaluation shows that the proposed method outperforms the original Complex Embeddings and other baseline methods on the FB15k dataset.

A Fast and Easy Regression Technique for k-NN Classification Without Using Negative Pairs

This paper proposes an inexpensive way to learn an effective dissimilarity function to be used for $k$-nearest neighbor ($k$-NN) classification. Unlike Mahalanobis metric learning methods that map both query (unlabeled) objects and labeled objects to new coordinates by a single transformation, our method learns a transformation of labeled objects to new points in the feature space whereas query objects are kept in their original coordinates. This method has several advantages over existing distance metric learning methods: (i) In experiments with large document and image datasets, it achieves $k$-NN classification accuracy better than or at least comparable to the state-of-the-art metric learning methods. (ii) The transformation can be learned efficiently by solving a standard ridge regression problem. For document and image datasets, training is often more than two orders of magnitude faster than the fastest metric learning methods tested. This speed-up is also due to the fact that the proposed method eliminates the optimization over "negative" object pairs, i.e., objects whose class labels are different. (iii) The formulation has a theoretical justification in terms of reducing hubness in data.

On the Equivalence of Holographic and Complex Embeddings for Link Prediction

We show the equivalence of two state-of-the-art link prediction/knowledge graph completion methods: Nickel et al's holographic embedding and Trouillon et al.'s complex embedding. We first consider a spectral version of the holographic embedding, exploiting the frequency domain in the Fourier transform for efficient computation. The analysis of the resulting method reveals that it can be viewed as an instance of the complex embedding with certain constraints cast on the initial vectors upon training. Conversely, any complex embedding can be converted to an equivalent holographic embedding.