Genki Akai
Binarized Canonical Polyadic Decomposition for Knowledge Graph Completion
Dec 04, 2019



Abstract:Methods based on vector embeddings of knowledge graphs have been actively pursued as a promising approach to knowledge graph completion.However, embedding models generate storage-inefficient representations, particularly when the number of entities and relations, and the dimensionality of the real-valued embedding vectors are large. We present a binarized CANDECOMP/PARAFAC(CP) decomposition algorithm, which we refer to as B-CP, where real-valued parameters are replaced by binary values to reduce model size. Moreover, we show that a fast score computation technique can be developed with bitwise operations. We prove that B-CP is fully expressive by deriving a bound on the size of its embeddings. Experimental results on several benchmark datasets demonstrate that the proposed method successfully reduces model size by more than an order of magnitude while maintaining task performance at the same level as the real-valued CP model.
Binarized Knowledge Graph Embeddings
Feb 08, 2019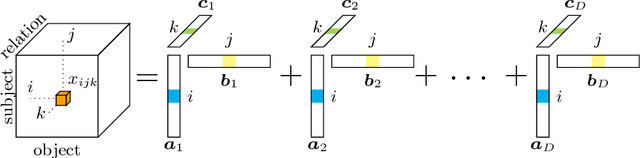



Abstract:Tensor factorization has become an increasingly popular approach to knowledge graph completion(KGC), which is the task of automatically predicting missing facts in a knowledge graph. However, even with a simple model like CANDECOMP/PARAFAC(CP) tensor decomposition, KGC on existing knowledge graphs is impractical in resource-limited environments, as a large amount of memory is required to store parameters represented as 32-bit or 64-bit floating point numbers. This limitation is expected to become more stringent as existing knowledge graphs, which are already huge, keep steadily growing in scale. To reduce the memory requirement, we present a method for binarizing the parameters of the CP tensor decomposition by introducing a quantization function to the optimization problem. This method replaces floating point-valued parameters with binary ones after training, which drastically reduces the model size at run time. We investigate the trade-off between the quality and size of tensor factorization models for several KGC benchmark datasets. In our experiments, the proposed method successfully reduced the model size by more than an order of magnitude while maintaining the task performance. Moreover, a fast score computation technique can be developed with bitwise operations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge