Improving Consistency Models with Generator-Induced Coupling

Consistency models are promising generative models as they distill the multi-step sampling of score-based diffusion in a single forward pass of a neural network. Without access to sampling trajectories of a pre-trained diffusion model, consistency training relies on proxy trajectories built on an independent coupling between the noise and data distributions. Refining this coupling is a key area of improvement to make it more adapted to the task and reduce the resulting randomness in the training process. In this work, we introduce a novel coupling associating the input noisy data with their generated output from the consistency model itself, as a proxy to the inaccessible diffusion flow output. Our affordable approach exploits the inherent capacity of consistency models to compute the transport map in a single step. We provide intuition and empirical evidence of the relevance of our generator-induced coupling (GC), which brings consistency training closer to score distillation. Consequently, our method not only accelerates consistency training convergence by significant amounts but also enhances the resulting performance. The code is available at: https://github.com/thibautissenhuth/consistency_GC.

Gaussian-Smoothed Sliced Probability Divergences

Gaussian smoothed sliced Wasserstein distance has been recently introduced for comparing probability distributions, while preserving privacy on the data. It has been shown that it provides performances similar to its non-smoothed (non-private) counterpart. However, the computationaland statistical properties of such a metric have not yet been well-established. This work investigates the theoretical properties of this distance as well as those of generalized versions denoted as Gaussian-smoothed sliced divergences. We first show that smoothing and slicing preserve the metric property and the weak topology. To study the sample complexity of such divergences, we then introduce $\hat{\hat\mu}_{n}$ the double empirical distribution for the smoothed-projected $\mu$. The distribution $\hat{\hat\mu}_{n}$ is a result of a double sampling process: one from sampling according to the origin distribution $\mu$ and the second according to the convolution of the projection of $\mu$ on the unit sphere and the Gaussian smoothing. We particularly focus on the Gaussian smoothed sliced Wasserstein distance and prove that it converges with a rate $O(n^{-1/2})$. We also derive other properties, including continuity, of different divergences with respect to the smoothing parameter. We support our theoretical findings with empirical studies in the context of privacy-preserving domain adaptation.

Differentially Private Gradient Flow based on the Sliced Wasserstein Distance for Non-Parametric Generative Modeling

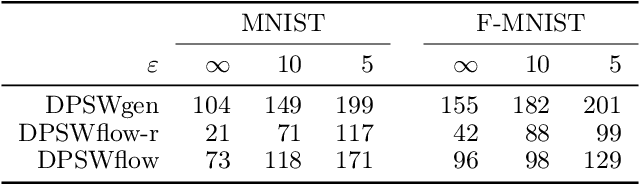
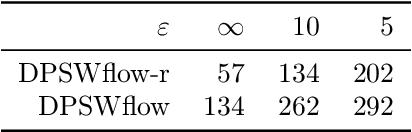
Safeguarding privacy in sensitive training data is paramount, particularly in the context of generative modeling. This is done through either differentially private stochastic gradient descent, or with a differentially private metric for training models or generators. In this paper, we introduce a novel differentially private generative modeling approach based on parameter-free gradient flows in the space of probability measures. The proposed algorithm is a new discretized flow which operates through a particle scheme, utilizing drift derived from the sliced Wasserstein distance and computed in a private manner. Our experiments show that compared to a generator-based model, our proposed model can generate higher-fidelity data at a low privacy budget, offering a viable alternative to generator-based approaches.

Federated Wasserstein Distance

We introduce a principled way of computing the Wasserstein distance between two distributions in a federated manner. Namely, we show how to estimate the Wasserstein distance between two samples stored and kept on different devices/clients whilst a central entity/server orchestrates the computations (again, without having access to the samples). To achieve this feat, we take advantage of the geometric properties of the Wasserstein distance -- in particular, the triangle inequality -- and that of the associated {\em geodesics}: our algorithm, FedWad (for Federated Wasserstein Distance), iteratively approximates the Wasserstein distance by manipulating and exchanging distributions from the space of geodesics in lieu of the input samples. In addition to establishing the convergence properties of FedWad, we provide empirical results on federated coresets and federate optimal transport dataset distance, that we respectively exploit for building a novel federated model and for boosting performance of popular federated learning algorithms.

Adversarial Sample Detection Through Neural Network Transport Dynamics

We propose a detector of adversarial samples that is based on the view of neural networks as discrete dynamic systems. The detector tells clean inputs from abnormal ones by comparing the discrete vector fields they follow through the layers. We also show that regularizing this vector field during training makes the network more regular on the data distribution's support, thus making the activations of clean inputs more distinguishable from those of abnormal ones. Experimentally, we compare our detector favorably to other detectors on seen and unseen attacks, and show that the regularization of the network's dynamics improves the performance of adversarial detectors that use the internal embeddings as inputs, while also improving test accuracy.

Unifying GANs and Score-Based Diffusion as Generative Particle Models

Particle-based deep generative models, such as gradient flows and score-based diffusion models, have recently gained traction thanks to their striking performance. Their principle of displacing particle distributions by differential equations is conventionally seen as opposed to the previously widespread generative adversarial networks (GANs), which involve training a pushforward generator network. In this paper, we challenge this interpretation and propose a novel framework that unifies particle and adversarial generative models by framing generator training as a generalization of particle models. This suggests that a generator is an optional addition to any such generative model. Consequently, integrating a generator into a score-based diffusion model and training a GAN without a generator naturally emerge from our framework. We empirically test the viability of these original models as proofs of concepts of potential applications of our framework.

Sliced-Wasserstein on Symmetric Positive Definite Matrices for M/EEG Signals

When dealing with electro or magnetoencephalography records, many supervised prediction tasks are solved by working with covariance matrices to summarize the signals. Learning with these matrices requires using Riemanian geometry to account for their structure. In this paper, we propose a new method to deal with distributions of covariance matrices and demonstrate its computational efficiency on M/EEG multivariate time series. More specifically, we define a Sliced-Wasserstein distance between measures of symmetric positive definite matrices that comes with strong theoretical guarantees. Then, we take advantage of its properties and kernel methods to apply this distance to brain-age prediction from MEG data and compare it to state-of-the-art algorithms based on Riemannian geometry. Finally, we show that it is an efficient surrogate to the Wasserstein distance in domain adaptation for Brain Computer Interface applications.

Approximating DTW with a convolutional neural network on EEG data

Dynamic Time Wrapping (DTW) is a widely used algorithm for measuring similarities between two time series. It is especially valuable in a wide variety of applications, such as clustering, anomaly detection, classification, or video segmentation, where the time-series have different timescales, are irregularly sampled, or are shifted. However, it is not prone to be considered as a loss function in an end-to-end learning framework because of its non-differentiability and its quadratic temporal complexity. While differentiable variants of DTW have been introduced by the community, they still present some drawbacks: computing the distance is still expensive and this similarity tends to blur some differences in the time-series. In this paper, we propose a fast and differentiable approximation of DTW by comparing two architectures: the first one for learning an embedding in which the Euclidean distance mimics the DTW, and the second one for directly predicting the DTW output using regression. We build the former by training a siamese neural network to regress the DTW value between two time-series. Depending on the nature of the activation function, this approximation naturally supports differentiation, and it is efficient to compute. We show, in a time-series retrieval context on EEG datasets, that our methods achieve at least the same level of accuracy as other DTW main approximations with higher computational efficiency. We also show that it can be used to learn in an end-to-end setting on long time series by proposing generative models of EEGs.

Personalised Federated Learning On Heterogeneous Feature Spaces

Most personalised federated learning (FL) approaches assume that raw data of all clients are defined in a common subspace i.e. all clients store their data according to the same schema. For real-world applications, this assumption is restrictive as clients, having their own systems to collect and then store data, may use heterogeneous data representations. We aim at filling this gap. To this end, we propose a general framework coined FLIC that maps client's data onto a common feature space via local embedding functions. The common feature space is learnt in a federated manner using Wasserstein barycenters while the local embedding functions are trained on each client via distribution alignment. We integrate this distribution alignement mechanism into a federated learning approach and provide the algorithmics of FLIC. We compare its performances against FL benchmarks involving heterogeneous input features spaces. In addition, we provide theoretical insights supporting the relevance of our methodology.

Continuous PDE Dynamics Forecasting with Implicit Neural Representations

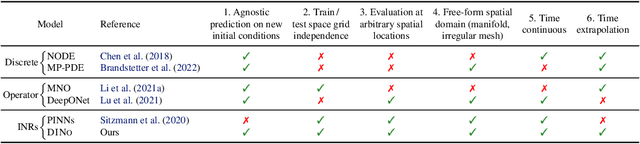
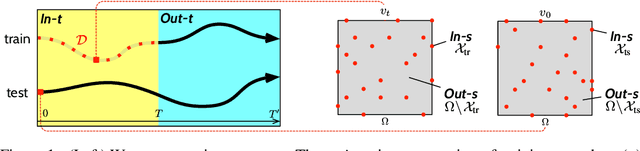
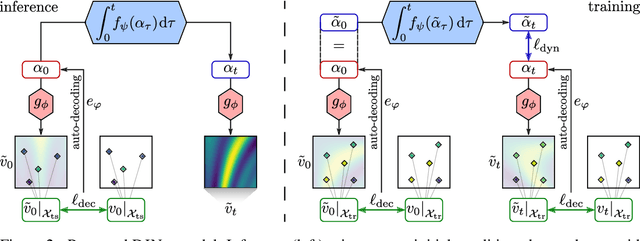
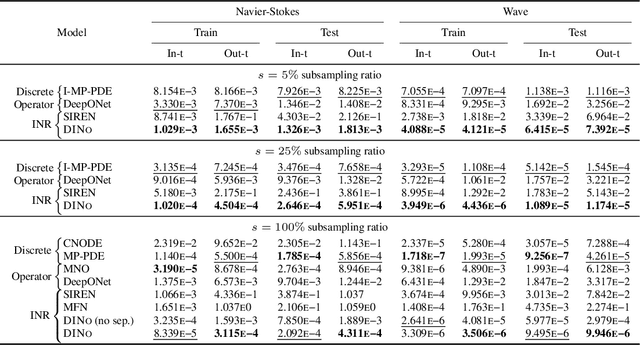
Effective data-driven PDE forecasting methods often rely on fixed spatial and / or temporal discretizations. This raises limitations in real-world applications like weather prediction where flexible extrapolation at arbitrary spatiotemporal locations is required. We address this problem by introducing a new data-driven approach, DINo, that models a PDE's flow with continuous-time dynamics of spatially continuous functions. This is achieved by embedding spatial observations independently of their discretization via Implicit Neural Representations in a small latent space temporally driven by a learned ODE. This separate and flexible treatment of time and space makes DINo the first data-driven model to combine the following advantages. It extrapolates at arbitrary spatial and temporal locations; it can learn from sparse irregular grids or manifolds; at test time, it generalizes to new grids or resolutions. DINo outperforms alternative neural PDE forecasters in a variety of challenging generalization scenarios on representative PDE systems.