Distribution-Aware Mean Estimation under User-level Local Differential Privacy

We consider the problem of mean estimation under user-level local differential privacy, where $n$ users are contributing through their local pool of data samples. Previous work assume that the number of data samples is the same across users. In contrast, we consider a more general and realistic scenario where each user $u \in [n]$ owns $m_u$ data samples drawn from some generative distribution $\mu$; $m_u$ being unknown to the statistician but drawn from a known distribution $M$ over $\mathbb{N}^\star$. Based on a distribution-aware mean estimation algorithm, we establish an $M$-dependent upper bounds on the worst-case risk over $\mu$ for the task of mean estimation. We then derive a lower bound. The two bounds are asymptotically matching up to logarithmic factors and reduce to known bounds when $m_u = m$ for any user $u$.

DU-Shapley: A Shapley Value Proxy for Efficient Dataset Valuation

Many machine learning problems require performing dataset valuation, i.e. to quantify the incremental gain, to some relevant pre-defined utility, of aggregating an individual dataset to others. As seminal examples, dataset valuation has been leveraged in collaborative and federated learning to create incentives for data sharing across several data owners. The Shapley value has recently been proposed as a principled tool to achieve this goal due to formal axiomatic justification. Since its computation often requires exponential time, standard approximation strategies based on Monte Carlo integration have been considered. Such generic approximation methods, however, remain expensive in some cases. In this paper, we exploit the knowledge about the structure of the dataset valuation problem to devise more efficient Shapley value estimators. We propose a novel approximation of the Shapley value, referred to as discrete uniform Shapley (DU-Shapley) which is expressed as an expectation under a discrete uniform distribution with support of reasonable size. We justify the relevancy of the proposed framework via asymptotic and non-asymptotic theoretical guarantees and show that DU-Shapley tends towards the Shapley value when the number of data owners is large. The benefits of the proposed framework are finally illustrated on several dataset valuation benchmarks. DU-Shapley outperforms other Shapley value approximations, even when the number of data owners is small.

Personalised Federated Learning On Heterogeneous Feature Spaces

Most personalised federated learning (FL) approaches assume that raw data of all clients are defined in a common subspace i.e. all clients store their data according to the same schema. For real-world applications, this assumption is restrictive as clients, having their own systems to collect and then store data, may use heterogeneous data representations. We aim at filling this gap. To this end, we propose a general framework coined FLIC that maps client's data onto a common feature space via local embedding functions. The common feature space is learnt in a federated manner using Wasserstein barycenters while the local embedding functions are trained on each client via distribution alignment. We integrate this distribution alignement mechanism into a federated learning approach and provide the algorithmics of FLIC. We compare its performances against FL benchmarks involving heterogeneous input features spaces. In addition, we provide theoretical insights supporting the relevance of our methodology.

FedPop: A Bayesian Approach for Personalised Federated Learning

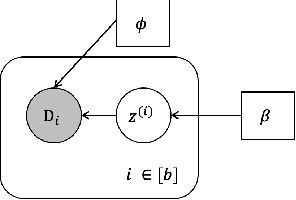
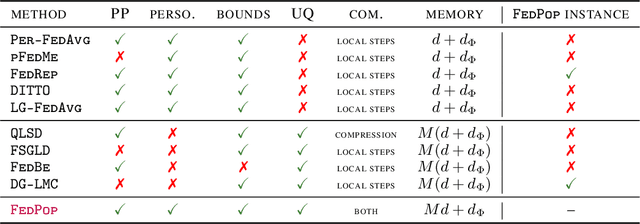
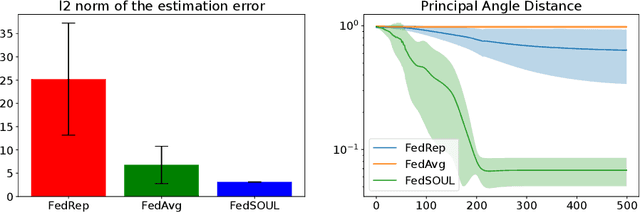
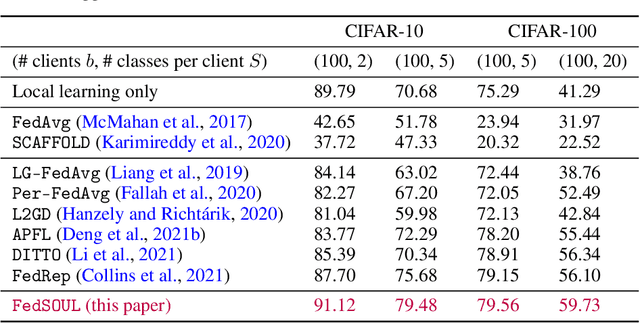
Personalised federated learning (FL) aims at collaboratively learning a machine learning model taylored for each client. Albeit promising advances have been made in this direction, most of existing approaches works do not allow for uncertainty quantification which is crucial in many applications. In addition, personalisation in the cross-device setting still involves important issues, especially for new clients or those having small number of observations. This paper aims at filling these gaps. To this end, we propose a novel methodology coined FedPop by recasting personalised FL into the population modeling paradigm where clients' models involve fixed common population parameters and random effects, aiming at explaining data heterogeneity. To derive convergence guarantees for our scheme, we introduce a new class of federated stochastic optimisation algorithms which relies on Markov chain Monte Carlo methods. Compared to existing personalised FL methods, the proposed methodology has important benefits: it is robust to client drift, practical for inference on new clients, and above all, enables uncertainty quantification under mild computational and memory overheads. We provide non-asymptotic convergence guarantees for the proposed algorithms and illustrate their performances on various personalised federated learning tasks.

DG-LMC: A Turn-key and Scalable Synchronous Distributed MCMC Algorithm via Langevin Monte Carlo within Gibbs

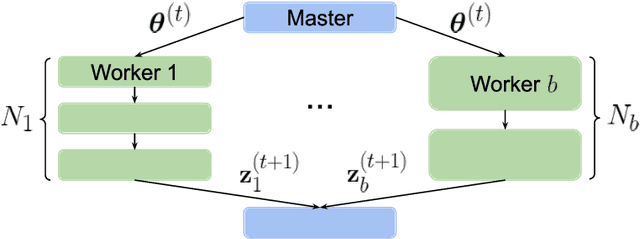
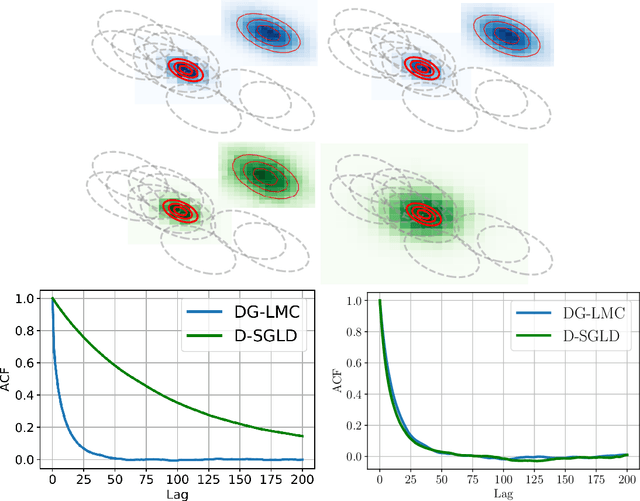
Performing reliable Bayesian inference on a big data scale is becoming a keystone in the modern era of machine learning. A workhorse class of methods to achieve this task are Markov chain Monte Carlo (MCMC) algorithms and their design to handle distributed datasets has been the subject of many works. However, existing methods are not completely either reliable or computationally efficient. In this paper, we propose to fill this gap in the case where the dataset is partitioned and stored on computing nodes within a cluster under a master/slaves architecture. We derive a user-friendly centralised distributed MCMC algorithm with provable scaling in high-dimensional settings. We illustrate the relevance of the proposed methodology on both synthetic and real data experiments.

QLSD: Quantised Langevin stochastic dynamics for Bayesian federated learning

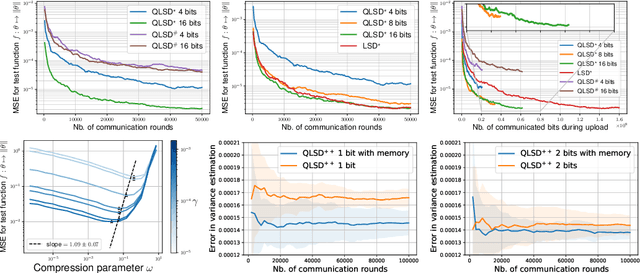
Federated learning aims at conducting inference when data are decentralised and locally stored on several clients, under two main constraints: data ownership and communication overhead. In this paper, we address these issues under the Bayesian paradigm. To this end, we propose a novel Markov chain Monte Carlo algorithm coined \texttt{QLSD} built upon quantised versions of stochastic gradient Langevin dynamics. To improve performance in a big data regime, we introduce variance-reduced alternatives of our methodology referred to as \texttt{QLSD}$^\star$ and \texttt{QLSD}$^{++}$. We provide both non-asymptotic and asymptotic convergence guarantees for the proposed algorithms and illustrate their benefits on several federated learning benchmarks.

Efficient MCMC Sampling with Dimension-Free Convergence Rate using ADMM-type Splitting

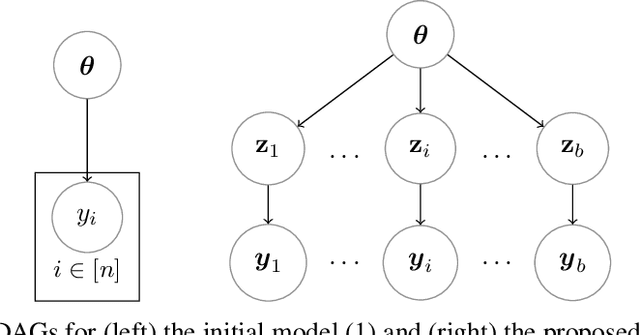
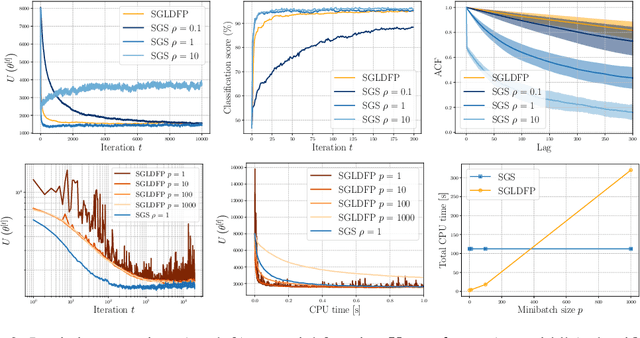
Performing exact Bayesian inference for complex models is intractable. Markov chain Monte Carlo (MCMC) algorithms can provide reliable approximations of the posterior distribution but are computationally expensive for large datasets. A standard approach to mitigate this complexity consists of using subsampling techniques or distributing the data across a cluster. However, these approaches are typically unreliable in high-dimensional scenarios. We focus here on an alternative class of MCMC schemes exploiting a splitting strategy akin to the one used by the celebrated ADMM optimization algorithm. These methods, proposed recently in [43, 51], appear to provide empirically state-of-the-art performance. We generalize here these ideas and propose a detailed theoretical study of one of these algorithms known as the Split Gibbs Sampler. Under regularity conditions, we establish explicit dimension-free convergence rates for this scheme using Ricci curvature and coupling ideas. We demonstrate experimentally the excellent performance of these MCMC schemes on various applications.

Asymptotically exact data augmentation: models, properties and algorithms

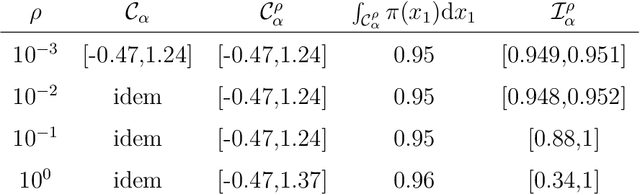
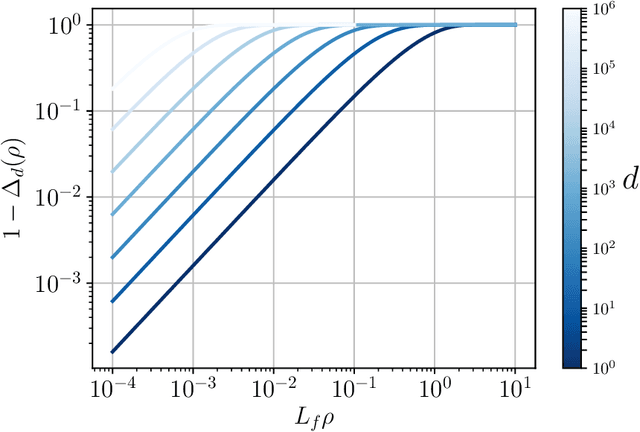
Data augmentation, by the introduction of auxiliary variables, has become an ubiquitous technique to improve mixing/convergence properties, simplify the implementation or reduce the computational time of inference methods such as Markov chain Monte Carlo. Nonetheless, introducing appropriate auxiliary variables while preserving the initial target probability distribution cannot be conducted in a systematic way but highly depends on the considered problem. To deal with such issues, this paper draws a unified framework, namely asymptotically exact data augmentation (AXDA), which encompasses several well-established but also more recent approximate augmented models. Benefiting from a much more general perspective, it delivers some additional qualitative and quantitative insights concerning these schemes. In particular, general properties of AXDA along with non-asymptotic theoretical results on the approximation that is made are stated. Close connections to existing Bayesian methods (e.g. mixture modeling, robust Bayesian models and approximate Bayesian computation) are also drawn. All the results are illustrated with examples and applied to standard statistical learning problems.