On the Impact of the Utility in Semivalue-based Data Valuation

Semivalue-based data valuation in machine learning (ML) quantifies the contribution of individual data points to a downstream ML task by leveraging principles from cooperative game theory and the notion of utility. While this framework has been used in practice for assessing data quality, our experiments reveal inconsistent valuation outcomes across different utilities, albeit all related to ML performance. Beyond raising concerns about the reliability of data valuation, this inconsistency is challenging to interpret, as it stems from the complex interaction of the utility with data points and semivalue weights, which has barely been studied in prior work. In this paper, we take a first step toward clarifying the utility impact on semivalue-based data valuation. Specifically, we provide geometric interpretations of this impact for a broad family of classification utilities, which includes the accuracy and the arithmetic mean. We introduce the notion of spatial signatures: given a semivalue, data points can be embedded into a two-dimensional space, and utility functions map to the dual of this space. This geometric perspective separates the influence of the dataset and semivalue from that of the utility, providing a theoretical explanation for the experimentally observed sensitivity of valuation outcomes to the utility choice.

Trading-off price for data quality to achieve fair online allocation

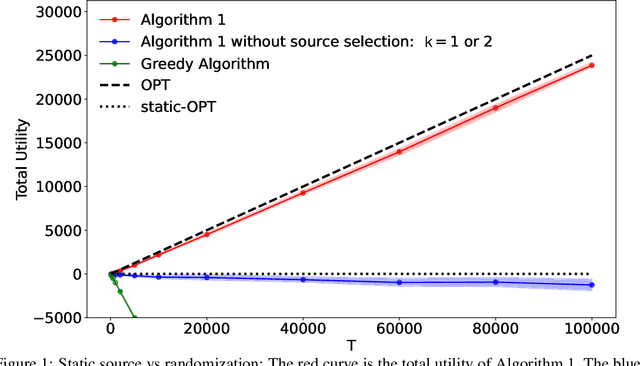
We consider the problem of online allocation subject to a long-term fairness penalty. Contrary to existing works, however, we do not assume that the decision-maker observes the protected attributes -- which is often unrealistic in practice. Instead they can purchase data that help estimate them from sources of different quality; and hence reduce the fairness penalty at some cost. We model this problem as a multi-armed bandit problem where each arm corresponds to the choice of a data source, coupled with the online allocation problem. We propose an algorithm that jointly solves both problems and show that it has a regret bounded by $\mathcal{O}(\sqrt{T})$. A key difficulty is that the rewards received by selecting a source are correlated by the fairness penalty, which leads to a need for randomization (despite a stochastic setting). Our algorithm takes into account contextual information available before the source selection, and can adapt to many different fairness notions. We also show that in some instances, the estimates used can be learned on the fly.

DU-Shapley: A Shapley Value Proxy for Efficient Dataset Valuation

Many machine learning problems require performing dataset valuation, i.e. to quantify the incremental gain, to some relevant pre-defined utility, of aggregating an individual dataset to others. As seminal examples, dataset valuation has been leveraged in collaborative and federated learning to create incentives for data sharing across several data owners. The Shapley value has recently been proposed as a principled tool to achieve this goal due to formal axiomatic justification. Since its computation often requires exponential time, standard approximation strategies based on Monte Carlo integration have been considered. Such generic approximation methods, however, remain expensive in some cases. In this paper, we exploit the knowledge about the structure of the dataset valuation problem to devise more efficient Shapley value estimators. We propose a novel approximation of the Shapley value, referred to as discrete uniform Shapley (DU-Shapley) which is expressed as an expectation under a discrete uniform distribution with support of reasonable size. We justify the relevancy of the proposed framework via asymptotic and non-asymptotic theoretical guarantees and show that DU-Shapley tends towards the Shapley value when the number of data owners is large. The benefits of the proposed framework are finally illustrated on several dataset valuation benchmarks. DU-Shapley outperforms other Shapley value approximations, even when the number of data owners is small.

Bounding and Approximating Intersectional Fairness through Marginal Fairness

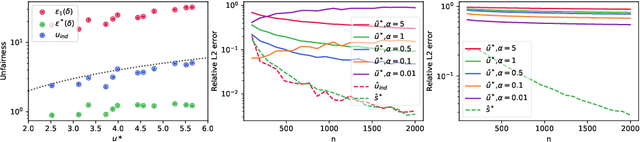
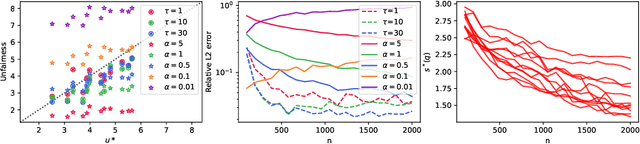
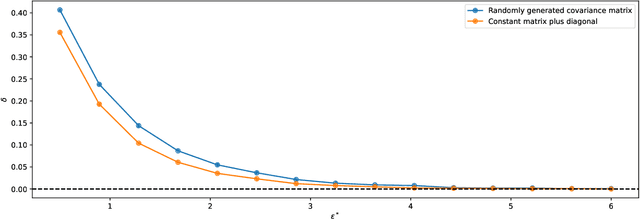
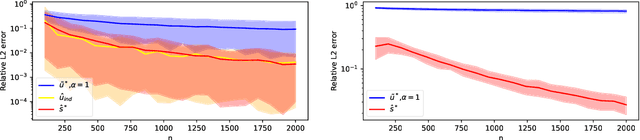
Discrimination in machine learning often arises along multiple dimensions (a.k.a. protected attributes); it is then desirable to ensure \emph{intersectional fairness} -- i.e., that no subgroup is discriminated against. It is known that ensuring \emph{marginal fairness} for every dimension independently is not sufficient in general. Due to the exponential number of subgroups, however, directly measuring intersectional fairness from data is impossible. In this paper, our primary goal is to understand in detail the relationship between marginal and intersectional fairness through statistical analysis. We first identify a set of sufficient conditions under which an exact relationship can be obtained. Then, we prove bounds (easily computable through marginal fairness and other meaningful statistical quantities) in high-probability on intersectional fairness in the general case. Beyond their descriptive value, we show that these theoretical bounds can be leveraged to derive a heuristic improving the approximation and bounds of intersectional fairness by choosing, in a relevant manner, protected attributes for which we describe intersectional subgroups. Finally, we test the performance of our approximations and bounds on real and synthetic data-sets.

Pareto-Optimal Fairness-Utility Amortizations in Rankings with a DBN Exposure Model

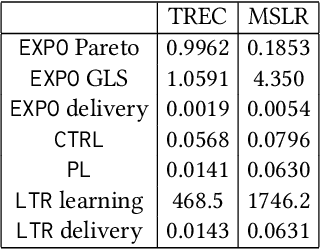
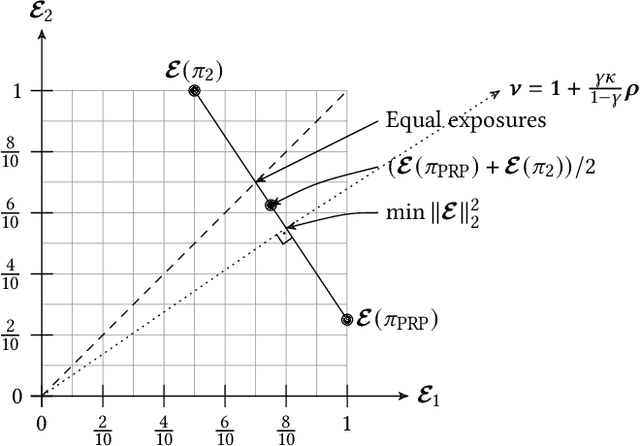
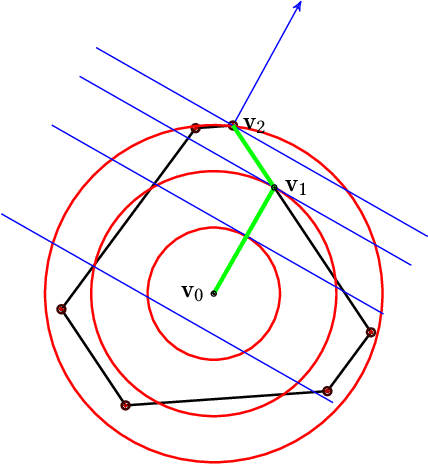
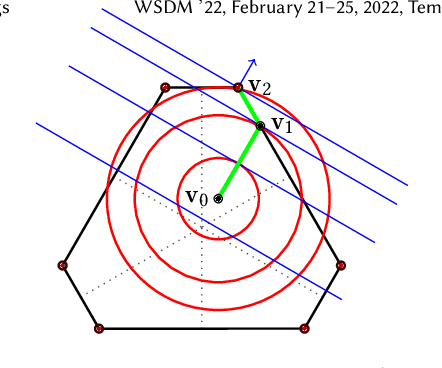
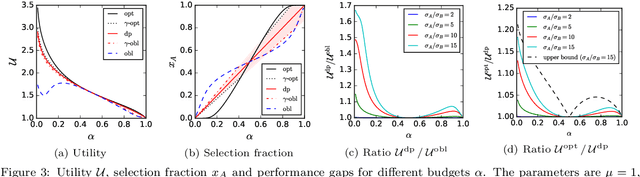
In recent years, it has become clear that rankings delivered in many areas need not only be useful to the users but also respect fairness of exposure for the item producers. We consider the problem of finding ranking policies that achieve a Pareto-optimal tradeoff between these two aspects. Several methods were proposed to solve it; for instance a popular one is to use linear programming with a Birkhoff-von Neumann decomposition. These methods, however, are based on a classical Position Based exposure Model (PBM), which assumes independence between the items (hence the exposure only depends on the rank). In many applications, this assumption is unrealistic and the community increasingly moves towards considering other models that include dependences, such as the Dynamic Bayesian Network (DBN) exposure model. For such models, computing (exact) optimal fair ranking policies remains an open question. We answer this question by leveraging a new geometrical method based on the so-called expohedron proposed recently for the PBM (Kletti et al., WSDM'22). We lay out the structure of a new geometrical object (the DBN-expohedron), and propose for it a Carath\'eodory decomposition algorithm of complexity $O(n^3)$, where $n$ is the number of documents to rank. Such an algorithm enables expressing any feasible expected exposure vector as a distribution over at most $n$ rankings; furthermore we show that we can compute the whole set of Pareto-optimal expected exposure vectors with the same complexity $O(n^3)$. Our work constitutes the first exact algorithm able to efficiently find a Pareto-optimal distribution of rankings. It is applicable to a broad range of fairness notions, including classical notions of meritocratic and demographic fairness. We empirically evaluate our method on the TREC2020 and MSLR datasets and compare it to several baselines in terms of Pareto-optimality and speed.

Introducing the Expohedron for Efficient Pareto-optimal Fairness-Utility Amortizations in Repeated Rankings

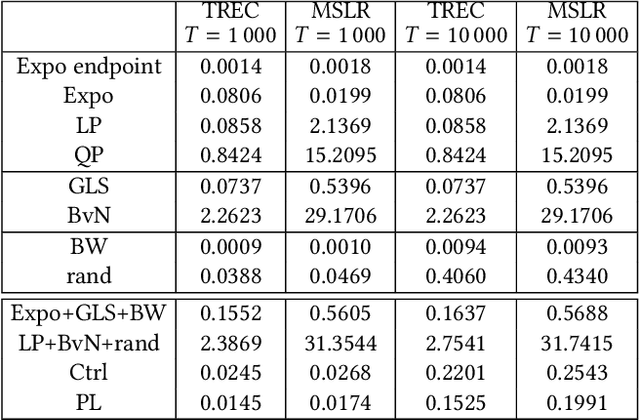
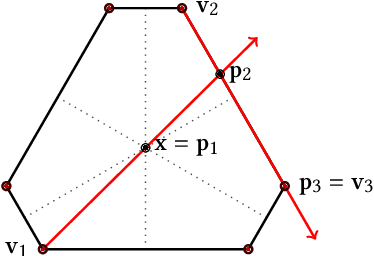
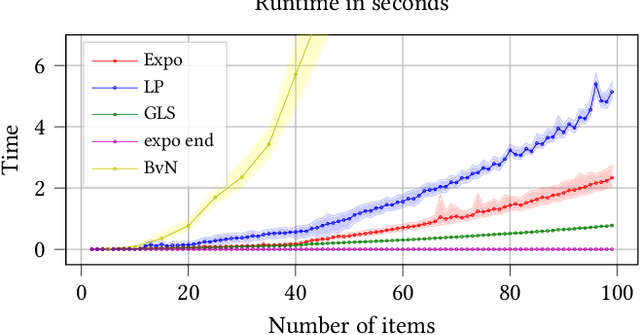
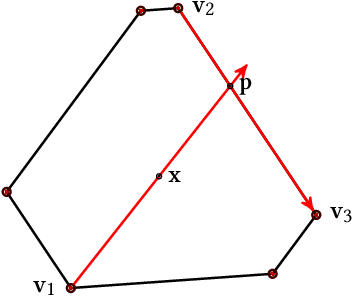
We consider the problem of computing a sequence of rankings that maximizes consumer-side utility while minimizing producer-side individual unfairness of exposure. While prior work has addressed this problem using linear or quadratic programs on bistochastic matrices, such approaches, relying on Birkhoff-von Neumann (BvN) decompositions, are too slow to be implemented at large scale. In this paper we introduce a geometrical object, a polytope that we call expohedron, whose points represent all achievable exposures of items for a Position Based Model (PBM). We exhibit some of its properties and lay out a Carath\'eodory decomposition algorithm with complexity $O(n^2\log(n))$ able to express any point inside the expohedron as a convex sum of at most $n$ vertices, where $n$ is the number of items to rank. Such a decomposition makes it possible to express any feasible target exposure as a distribution over at most $n$ rankings. Furthermore we show that we can use this polytope to recover the whole Pareto frontier of the multi-objective fairness-utility optimization problem, using a simple geometrical procedure with complexity $O(n^2\log(n))$. Our approach compares favorably to linear or quadratic programming baselines in terms of algorithmic complexity and empirical runtime and is applicable to any merit that is a non-decreasing function of item relevance. Furthermore our solution can be expressed as a distribution over only $n$ permutations, instead of the $(n-1)^2 + 1$ achieved with BvN decompositions. We perform experiments on synthetic and real-world datasets, confirming our theoretical results.

On Fair Selection in the Presence of Implicit and Differential Variance

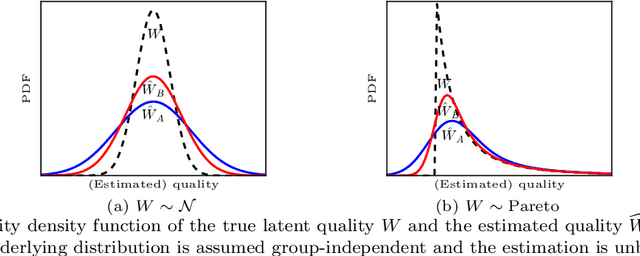
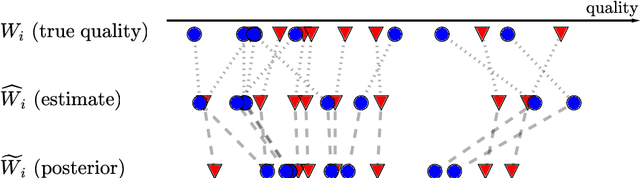
Discrimination in selection problems such as hiring or college admission is often explained by implicit bias from the decision maker against disadvantaged demographic groups. In this paper, we consider a model where the decision maker receives a noisy estimate of each candidate's quality, whose variance depends on the candidate's group -- we argue that such differential variance is a key feature of many selection problems. We analyze two notable settings: in the first, the noise variances are unknown to the decision maker who simply picks the candidates with the highest estimated quality independently of their group; in the second, the variances are known and the decision maker picks candidates having the highest expected quality given the noisy estimate. We show that both baseline decision makers yield discrimination, although in opposite directions: the first leads to underrepresentation of the low-variance group while the second leads to underrepresentation of the high-variance group. We study the effect on the selection utility of imposing a fairness mechanism that we term the $\gamma$-rule (it is an extension of the classical four-fifths rule and it also includes demographic parity). In the first setting (with unknown variances), we prove that under mild conditions, imposing the $\gamma$-rule increases the selection utility -- here there is no trade-off between fairness and utility. In the second setting (with known variances), imposing the $\gamma$-rule decreases the utility but we prove a bound on the utility loss due to the fairness mechanism.

Scalable Optimal Classifiers for Adversarial Settings under Uncertainty

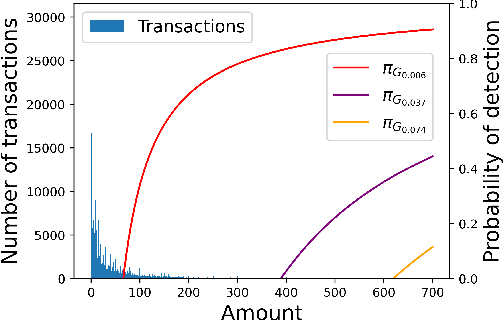
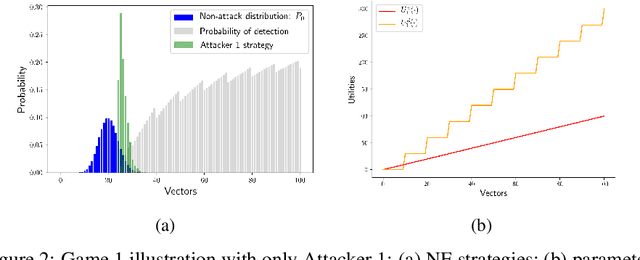
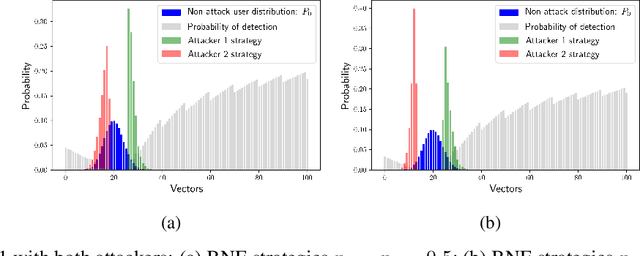
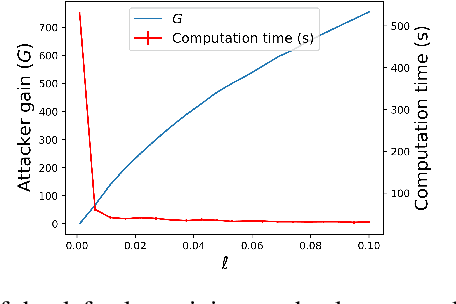
We consider the problem of finding optimal classifiers in an adversarial setting where the class-1 data is generated by an attacker whose objective is not known to the defender -- an aspect that is key to realistic applications but has so far been overlooked in the literature. To model this situation, we propose a Bayesian game framework where the defender chooses a classifier with no a priori restriction on the set of possible classifiers. The key difficulty in the proposed framework is that the set of possible classifiers is exponential in the set of possible data, which is itself exponential in the number of features used for classification. To counter this, we first show that Bayesian Nash equilibria can be characterized completely via functional threshold classifiers with a small number of parameters. We then show that this low-dimensional characterization enables to develop a training method to compute provably approximately optimal classifiers in a scalable manner; and to develop a learning algorithm for the online setting with low regret (both independent of the dimension of the set of possible data). We illustrate our results through simulations.

On Fair Selection in the Presence of Implicit Variance

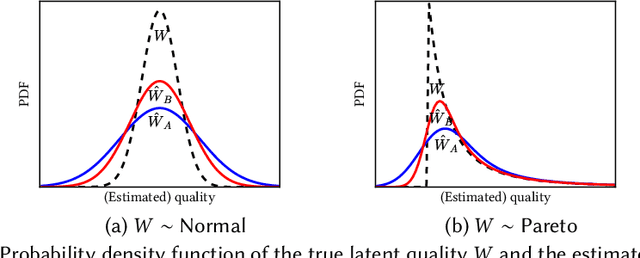
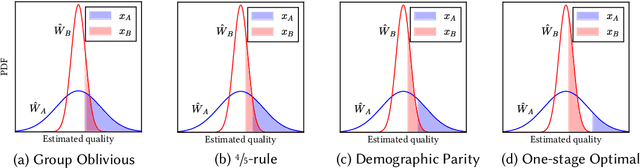
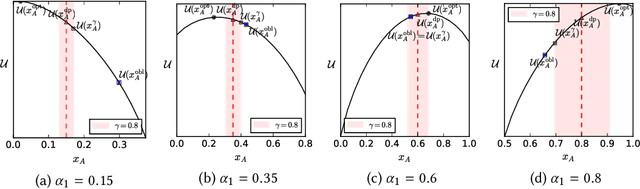
Quota-based fairness mechanisms like the so-called Rooney rule or four-fifths rule are used in selection problems such as hiring or college admission to reduce inequalities based on sensitive demographic attributes. These mechanisms are often viewed as introducing a trade-off between selection fairness and utility. In recent work, however, Kleinberg and Raghavan showed that, in the presence of implicit bias in estimating candidates' quality, the Rooney rule can increase the utility of the selection process. We argue that even in the absence of implicit bias, the estimates of candidates' quality from different groups may differ in another fundamental way, namely, in their variance. We term this phenomenon implicit variance and we ask: can fairness mechanisms be beneficial to the utility of a selection process in the presence of implicit variance (even in the absence of implicit bias)? To answer this question, we propose a simple model in which candidates have a true latent quality that is drawn from a group-independent normal distribution. To make the selection, a decision maker receives an unbiased estimate of the quality of each candidate, with normal noise, but whose variance depends on the candidate's group. We then compare the utility obtained by imposing a fairness mechanism that we term $\gamma$-rule (it includes demographic parity and the four-fifths rule as special cases), to that of a group-oblivious selection algorithm that picks the candidates with the highest estimated quality independently of their group. Our main result shows that the demographic parity mechanism always increases the selection utility, while any $\gamma$-rule weakly increases it. We extend our model to a two-stage selection process where the true quality is observed at the second stage. We discuss multiple extensions of our results, in particular to different distributions of the true latent quality.

Nonzero-sum Adversarial Hypothesis Testing Games

We study nonzero-sum hypothesis testing games that arise in the context of adversarial classification, in both the Bayesian as well as the Neyman-Pearson frameworks. We first show that these games admit mixed strategy Nash equilibria, and then we examine some interesting concentration phenomena of these equilibria. Our main results are on the exponential rates of convergence of classification errors at equilibrium, which are analogous to the well-known Chernoff-Stein lemma and Chernoff information that describe the error exponents in the classical binary hypothesis testing problem, but with parameters derived from the adversarial model. The results are validated through numerical experiments.