Trading-off price for data quality to achieve fair online allocation

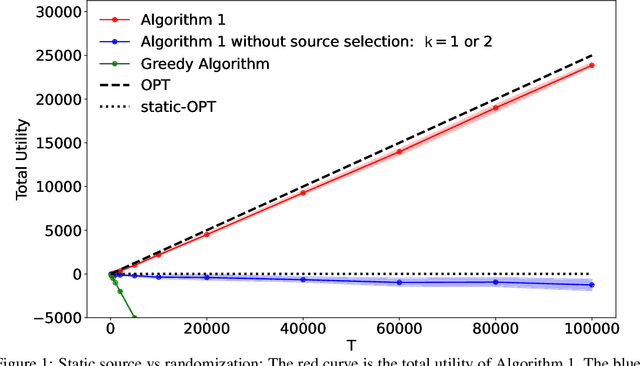
We consider the problem of online allocation subject to a long-term fairness penalty. Contrary to existing works, however, we do not assume that the decision-maker observes the protected attributes -- which is often unrealistic in practice. Instead they can purchase data that help estimate them from sources of different quality; and hence reduce the fairness penalty at some cost. We model this problem as a multi-armed bandit problem where each arm corresponds to the choice of a data source, coupled with the online allocation problem. We propose an algorithm that jointly solves both problems and show that it has a regret bounded by $\mathcal{O}(\sqrt{T})$. A key difficulty is that the rewards received by selecting a source are correlated by the fairness penalty, which leads to a need for randomization (despite a stochastic setting). Our algorithm takes into account contextual information available before the source selection, and can adapt to many different fairness notions. We also show that in some instances, the estimates used can be learned on the fly.

Bounding and Approximating Intersectional Fairness through Marginal Fairness

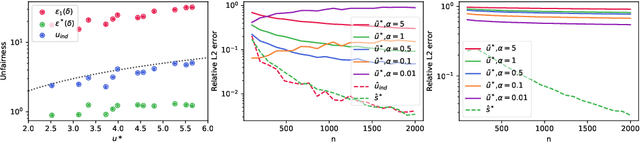
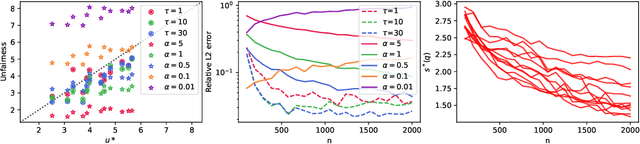
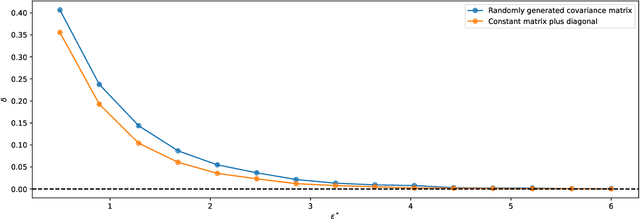
Discrimination in machine learning often arises along multiple dimensions (a.k.a. protected attributes); it is then desirable to ensure \emph{intersectional fairness} -- i.e., that no subgroup is discriminated against. It is known that ensuring \emph{marginal fairness} for every dimension independently is not sufficient in general. Due to the exponential number of subgroups, however, directly measuring intersectional fairness from data is impossible. In this paper, our primary goal is to understand in detail the relationship between marginal and intersectional fairness through statistical analysis. We first identify a set of sufficient conditions under which an exact relationship can be obtained. Then, we prove bounds (easily computable through marginal fairness and other meaningful statistical quantities) in high-probability on intersectional fairness in the general case. Beyond their descriptive value, we show that these theoretical bounds can be leveraged to derive a heuristic improving the approximation and bounds of intersectional fairness by choosing, in a relevant manner, protected attributes for which we describe intersectional subgroups. Finally, we test the performance of our approximations and bounds on real and synthetic data-sets.

Static Scheduling with Predictions Learned through Efficient Exploration

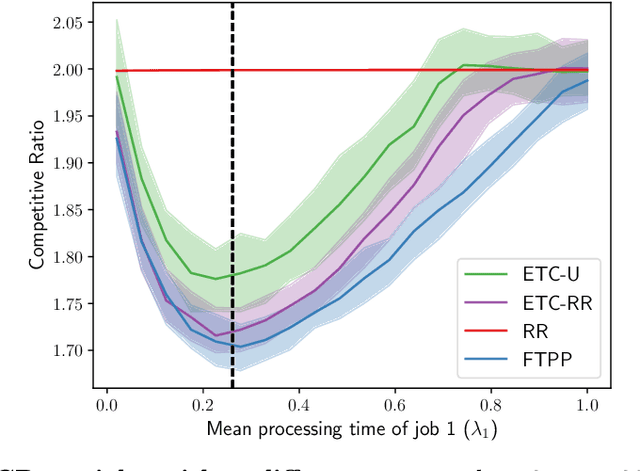
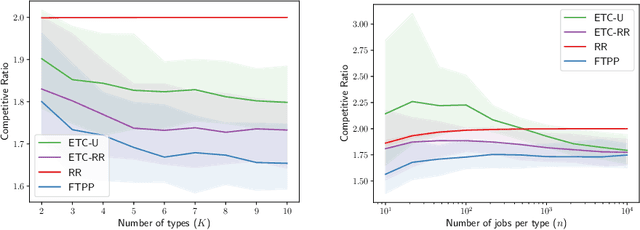
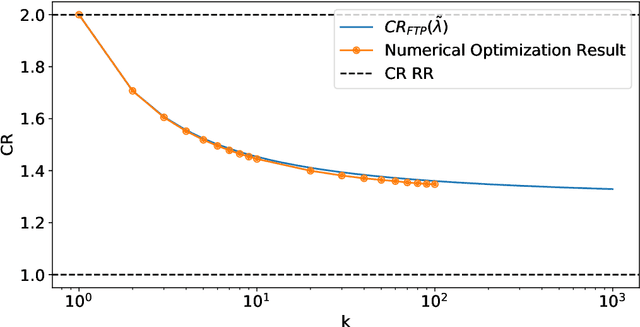
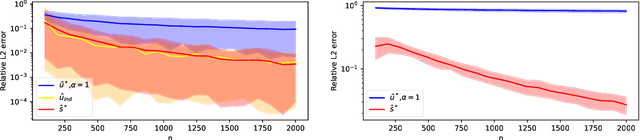
A popular approach to go beyond the worst-case analysis of online algorithms is to assume the existence of predictions that can be leveraged to improve performances. Those predictions are usually given by some external sources that cannot be fully trusted. Instead, we argue that trustful predictions can be built by algorithms, while they run. We investigate this idea in the illustrative context of static scheduling with exponential job sizes. Indeed, we prove that algorithms agnostic to this structure do not perform better than in the worst case. In contrast, when the expected job sizes are known, we show that the best algorithm using this information, called Follow-The-Perfect-Prediction (FTPP), exhibits much better performances. Then, we introduce two adaptive explore-then-commit types of algorithms: they both first (partially) learn expected job sizes and then follow FTPP once their self-predictions are confident enough. On the one hand, ETCU explores in "series", by completing jobs sequentially to acquire information. On the other hand, ETCRR, inspired by the optimal worst-case algorithm Round-Robin (RR), explores efficiently in "parallel". We prove that both of them asymptotically reach the performances of FTPP, with a faster rate for ETCRR. Those findings are empirically evaluated on synthetic data.