Model Predictive Control is Almost Optimal for Restless Bandit

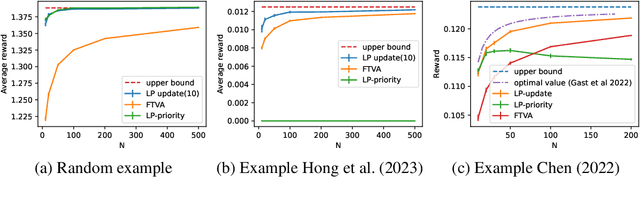
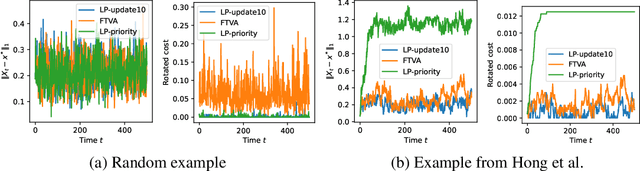
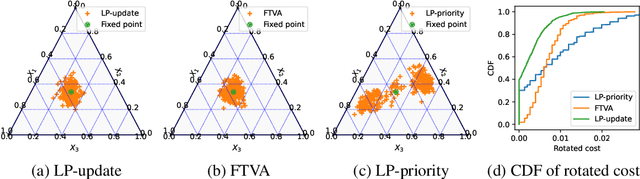
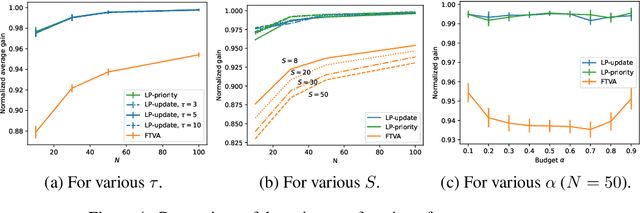
We consider the discrete time infinite horizon average reward restless markovian bandit (RMAB) problem. We propose a \emph{model predictive control} based non-stationary policy with a rolling computational horizon $\tau$. At each time-slot, this policy solves a $\tau$ horizon linear program whose first control value is kept as a control for the RMAB. Our solution requires minimal assumptions and quantifies the loss in optimality in terms of $\tau$ and the number of arms, $N$. We show that its sub-optimality gap is $O(1/\sqrt{N})$ in general, and $\exp(-\Omega(N))$ under a local-stability condition. Our proof is based on a framework from dynamic control known as \emph{dissipativity}. Our solution easy to implement and performs very well in practice when compared to the state of the art. Further, both our solution and our proof methodology can easily be generalized to more general constrained MDP settings and should thus, be of great interest to the burgeoning RMAB community.

Computing the Bias of Constant-step Stochastic Approximation with Markovian Noise

We study stochastic approximation algorithms with Markovian noise and constant step-size $\alpha$. We develop a method based on infinitesimal generator comparisons to study the bias of the algorithm, which is the expected difference between $\theta_n$ -- the value at iteration $n$ -- and $\theta^*$ -- the unique equilibrium of the corresponding ODE. We show that, under some smoothness conditions, this bias is of order $O(\alpha)$. Furthermore, we show that the time-averaged bias is equal to $\alpha V + O(\alpha^2)$, where $V$ is a constant characterized by a Lyapunov equation, showing that $\esp{\bar{\theta}_n} \approx \theta^*+V\alpha + O(\alpha^2)$, where $\bar{\theta}_n=(1/n)\sum_{k=1}^n\theta_k$ is the Polyak-Ruppert average. We also show that $\bar{\theta}_n$ converges with high probability around $\theta^*+\alpha V$. We illustrate how to combine this with Richardson-Romberg extrapolation to derive an iterative scheme with a bias of order $O(\alpha^2)$.

Trading-off price for data quality to achieve fair online allocation

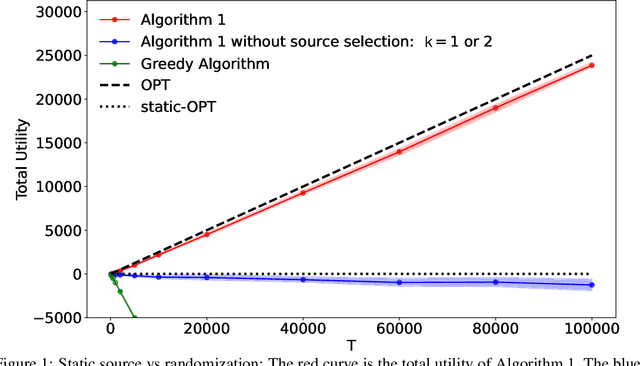
We consider the problem of online allocation subject to a long-term fairness penalty. Contrary to existing works, however, we do not assume that the decision-maker observes the protected attributes -- which is often unrealistic in practice. Instead they can purchase data that help estimate them from sources of different quality; and hence reduce the fairness penalty at some cost. We model this problem as a multi-armed bandit problem where each arm corresponds to the choice of a data source, coupled with the online allocation problem. We propose an algorithm that jointly solves both problems and show that it has a regret bounded by $\mathcal{O}(\sqrt{T})$. A key difficulty is that the rewards received by selecting a source are correlated by the fairness penalty, which leads to a need for randomization (despite a stochastic setting). Our algorithm takes into account contextual information available before the source selection, and can adapt to many different fairness notions. We also show that in some instances, the estimates used can be learned on the fly.

Decentralized model-free reinforcement learning in stochastic games with average-reward objective

We propose the first model-free algorithm that achieves low regret performance for decentralized learning in two-player zero-sum tabular stochastic games with infinite-horizon average-reward objective. In decentralized learning, the learning agent controls only one player and tries to achieve low regret performances against an arbitrary opponent. This contrasts with centralized learning where the agent tries to approximate the Nash equilibrium by controlling both players. In our infinite-horizon undiscounted setting, additional structure assumptions is needed to provide good behaviors of learning processes : here we assume for every strategy of the opponent, the agent has a way to go from any state to any other. This assumption is the analogous to the "communicating" assumption in the MDP setting. We show that our Decentralized Optimistic Nash Q-Learning (DONQ-learning) algorithm achieves both sublinear high probability regret of order $T^{3/4}$ and sublinear expected regret of order $T^{2/3}$. Moreover, our algorithm enjoys a low computational complexity and low memory space requirement compared to the previous works of (Wei et al. 2017) and (Jafarnia-Jahromi et al. 2021) in the same setting.

On Fair Selection in the Presence of Implicit and Differential Variance

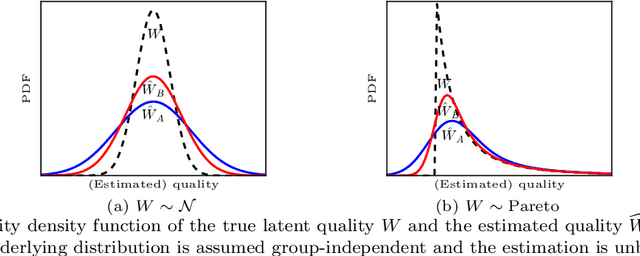
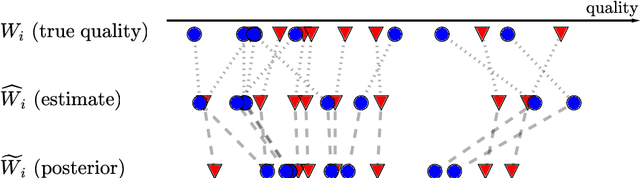
Discrimination in selection problems such as hiring or college admission is often explained by implicit bias from the decision maker against disadvantaged demographic groups. In this paper, we consider a model where the decision maker receives a noisy estimate of each candidate's quality, whose variance depends on the candidate's group -- we argue that such differential variance is a key feature of many selection problems. We analyze two notable settings: in the first, the noise variances are unknown to the decision maker who simply picks the candidates with the highest estimated quality independently of their group; in the second, the variances are known and the decision maker picks candidates having the highest expected quality given the noisy estimate. We show that both baseline decision makers yield discrimination, although in opposite directions: the first leads to underrepresentation of the low-variance group while the second leads to underrepresentation of the high-variance group. We study the effect on the selection utility of imposing a fairness mechanism that we term the $\gamma$-rule (it is an extension of the classical four-fifths rule and it also includes demographic parity). In the first setting (with unknown variances), we prove that under mild conditions, imposing the $\gamma$-rule increases the selection utility -- here there is no trade-off between fairness and utility. In the second setting (with known variances), imposing the $\gamma$-rule decreases the utility but we prove a bound on the utility loss due to the fairness mechanism.

Reinforcement Learning for Markovian Bandits: Is Posterior Sampling more Scalable than Optimism?

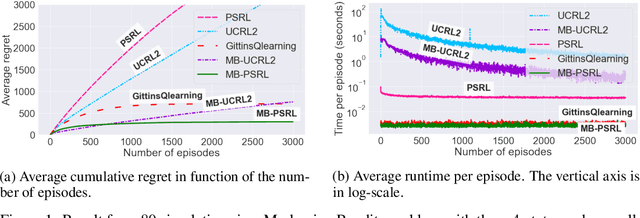
We study learning algorithms for the classical Markovian bandit problem with discount. We explain how to adapt PSRL [24] and UCRL2 [2] to exploit the problem structure. These variants are called MB-PSRL and MB-UCRL2. While the regret bound and runtime of vanilla implementations of PSRL and UCRL2 are exponential in the number of bandits, we show that the episodic regret of MB-PSRL and MB-UCRL2 is $\tilde O(S\sqrt{nK})$ where $K$ is the number of episodes, n is the number of bandits and S is the number of states of each bandit (the exact bound in $S$, $n$ and $K$ is given in the paper). Up to a factor $\sqrt S$, this matches the lower bound of $\Omega(\sqrt{SnK}$) that we also derive in the paper. MB-PSRL is also computationally efficient: its runtime is linear in the number of bandits. We further show that this linear runtime cannot be achieved by adapting classical non-Bayesian algorithms such as UCRL2 or UCBVI to Markovian bandit problems. Finally, we perform numerical experiments that confirm that MB-PSRL outperforms other existing algorithms in practice, both in terms of regret and of computation time.

On Fair Selection in the Presence of Implicit Variance

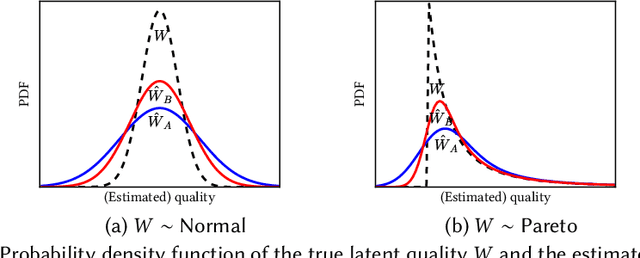
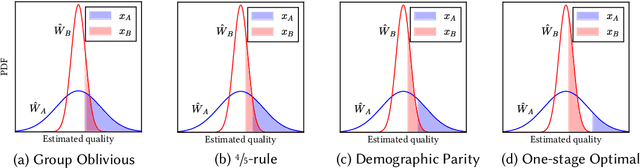
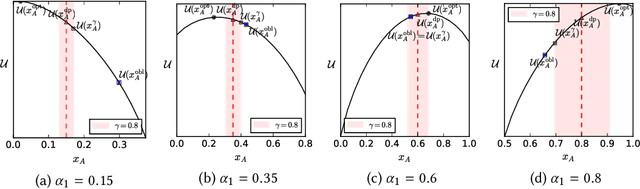
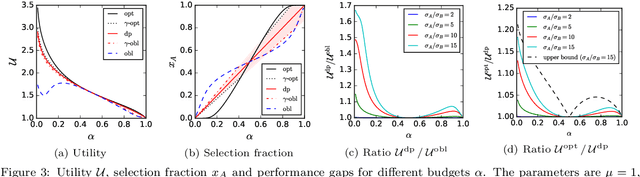
Quota-based fairness mechanisms like the so-called Rooney rule or four-fifths rule are used in selection problems such as hiring or college admission to reduce inequalities based on sensitive demographic attributes. These mechanisms are often viewed as introducing a trade-off between selection fairness and utility. In recent work, however, Kleinberg and Raghavan showed that, in the presence of implicit bias in estimating candidates' quality, the Rooney rule can increase the utility of the selection process. We argue that even in the absence of implicit bias, the estimates of candidates' quality from different groups may differ in another fundamental way, namely, in their variance. We term this phenomenon implicit variance and we ask: can fairness mechanisms be beneficial to the utility of a selection process in the presence of implicit variance (even in the absence of implicit bias)? To answer this question, we propose a simple model in which candidates have a true latent quality that is drawn from a group-independent normal distribution. To make the selection, a decision maker receives an unbiased estimate of the quality of each candidate, with normal noise, but whose variance depends on the candidate's group. We then compare the utility obtained by imposing a fairness mechanism that we term $\gamma$-rule (it includes demographic parity and the four-fifths rule as special cases), to that of a group-oblivious selection algorithm that picks the candidates with the highest estimated quality independently of their group. Our main result shows that the demographic parity mechanism always increases the selection utility, while any $\gamma$-rule weakly increases it. We extend our model to a two-stage selection process where the true quality is observed at the second stage. We discuss multiple extensions of our results, in particular to different distributions of the true latent quality.

The Price of Local Fairness in Multistage Selection

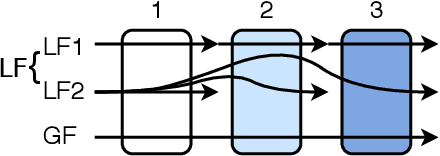
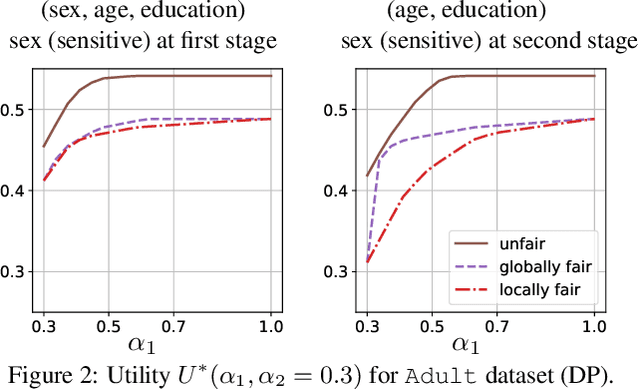
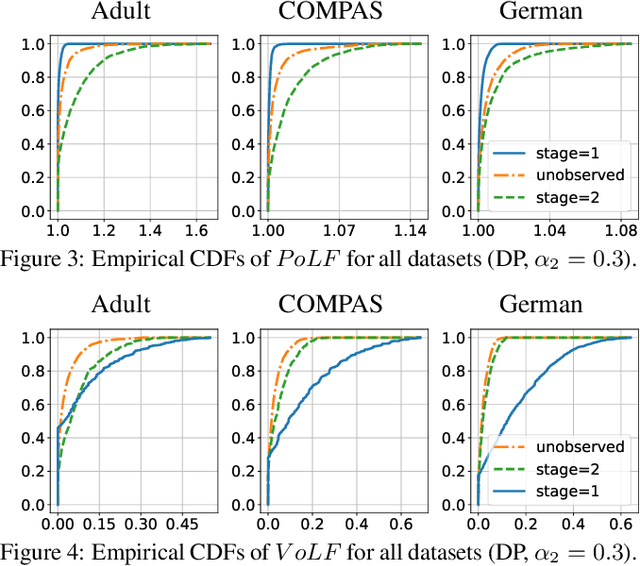
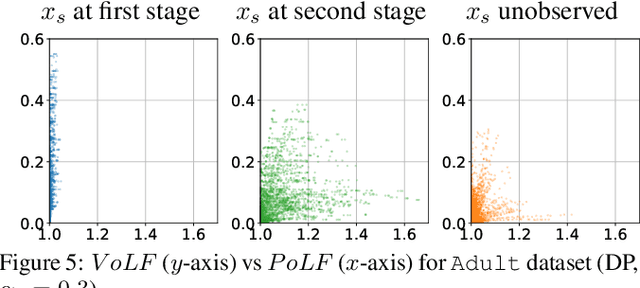
The rise of algorithmic decision making led to active researches on how to define and guarantee fairness, mostly focusing on one-shot decision making. In several important applications such as hiring, however, decisions are made in multiple stage with additional information at each stage. In such cases, fairness issues remain poorly understood. In this paper we study fairness in $k$-stage selection problems where additional features are observed at every stage. We first introduce two fairness notions, local (per stage) and global (final stage) fairness, that extend the classical fairness notions to the $k$-stage setting. We propose a simple model based on a probabilistic formulation and show that the locally and globally fair selections that maximize precision can be computed via a linear program. We then define the price of local fairness to measure the loss of precision induced by local constraints; and investigate theoretically and empirically this quantity. In particular, our experiments show that the price of local fairness is generally smaller when the sensitive attribute is observed at the first stage; but globally fair selections are more locally fair when the sensitive attribute is observed at the second stage---hence in both cases it is often possible to have a selection that has a small price of local fairness and is close to locally fair.

Mean field for Markov Decision Processes: from Discrete to Continuous Optimization

We study the convergence of Markov Decision Processes made of a large number of objects to optimization problems on ordinary differential equations (ODE). We show that the optimal reward of such a Markov Decision Process, satisfying a Bellman equation, converges to the solution of a continuous Hamilton-Jacobi-Bellman (HJB) equation based on the mean field approximation of the Markov Decision Process. We give bounds on the difference of the rewards, and a constructive algorithm for deriving an approximating solution to the Markov Decision Process from a solution of the HJB equations. We illustrate the method on three examples pertaining respectively to investment strategies, population dynamics control and scheduling in queues are developed. They are used to illustrate and justify the construction of the controlled ODE and to show the gain obtained by solving a continuous HJB equation rather than a large discrete Bellman equation.