PITA: Preference-Guided Inference-Time Alignment for LLM Post-Training

Inference-time alignment enables large language models (LLMs) to generate outputs aligned with end-user preferences without further training. Recent post-training methods achieve this by using small guidance models to modify token generation during inference. These methods typically optimize a reward function KL-regularized by the original LLM taken as the reference policy. A critical limitation, however, is their dependence on a pre-trained reward model, which requires fitting to human preference feedback--a potentially unstable process. In contrast, we introduce PITA, a novel framework that integrates preference feedback directly into the LLM's token generation, eliminating the need for a reward model. PITA learns a small preference-based guidance policy to modify token probabilities at inference time without LLM fine-tuning, reducing computational cost and bypassing the pre-trained reward model dependency. The problem is framed as identifying an underlying preference distribution, solved through stochastic search and iterative refinement of the preference-based guidance model. We evaluate PITA across diverse tasks, including mathematical reasoning and sentiment classification, demonstrating its effectiveness in aligning LLM outputs with user preferences.

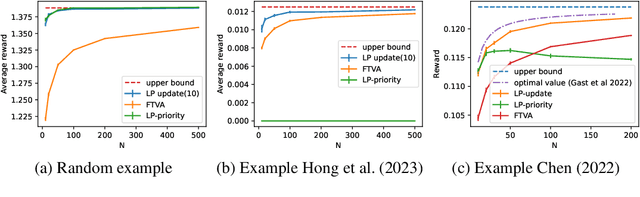
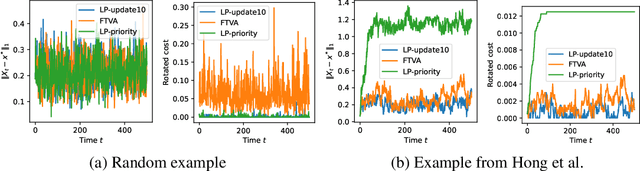
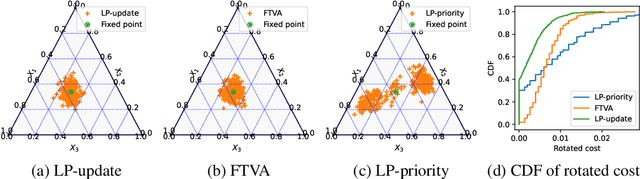
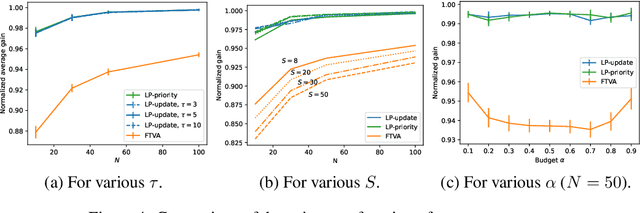
Model Predictive Control is Almost Optimal for Restless Bandit

We consider the discrete time infinite horizon average reward restless markovian bandit (RMAB) problem. We propose a \emph{model predictive control} based non-stationary policy with a rolling computational horizon $\tau$. At each time-slot, this policy solves a $\tau$ horizon linear program whose first control value is kept as a control for the RMAB. Our solution requires minimal assumptions and quantifies the loss in optimality in terms of $\tau$ and the number of arms, $N$. We show that its sub-optimality gap is $O(1/\sqrt{N})$ in general, and $\exp(-\Omega(N))$ under a local-stability condition. Our proof is based on a framework from dynamic control known as \emph{dissipativity}. Our solution easy to implement and performs very well in practice when compared to the state of the art. Further, both our solution and our proof methodology can easily be generalized to more general constrained MDP settings and should thus, be of great interest to the burgeoning RMAB community.

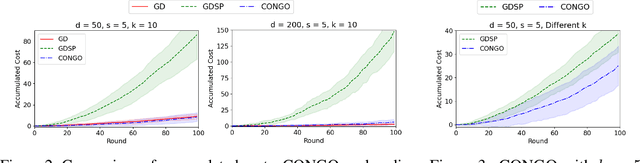
CONGO: Compressive Online Gradient Optimization with Application to Microservices Management

We address the challenge of online convex optimization where the objective function's gradient exhibits sparsity, indicating that only a small number of dimensions possess non-zero gradients. Our aim is to leverage this sparsity to obtain useful estimates of the objective function's gradient even when the only information available is a limited number of function samples. Our motivation stems from distributed queueing systems like microservices-based applications, characterized by request-response workloads. Here, each request type proceeds through a sequence of microservices to produce a response, and the resource allocation across the collection of microservices is controlled to balance end-to-end latency with resource costs. While the number of microservices is substantial, the latency function primarily reacts to resource changes in a few, rendering the gradient sparse. Our proposed method, CONGO (Compressive Online Gradient Optimization), combines simultaneous perturbation with compressive sensing to estimate gradients. We establish analytical bounds on the requisite number of compressive sensing samples per iteration to maintain bounded bias of gradient estimates, ensuring sub-linear regret. By exploiting sparsity, we reduce the samples required per iteration to match the gradient's sparsity, rather than the problem's original dimensionality. Numerical experiments and real-world microservices benchmarks demonstrate CONGO's superiority over multiple stochastic gradient descent approaches, as it quickly converges to performance comparable to policies pre-trained with workload awareness.