On Fair Selection in the Presence of Implicit Variance

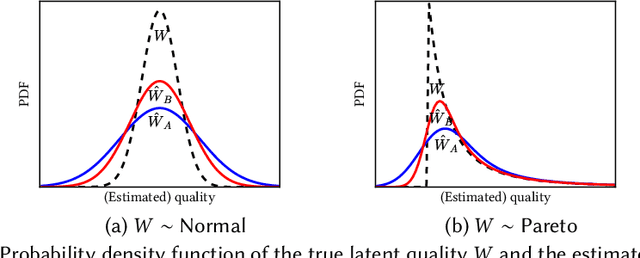
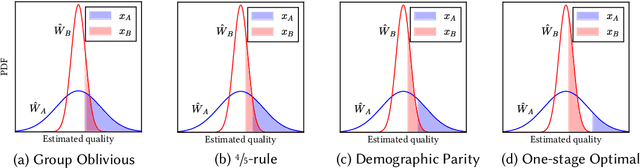
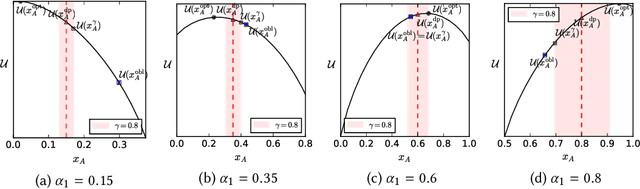
Quota-based fairness mechanisms like the so-called Rooney rule or four-fifths rule are used in selection problems such as hiring or college admission to reduce inequalities based on sensitive demographic attributes. These mechanisms are often viewed as introducing a trade-off between selection fairness and utility. In recent work, however, Kleinberg and Raghavan showed that, in the presence of implicit bias in estimating candidates' quality, the Rooney rule can increase the utility of the selection process. We argue that even in the absence of implicit bias, the estimates of candidates' quality from different groups may differ in another fundamental way, namely, in their variance. We term this phenomenon implicit variance and we ask: can fairness mechanisms be beneficial to the utility of a selection process in the presence of implicit variance (even in the absence of implicit bias)? To answer this question, we propose a simple model in which candidates have a true latent quality that is drawn from a group-independent normal distribution. To make the selection, a decision maker receives an unbiased estimate of the quality of each candidate, with normal noise, but whose variance depends on the candidate's group. We then compare the utility obtained by imposing a fairness mechanism that we term $\gamma$-rule (it includes demographic parity and the four-fifths rule as special cases), to that of a group-oblivious selection algorithm that picks the candidates with the highest estimated quality independently of their group. Our main result shows that the demographic parity mechanism always increases the selection utility, while any $\gamma$-rule weakly increases it. We extend our model to a two-stage selection process where the true quality is observed at the second stage. We discuss multiple extensions of our results, in particular to different distributions of the true latent quality.