Logarithmic Regret of Exploration in Average Reward Markov Decision Processes

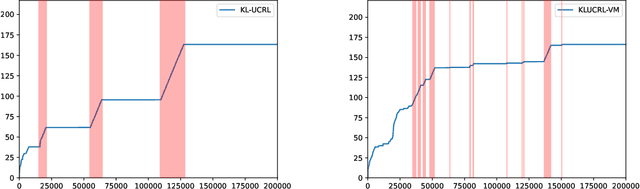
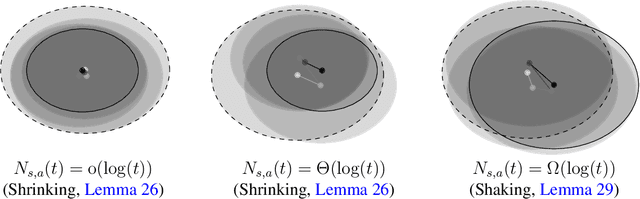
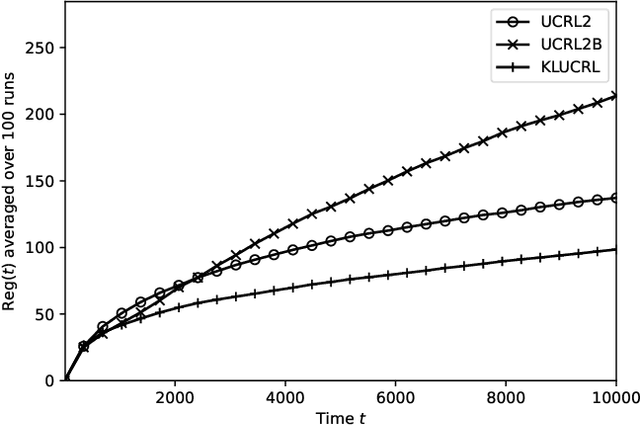
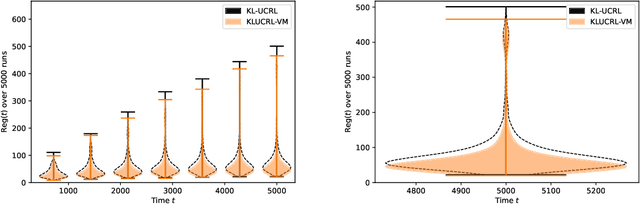
In average reward Markov decision processes, state-of-the-art algorithms for regret minimization follow a well-established framework: They are model-based, optimistic and episodic. First, they maintain a confidence region from which optimistic policies are computed using a well-known subroutine called Extended Value Iteration (EVI). Second, these policies are used over time windows called episodes, each ended by the Doubling Trick (DT) rule or a variant thereof. In this work, without modifying EVI, we show that there is a significant advantage in replacing (DT) by another simple rule, that we call the Vanishing Multiplicative (VM) rule. When managing episodes with (VM), the algorithm's regret is, both in theory and in practice, as good if not better than with (DT), while the one-shot behavior is greatly improved. More specifically, the management of bad episodes (when sub-optimal policies are being used) is much better under (VM) than (DT) by making the regret of exploration logarithmic rather than linear. These results are made possible by a new in-depth understanding of the contrasting behaviors of confidence regions during good and bad episodes.

Learning Optimal Admission Control in Partially Observable Queueing Networks

We present an efficient reinforcement learning algorithm that learns the optimal admission control policy in a partially observable queueing network. Specifically, only the arrival and departure times from the network are observable, and optimality refers to the average holding/rejection cost in infinite horizon. While reinforcement learning in Partially Observable Markov Decision Processes (POMDP) is prohibitively expensive in general, we show that our algorithm has a regret that only depends sub-linearly on the maximal number of jobs in the network, $S$. In particular, in contrast with existing regret analyses, our regret bound does not depend on the diameter of the underlying Markov Decision Process (MDP), which in most queueing systems is at least exponential in $S$. The novelty of our approach is to leverage Norton's equivalent theorem for closed product-form queueing networks and an efficient reinforcement learning algorithm for MDPs with the structure of birth-and-death processes.

Reinforcement Learning in a Birth and Death Process: Breaking the Dependence on the State Space

In this paper, we revisit the regret of undiscounted reinforcement learning in MDPs with a birth and death structure. Specifically, we consider a controlled queue with impatient jobs and the main objective is to optimize a trade-off between energy consumption and user-perceived performance. Within this setting, the \emph{diameter} $D$ of the MDP is $\Omega(S^S)$, where $S$ is the number of states. Therefore, the existing lower and upper bounds on the regret at time$T$, of order $O(\sqrt{DSAT})$ for MDPs with $S$ states and $A$ actions, may suggest that reinforcement learning is inefficient here. In our main result however, we exploit the structure of our MDPs to show that the regret of a slightly-tweaked version of the classical learning algorithm {\sc Ucrl2} is in fact upper bounded by $\tilde{\mathcal{O}}(\sqrt{E_2AT})$ where $E_2$ is related to the weighted second moment of the stationary measure of a reference policy. Importantly, $E_2$ is bounded independently of $S$. Thus, our bound is asymptotically independent of the number of states and of the diameter. This result is based on a careful study of the number of visits performed by the learning algorithm to the states of the MDP, which is highly non-uniform.

Decentralized model-free reinforcement learning in stochastic games with average-reward objective

We propose the first model-free algorithm that achieves low regret performance for decentralized learning in two-player zero-sum tabular stochastic games with infinite-horizon average-reward objective. In decentralized learning, the learning agent controls only one player and tries to achieve low regret performances against an arbitrary opponent. This contrasts with centralized learning where the agent tries to approximate the Nash equilibrium by controlling both players. In our infinite-horizon undiscounted setting, additional structure assumptions is needed to provide good behaviors of learning processes : here we assume for every strategy of the opponent, the agent has a way to go from any state to any other. This assumption is the analogous to the "communicating" assumption in the MDP setting. We show that our Decentralized Optimistic Nash Q-Learning (DONQ-learning) algorithm achieves both sublinear high probability regret of order $T^{3/4}$ and sublinear expected regret of order $T^{2/3}$. Moreover, our algorithm enjoys a low computational complexity and low memory space requirement compared to the previous works of (Wei et al. 2017) and (Jafarnia-Jahromi et al. 2021) in the same setting.

Reinforcement Learning for Markovian Bandits: Is Posterior Sampling more Scalable than Optimism?

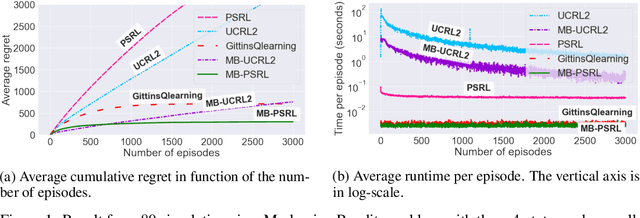
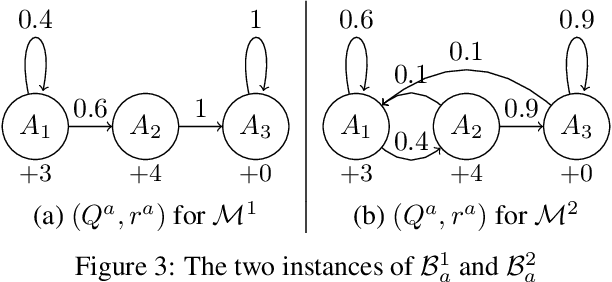
We study learning algorithms for the classical Markovian bandit problem with discount. We explain how to adapt PSRL [24] and UCRL2 [2] to exploit the problem structure. These variants are called MB-PSRL and MB-UCRL2. While the regret bound and runtime of vanilla implementations of PSRL and UCRL2 are exponential in the number of bandits, we show that the episodic regret of MB-PSRL and MB-UCRL2 is $\tilde O(S\sqrt{nK})$ where $K$ is the number of episodes, n is the number of bandits and S is the number of states of each bandit (the exact bound in $S$, $n$ and $K$ is given in the paper). Up to a factor $\sqrt S$, this matches the lower bound of $\Omega(\sqrt{SnK}$) that we also derive in the paper. MB-PSRL is also computationally efficient: its runtime is linear in the number of bandits. We further show that this linear runtime cannot be achieved by adapting classical non-Bayesian algorithms such as UCRL2 or UCBVI to Markovian bandit problems. Finally, we perform numerical experiments that confirm that MB-PSRL outperforms other existing algorithms in practice, both in terms of regret and of computation time.

Penalty-regulated dynamics and robust learning procedures in games

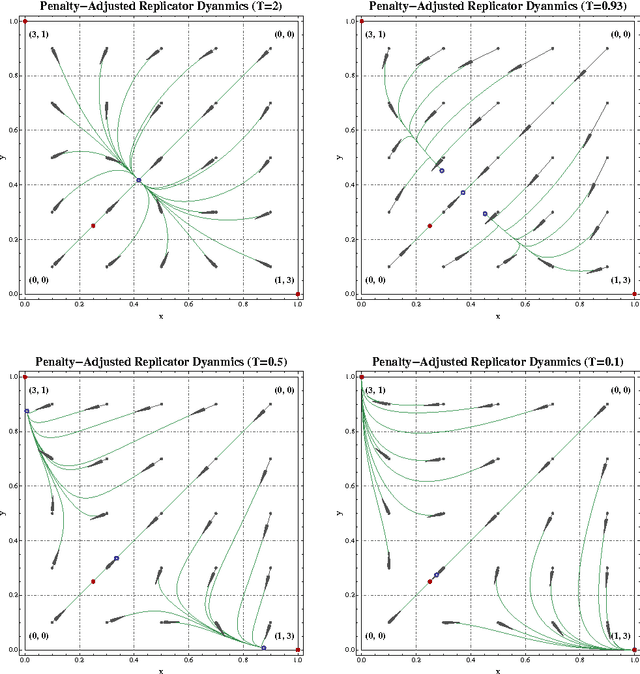
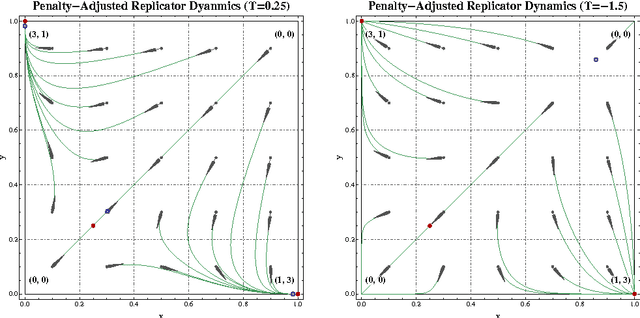
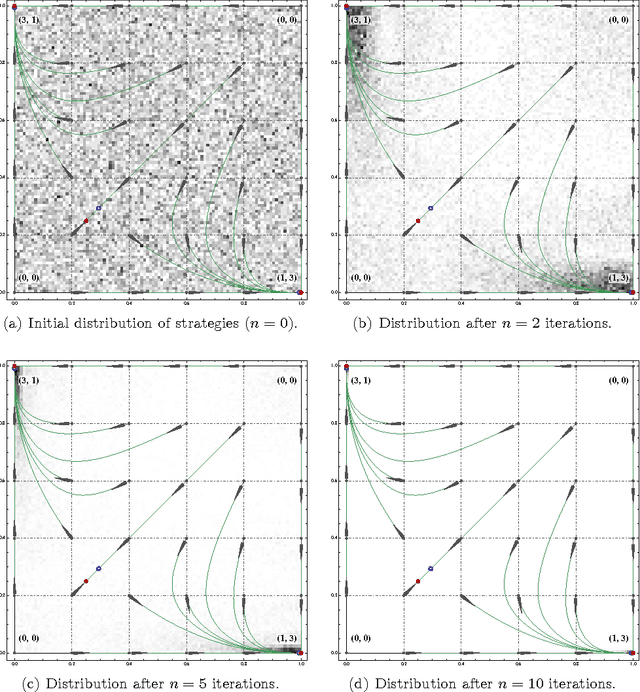
Starting from a heuristic learning scheme for N-person games, we derive a new class of continuous-time learning dynamics consisting of a replicator-like drift adjusted by a penalty term that renders the boundary of the game's strategy space repelling. These penalty-regulated dynamics are equivalent to players keeping an exponentially discounted aggregate of their on-going payoffs and then using a smooth best response to pick an action based on these performance scores. Owing to this inherent duality, the proposed dynamics satisfy a variant of the folk theorem of evolutionary game theory and they converge to (arbitrarily precise) approximations of Nash equilibria in potential games. Motivated by applications to traffic engineering, we exploit this duality further to design a discrete-time, payoff-based learning algorithm which retains these convergence properties and only requires players to observe their in-game payoffs: moreover, the algorithm remains robust in the presence of stochastic perturbations and observation errors, and it does not require any synchronization between players.

Mean field for Markov Decision Processes: from Discrete to Continuous Optimization

We study the convergence of Markov Decision Processes made of a large number of objects to optimization problems on ordinary differential equations (ODE). We show that the optimal reward of such a Markov Decision Process, satisfying a Bellman equation, converges to the solution of a continuous Hamilton-Jacobi-Bellman (HJB) equation based on the mean field approximation of the Markov Decision Process. We give bounds on the difference of the rewards, and a constructive algorithm for deriving an approximating solution to the Markov Decision Process from a solution of the HJB equations. We illustrate the method on three examples pertaining respectively to investment strategies, population dynamics control and scheduling in queues are developed. They are used to illustrate and justify the construction of the controlled ODE and to show the gain obtained by solving a continuous HJB equation rather than a large discrete Bellman equation.