Logarithmic Regret of Exploration in Average Reward Markov Decision Processes
Paper and Code
Feb 10, 2025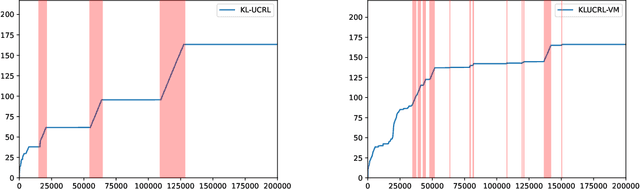
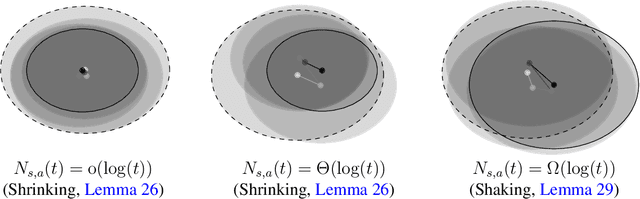
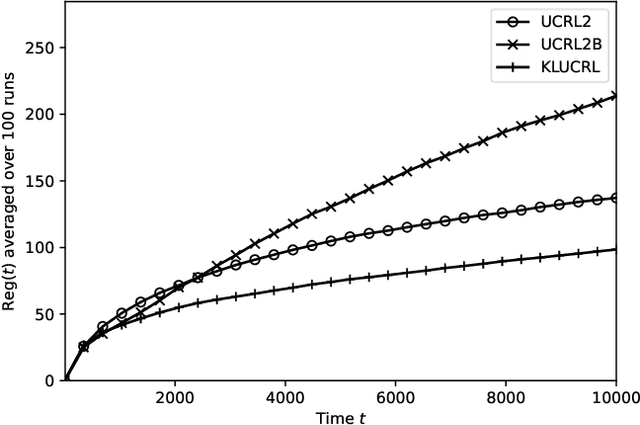
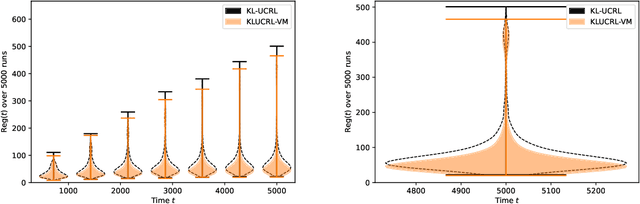
In average reward Markov decision processes, state-of-the-art algorithms for regret minimization follow a well-established framework: They are model-based, optimistic and episodic. First, they maintain a confidence region from which optimistic policies are computed using a well-known subroutine called Extended Value Iteration (EVI). Second, these policies are used over time windows called episodes, each ended by the Doubling Trick (DT) rule or a variant thereof. In this work, without modifying EVI, we show that there is a significant advantage in replacing (DT) by another simple rule, that we call the Vanishing Multiplicative (VM) rule. When managing episodes with (VM), the algorithm's regret is, both in theory and in practice, as good if not better than with (DT), while the one-shot behavior is greatly improved. More specifically, the management of bad episodes (when sub-optimal policies are being used) is much better under (VM) than (DT) by making the regret of exploration logarithmic rather than linear. These results are made possible by a new in-depth understanding of the contrasting behaviors of confidence regions during good and bad episodes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge