Kimang Khun
POLARIS
Reinforcement Learning for Markovian Bandits: Is Posterior Sampling more Scalable than Optimism?
Jun 16, 2021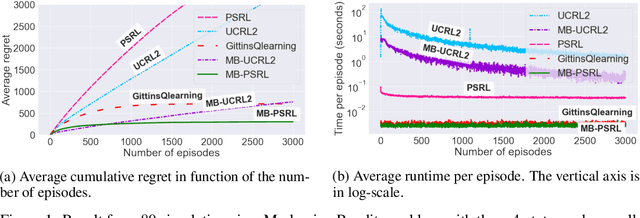


Abstract:We study learning algorithms for the classical Markovian bandit problem with discount. We explain how to adapt PSRL [24] and UCRL2 [2] to exploit the problem structure. These variants are called MB-PSRL and MB-UCRL2. While the regret bound and runtime of vanilla implementations of PSRL and UCRL2 are exponential in the number of bandits, we show that the episodic regret of MB-PSRL and MB-UCRL2 is $\tilde O(S\sqrt{nK})$ where $K$ is the number of episodes, n is the number of bandits and S is the number of states of each bandit (the exact bound in $S$, $n$ and $K$ is given in the paper). Up to a factor $\sqrt S$, this matches the lower bound of $\Omega(\sqrt{SnK}$) that we also derive in the paper. MB-PSRL is also computationally efficient: its runtime is linear in the number of bandits. We further show that this linear runtime cannot be achieved by adapting classical non-Bayesian algorithms such as UCRL2 or UCBVI to Markovian bandit problems. Finally, we perform numerical experiments that confirm that MB-PSRL outperforms other existing algorithms in practice, both in terms of regret and of computation time.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge