Penalty-regulated dynamics and robust learning procedures in games
Paper and Code
Apr 06, 2014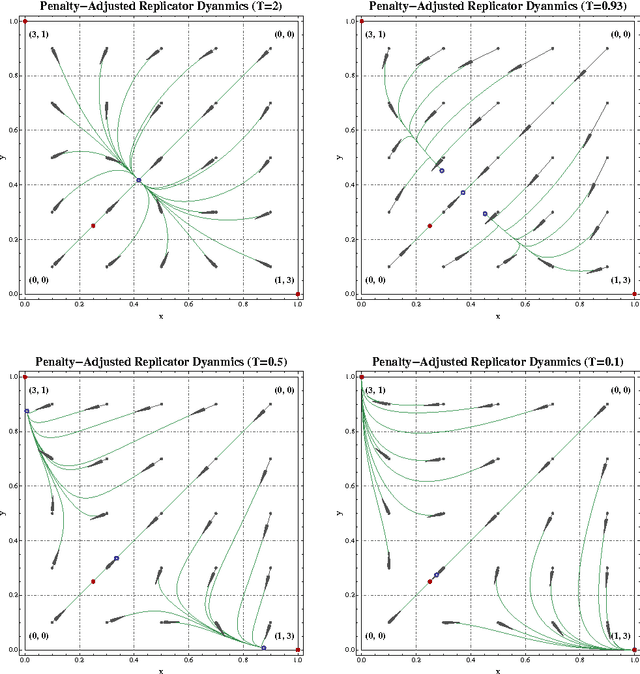

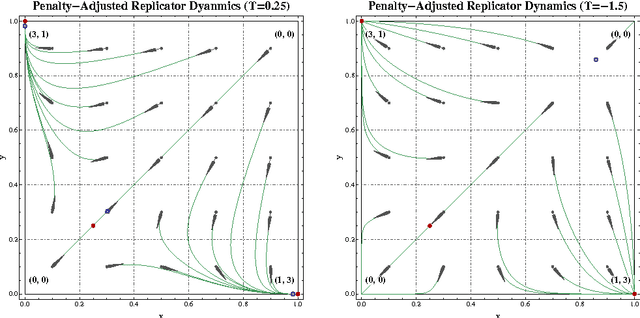
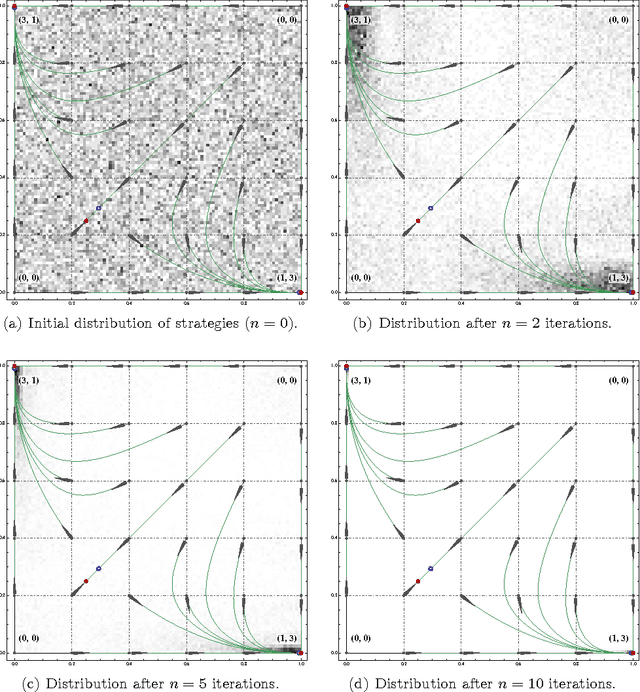
Starting from a heuristic learning scheme for N-person games, we derive a new class of continuous-time learning dynamics consisting of a replicator-like drift adjusted by a penalty term that renders the boundary of the game's strategy space repelling. These penalty-regulated dynamics are equivalent to players keeping an exponentially discounted aggregate of their on-going payoffs and then using a smooth best response to pick an action based on these performance scores. Owing to this inherent duality, the proposed dynamics satisfy a variant of the folk theorem of evolutionary game theory and they converge to (arbitrarily precise) approximations of Nash equilibria in potential games. Motivated by applications to traffic engineering, we exploit this duality further to design a discrete-time, payoff-based learning algorithm which retains these convergence properties and only requires players to observe their in-game payoffs: moreover, the algorithm remains robust in the presence of stochastic perturbations and observation errors, and it does not require any synchronization between players.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge