Krishna Gummadi
Lawma: The Power of Specialization for Legal Tasks
Jul 23, 2024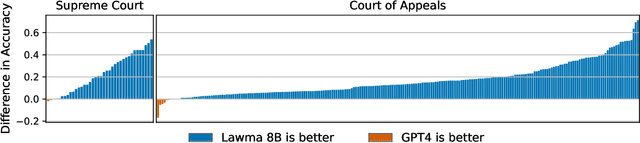


Abstract:Annotation and classification of legal text are central components of empirical legal research. Traditionally, these tasks are often delegated to trained research assistants. Motivated by the advances in language modeling, empirical legal scholars are increasingly turning to prompting commercial models, hoping that it will alleviate the significant cost of human annotation. Despite growing use, our understanding of how to best utilize large language models for legal tasks remains limited. We conduct a comprehensive study of 260 legal text classification tasks, nearly all new to the machine learning community. Starting from GPT-4 as a baseline, we show that it has non-trivial but highly varied zero-shot accuracy, often exhibiting performance that may be insufficient for legal work. We then demonstrate that a lightly fine-tuned Llama 3 model vastly outperforms GPT-4 on almost all tasks, typically by double-digit percentage points. We find that larger models respond better to fine-tuning than smaller models. A few tens to hundreds of examples suffice to achieve high classification accuracy. Notably, we can fine-tune a single model on all 260 tasks simultaneously at a small loss in accuracy relative to having a separate model for each task. Our work points to a viable alternative to the predominant practice of prompting commercial models. For concrete legal tasks with some available labeled data, researchers are better off using a fine-tuned open-source model.
The Price of Local Fairness in Multistage Selection
Jun 15, 2019
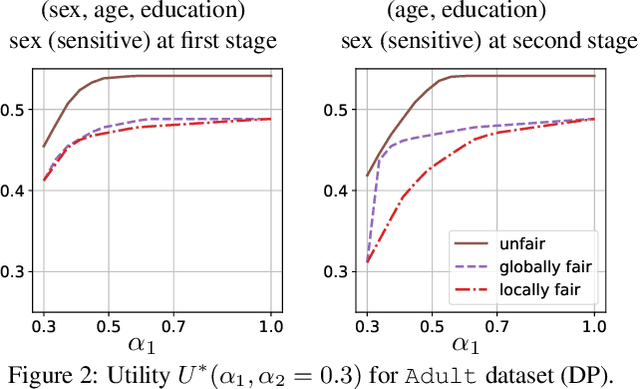
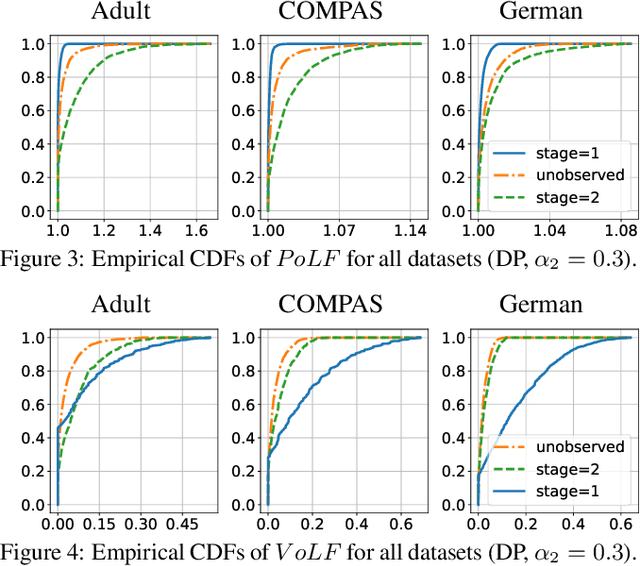
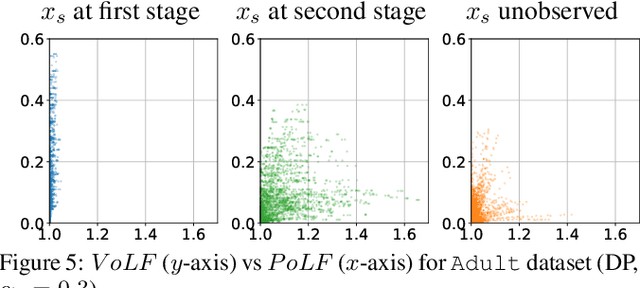
Abstract:The rise of algorithmic decision making led to active researches on how to define and guarantee fairness, mostly focusing on one-shot decision making. In several important applications such as hiring, however, decisions are made in multiple stage with additional information at each stage. In such cases, fairness issues remain poorly understood. In this paper we study fairness in $k$-stage selection problems where additional features are observed at every stage. We first introduce two fairness notions, local (per stage) and global (final stage) fairness, that extend the classical fairness notions to the $k$-stage setting. We propose a simple model based on a probabilistic formulation and show that the locally and globally fair selections that maximize precision can be computed via a linear program. We then define the price of local fairness to measure the loss of precision induced by local constraints; and investigate theoretically and empirically this quantity. In particular, our experiments show that the price of local fairness is generally smaller when the sensitive attribute is observed at the first stage; but globally fair selections are more locally fair when the sensitive attribute is observed at the second stage---hence in both cases it is often possible to have a selection that has a small price of local fairness and is close to locally fair.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge