Almost Free: Self-concordance in Natural Exponential Families and an Application to Bandits

We prove that single-parameter natural exponential families with subexponential tails are self-concordant with polynomial-sized parameters. For subgaussian natural exponential families we establish an exact characterization of the growth rate of the self-concordance parameter. Applying these findings to bandits allows us to fill gaps in the literature: We show that optimistic algorithms for generalized linear bandits enjoy regret bounds that are both second-order (scale with the variance of the optimal arm's reward distribution) and free of an exponential dependence on the bound of the problem parameter in the leading term. To the best of our knowledge, ours is the first regret bound for generalized linear bandits with subexponential tails, broadening the class of problems to include Poisson, exponential and gamma bandits.

Static Scheduling with Predictions Learned through Efficient Exploration

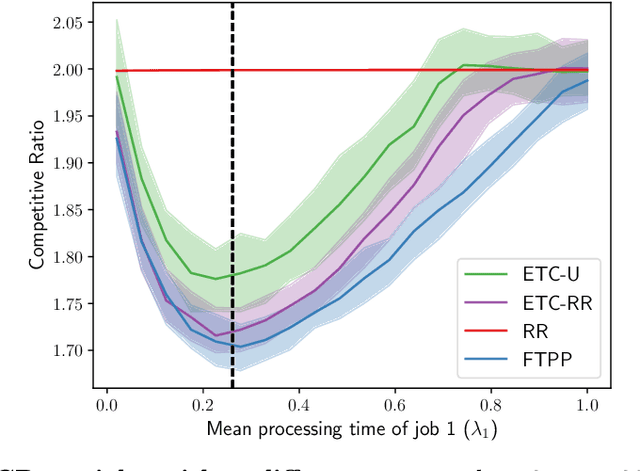
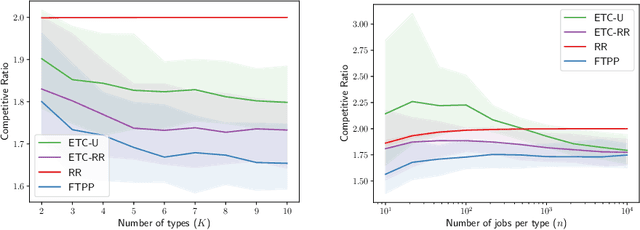
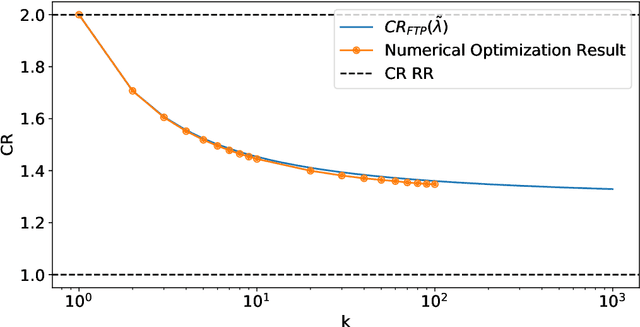
A popular approach to go beyond the worst-case analysis of online algorithms is to assume the existence of predictions that can be leveraged to improve performances. Those predictions are usually given by some external sources that cannot be fully trusted. Instead, we argue that trustful predictions can be built by algorithms, while they run. We investigate this idea in the illustrative context of static scheduling with exponential job sizes. Indeed, we prove that algorithms agnostic to this structure do not perform better than in the worst case. In contrast, when the expected job sizes are known, we show that the best algorithm using this information, called Follow-The-Perfect-Prediction (FTPP), exhibits much better performances. Then, we introduce two adaptive explore-then-commit types of algorithms: they both first (partially) learn expected job sizes and then follow FTPP once their self-predictions are confident enough. On the one hand, ETCU explores in "series", by completing jobs sequentially to acquire information. On the other hand, ETCRR, inspired by the optimal worst-case algorithm Round-Robin (RR), explores efficiently in "parallel". We prove that both of them asymptotically reach the performances of FTPP, with a faster rate for ETCRR. Those findings are empirically evaluated on synthetic data.

Robust Estimation of Discrete Distributions under Local Differential Privacy

Although robust learning and local differential privacy are both widely studied fields of research, combining the two settings is an almost unexplored topic. We consider the problem of estimating a discrete distribution in total variation from $n$ contaminated data batches under a local differential privacy constraint. A fraction $1-\epsilon$ of the batches contain $k$ i.i.d. samples drawn from a discrete distribution $p$ over $d$ elements. To protect the users' privacy, each of the samples is privatized using an $\alpha$-locally differentially private mechanism. The remaining $\epsilon n $ batches are an adversarial contamination. The minimax rate of estimation under contamination alone, with no privacy, is known to be $\epsilon/\sqrt{k}+\sqrt{d/kn}$, up to a $\sqrt{\log(1/\epsilon)}$ factor. Under the privacy constraint alone, the minimax rate of estimation is $\sqrt{d^2/\alpha^2 kn}$. We show that combining the two constraints leads to a minimax estimation rate of $\epsilon\sqrt{d/\alpha^2 k}+\sqrt{d^2/\alpha^2 kn}$ up to a $\sqrt{\log(1/\epsilon)}$ factor, larger than the sum of the two separate rates. We provide a polynomial-time algorithm achieving this bound, as well as a matching information theoretic lower bound.

Pure Exploration and Regret Minimization in Matching Bandits

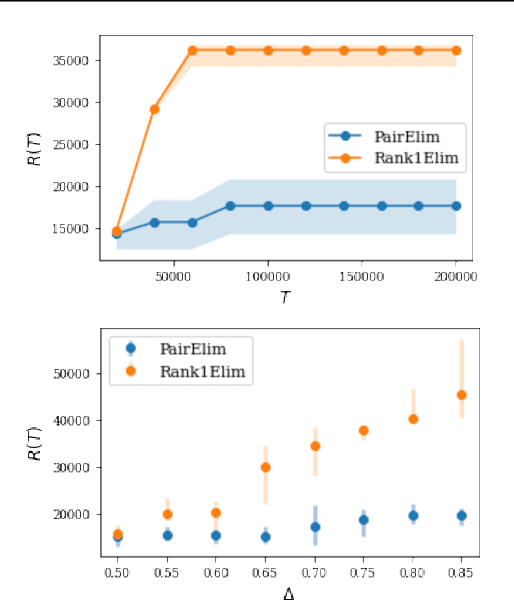
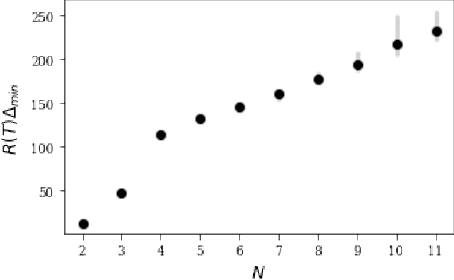
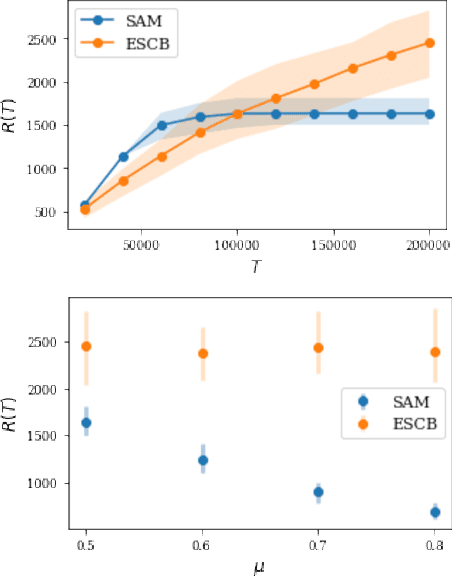
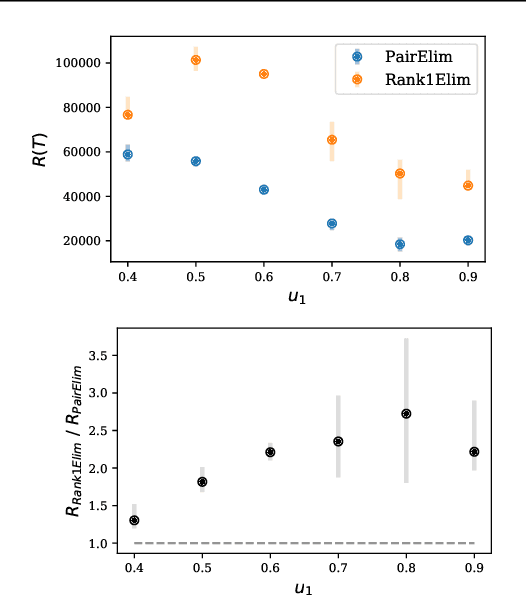
Finding an optimal matching in a weighted graph is a standard combinatorial problem. We consider its semi-bandit version where either a pair or a full matching is sampled sequentially. We prove that it is possible to leverage a rank-1 assumption on the adjacency matrix to reduce the sample complexity and the regret of off-the-shelf algorithms up to reaching a linear dependency in the number of vertices (up to poly log terms).

Online Matching in Sparse Random Graphs: Non-Asymptotic Performances of Greedy Algorithm

Motivated by sequential budgeted allocation problems, we investigate online matching problems where connections between vertices are not i.i.d., but they have fixed degree distributions -- the so-called configuration model. We estimate the competitive ratio of the simplest algorithm, GREEDY, by approximating some relevant stochastic discrete processes by their continuous counterparts, that are solutions of an explicit system of partial differential equations. This technique gives precise bounds on the estimation errors, with arbitrarily high probability as the problem size increases. In particular, it allows the formal comparison between different configuration models. We also prove that, quite surprisingly, GREEDY can have better performance guarantees than RANKING, another celebrated algorithm for online matching that usually outperforms the former.

Decentralized Learning in Online Queuing Systems

Motivated by packet routing in computer networks, online queuing systems are composed of queues receiving packets at different rates. Repeatedly, they send packets to servers, each of them treating only at most one packet at a time. In the centralized case, the number of accumulated packets remains bounded (i.e., the system is \textit{stable}) as long as the ratio between service rates and arrival rates is larger than $1$. In the decentralized case, individual no-regret strategies ensures stability when this ratio is larger than $2$. Yet, myopically minimizing regret disregards the long term effects due to the carryover of packets to further rounds. On the other hand, minimizing long term costs leads to stable Nash equilibria as soon as the ratio exceeds $\frac{e}{e-1}$. Stability with decentralized learning strategies with a ratio below $2$ was a major remaining question. We first argue that for ratios up to $2$, cooperation is required for stability of learning strategies, as selfish minimization of policy regret, a \textit{patient} notion of regret, might indeed still be unstable in this case. We therefore consider cooperative queues and propose the first learning decentralized algorithm guaranteeing stability of the system as long as the ratio of rates is larger than $1$, thus reaching performances comparable to centralized strategies.