Pure Exploration and Regret Minimization in Matching Bandits
Paper and Code
Jul 31, 2021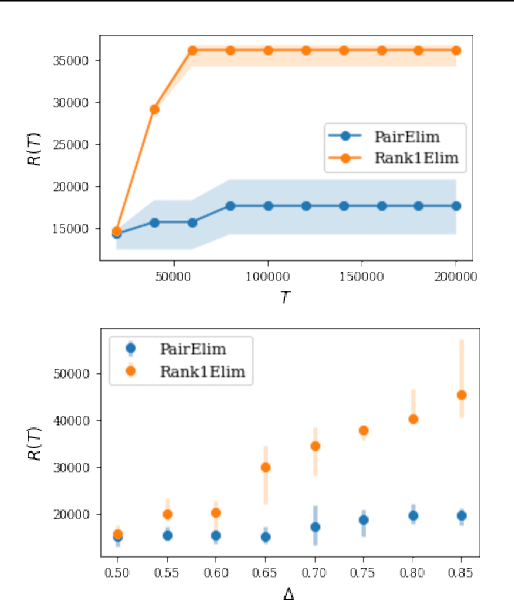
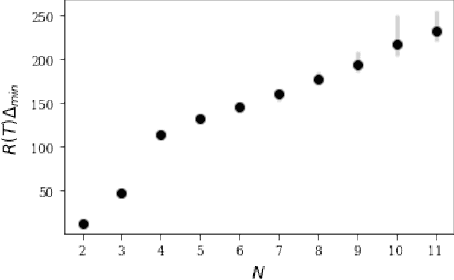
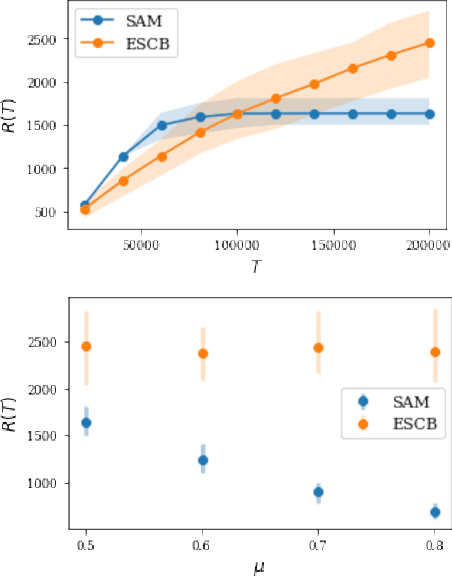
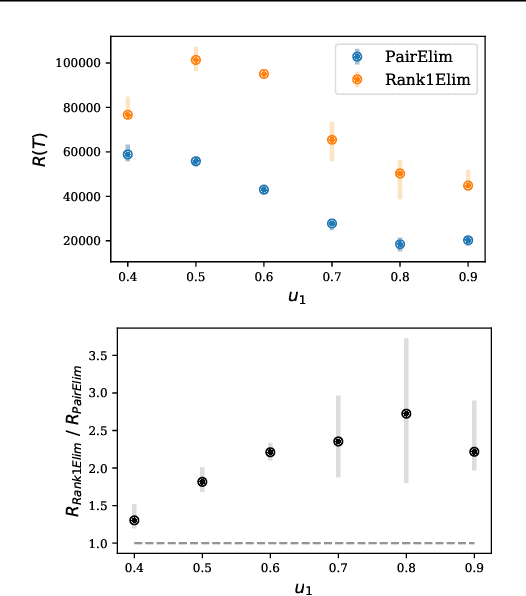
Finding an optimal matching in a weighted graph is a standard combinatorial problem. We consider its semi-bandit version where either a pair or a full matching is sampled sequentially. We prove that it is possible to leverage a rank-1 assumption on the adjacency matrix to reduce the sample complexity and the regret of off-the-shelf algorithms up to reaching a linear dependency in the number of vertices (up to poly log terms).
* Proceedings of the 38th International Conference on Machine
Learning, PMLR 139, 2021
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge