Pareto-Optimal Fairness-Utility Amortizations in Rankings with a DBN Exposure Model

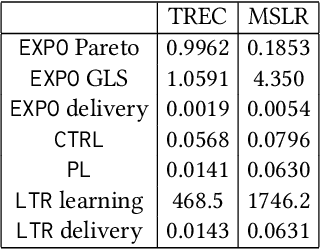
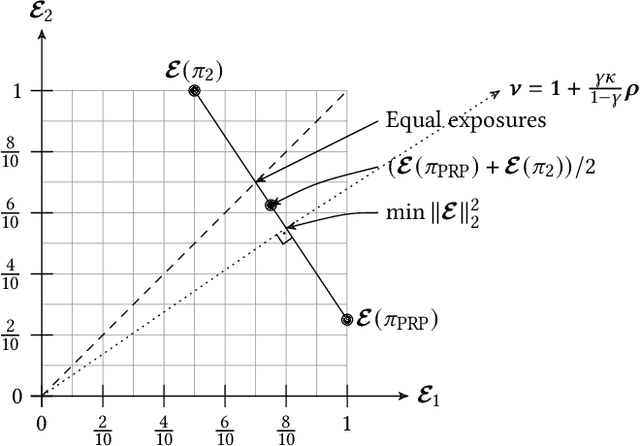
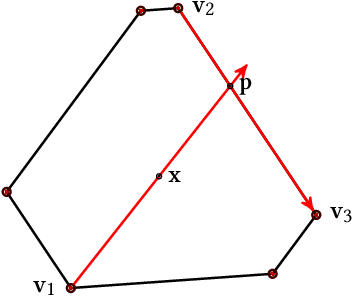
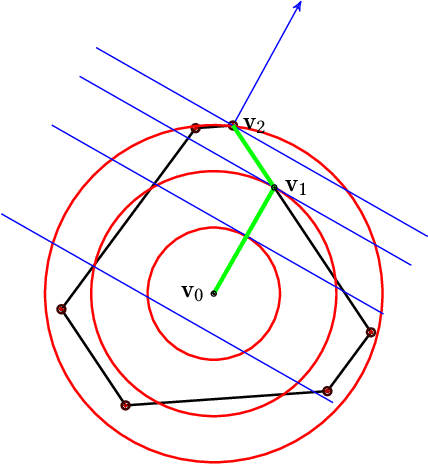
In recent years, it has become clear that rankings delivered in many areas need not only be useful to the users but also respect fairness of exposure for the item producers. We consider the problem of finding ranking policies that achieve a Pareto-optimal tradeoff between these two aspects. Several methods were proposed to solve it; for instance a popular one is to use linear programming with a Birkhoff-von Neumann decomposition. These methods, however, are based on a classical Position Based exposure Model (PBM), which assumes independence between the items (hence the exposure only depends on the rank). In many applications, this assumption is unrealistic and the community increasingly moves towards considering other models that include dependences, such as the Dynamic Bayesian Network (DBN) exposure model. For such models, computing (exact) optimal fair ranking policies remains an open question. We answer this question by leveraging a new geometrical method based on the so-called expohedron proposed recently for the PBM (Kletti et al., WSDM'22). We lay out the structure of a new geometrical object (the DBN-expohedron), and propose for it a Carath\'eodory decomposition algorithm of complexity $O(n^3)$, where $n$ is the number of documents to rank. Such an algorithm enables expressing any feasible expected exposure vector as a distribution over at most $n$ rankings; furthermore we show that we can compute the whole set of Pareto-optimal expected exposure vectors with the same complexity $O(n^3)$. Our work constitutes the first exact algorithm able to efficiently find a Pareto-optimal distribution of rankings. It is applicable to a broad range of fairness notions, including classical notions of meritocratic and demographic fairness. We empirically evaluate our method on the TREC2020 and MSLR datasets and compare it to several baselines in terms of Pareto-optimality and speed.