Benjamin Roussillon
Scalable Optimal Classifiers for Adversarial Settings under Uncertainty
Jun 28, 2021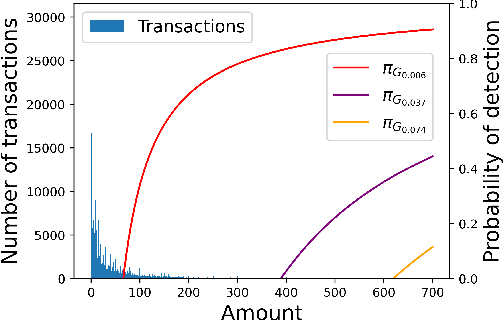
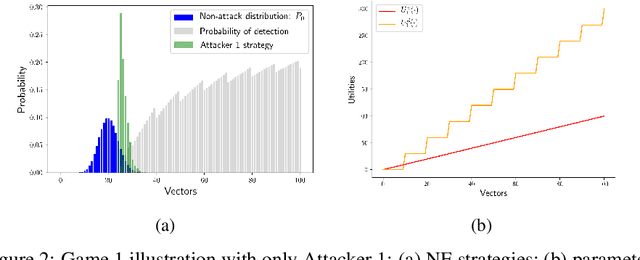
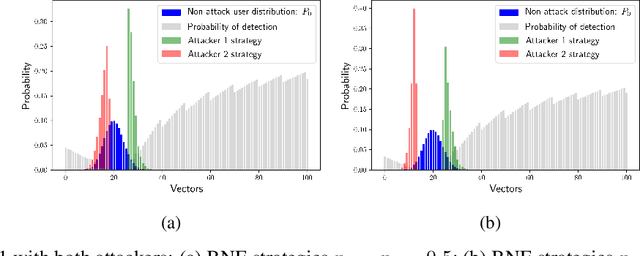
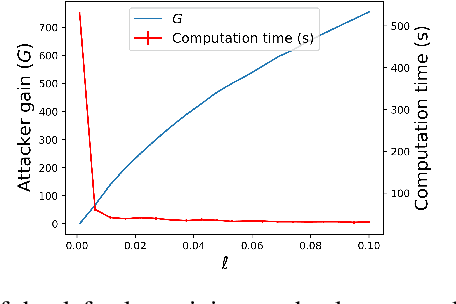
Abstract:We consider the problem of finding optimal classifiers in an adversarial setting where the class-1 data is generated by an attacker whose objective is not known to the defender -- an aspect that is key to realistic applications but has so far been overlooked in the literature. To model this situation, we propose a Bayesian game framework where the defender chooses a classifier with no a priori restriction on the set of possible classifiers. The key difficulty in the proposed framework is that the set of possible classifiers is exponential in the set of possible data, which is itself exponential in the number of features used for classification. To counter this, we first show that Bayesian Nash equilibria can be characterized completely via functional threshold classifiers with a small number of parameters. We then show that this low-dimensional characterization enables to develop a training method to compute provably approximately optimal classifiers in a scalable manner; and to develop a learning algorithm for the online setting with low regret (both independent of the dimension of the set of possible data). We illustrate our results through simulations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge