Correction to "Wasserstein distance estimates for the distributions of numerical approximations to ergodic stochastic differential equations"

A method for analyzing non-asymptotic guarantees of numerical discretizations of ergodic SDEs in Wasserstein-2 distance is presented by Sanz-Serna and Zygalakis in ``Wasserstein distance estimates for the distributions of numerical approximations to ergodic stochastic differential equations". They analyze the UBU integrator which is strong order two and only requires one gradient evaluation per step, resulting in desirable non-asymptotic guarantees, in particular $\mathcal{O}(d^{1/4}\epsilon^{-1/2})$ steps to reach a distance of $\epsilon > 0$ in Wasserstein-2 distance away from the target distribution. However, there is a mistake in the local error estimates in Sanz-Serna and Zygalakis (2021), in particular, a stronger assumption is needed to achieve these complexity estimates. This note reconciles the theory with the dimension dependence observed in practice in many applications of interest.

Unbiased Kinetic Langevin Monte Carlo with Inexact Gradients

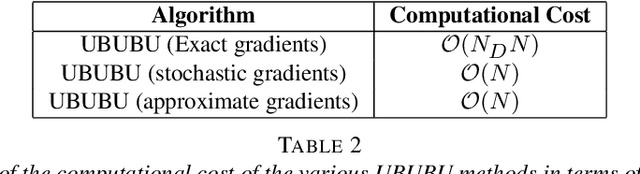
We present an unbiased method for Bayesian posterior means based on kinetic Langevin dynamics that combines advanced splitting methods with enhanced gradient approximations. Our approach avoids Metropolis correction by coupling Markov chains at different discretization levels in a multilevel Monte Carlo approach. Theoretical analysis demonstrates that our proposed estimator is unbiased, attains finite variance, and satisfies a central limit theorem. It can achieve accuracy $\epsilon>0$ for estimating expectations of Lipschitz functions in $d$ dimensions with $\mathcal{O}(d^{1/4}\epsilon^{-2})$ expected gradient evaluations, without assuming warm start. We exhibit similar bounds using both approximate and stochastic gradients, and our method's computational cost is shown to scale logarithmically with the size of the dataset. The proposed method is tested using a multinomial regression problem on the MNIST dataset and a Poisson regression model for soccer scores. Experiments indicate that the number of gradient evaluations per effective sample is independent of dimension, even when using inexact gradients. For product distributions, we give dimension-independent variance bounds. Our results demonstrate that the unbiased algorithm we present can be much more efficient than the ``gold-standard" randomized Hamiltonian Monte Carlo.

On Mixing Times of Metropolized Algorithm With Optimization Step (MAO) : A New Framework

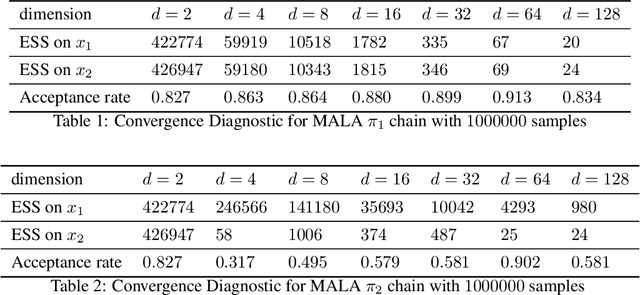
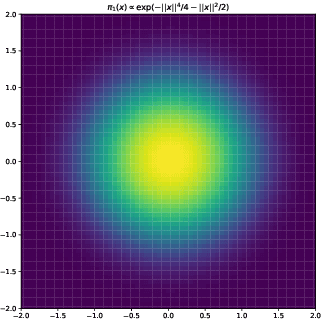
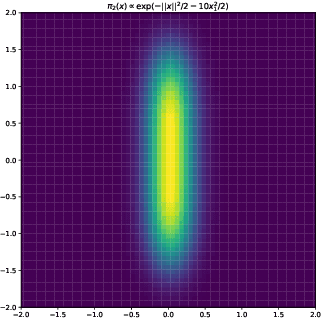
In this paper, we consider sampling from a class of distributions with thin tails supported on $\mathbb{R}^d$ and make two primary contributions. First, we propose a new Metropolized Algorithm With Optimization Step (MAO), which is well suited for such targets. Our algorithm is capable of sampling from distributions where the Metropolis-adjusted Langevin algorithm (MALA) is not converging or lacking in theoretical guarantees. Second, we derive upper bounds on the mixing time of MAO. Our results are supported by simulations on multiple target distributions.

Efficient MCMC Sampling with Dimension-Free Convergence Rate using ADMM-type Splitting

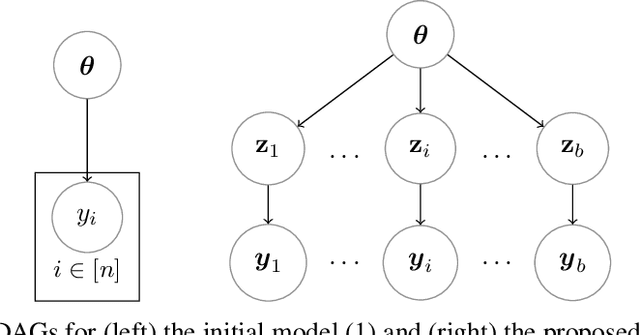
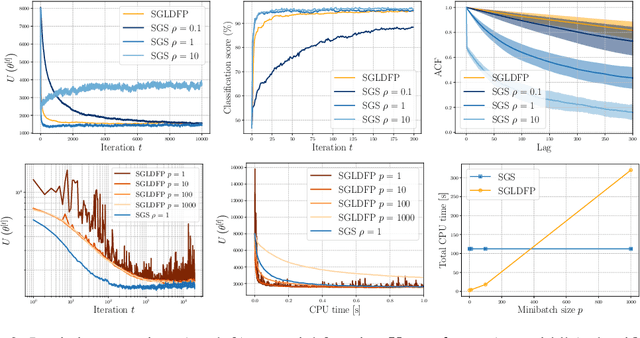
Performing exact Bayesian inference for complex models is intractable. Markov chain Monte Carlo (MCMC) algorithms can provide reliable approximations of the posterior distribution but are computationally expensive for large datasets. A standard approach to mitigate this complexity consists of using subsampling techniques or distributing the data across a cluster. However, these approaches are typically unreliable in high-dimensional scenarios. We focus here on an alternative class of MCMC schemes exploiting a splitting strategy akin to the one used by the celebrated ADMM optimization algorithm. These methods, proposed recently in [43, 51], appear to provide empirically state-of-the-art performance. We generalize here these ideas and propose a detailed theoretical study of one of these algorithms known as the Split Gibbs Sampler. Under regularity conditions, we establish explicit dimension-free convergence rates for this scheme using Ricci curvature and coupling ideas. We demonstrate experimentally the excellent performance of these MCMC schemes on various applications.

Hamiltonian Descent Methods

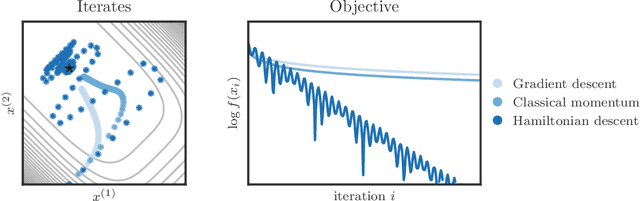
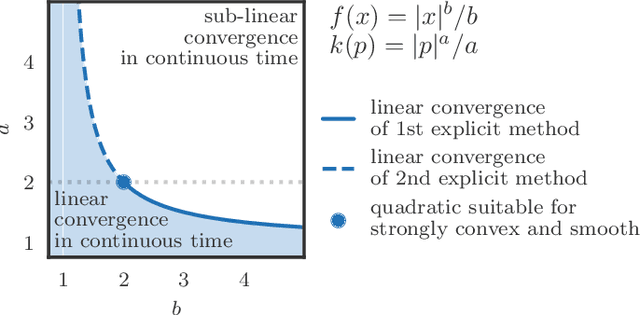
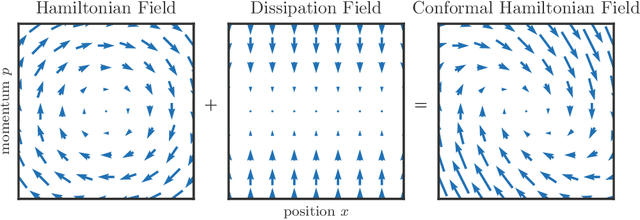
We propose a family of optimization methods that achieve linear convergence using first-order gradient information and constant step sizes on a class of convex functions much larger than the smooth and strongly convex ones. This larger class includes functions whose second derivatives may be singular or unbounded at their minima. Our methods are discretizations of conformal Hamiltonian dynamics, which generalize the classical momentum method to model the motion of a particle with non-standard kinetic energy exposed to a dissipative force and the gradient field of the function of interest. They are first-order in the sense that they require only gradient computation. Yet, crucially the kinetic gradient map can be designed to incorporate information about the convex conjugate in a fashion that allows for linear convergence on convex functions that may be non-smooth or non-strongly convex. We study in detail one implicit and two explicit methods. For one explicit method, we provide conditions under which it converges to stationary points of non-convex functions. For all, we provide conditions on the convex function and kinetic energy pair that guarantee linear convergence, and show that these conditions can be satisfied by functions with power growth. In sum, these methods expand the class of convex functions on which linear convergence is possible with first-order computation.