Variational Approximations for Robust Bayesian Inference via Rho-Posteriors

The $ρ$-posterior framework provides universal Bayesian estimation with explicit contamination rates and optimal convergence guarantees, but has remained computationally difficult due to an optimization over reference distributions that precludes intractable posterior computation. We develop a PAC-Bayesian framework that recovers these theoretical guarantees through temperature-dependent Gibbs posteriors, deriving finite-sample oracle inequalities with explicit rates and introducing tractable variational approximations that inherit the robustness properties of exact $ρ$-posteriors. Numerical experiments demonstrate that this approach achieves theoretical contamination rates while remaining computationally feasible, providing the first practical implementation of $ρ$-posterior inference with rigorous finite-sample guarantees.

On Mixing Times of Metropolized Algorithm With Optimization Step (MAO) : A New Framework

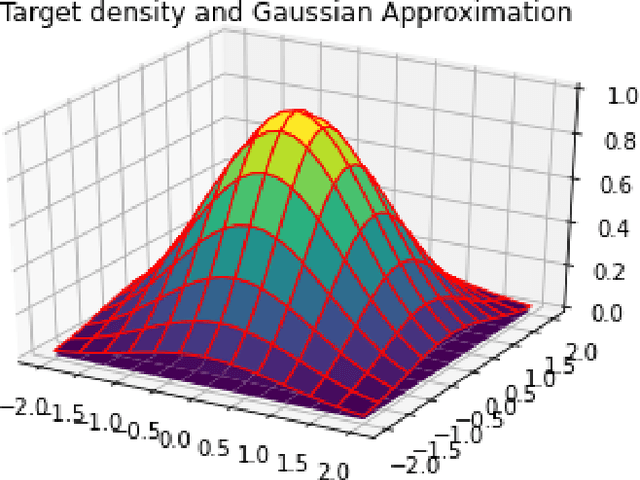
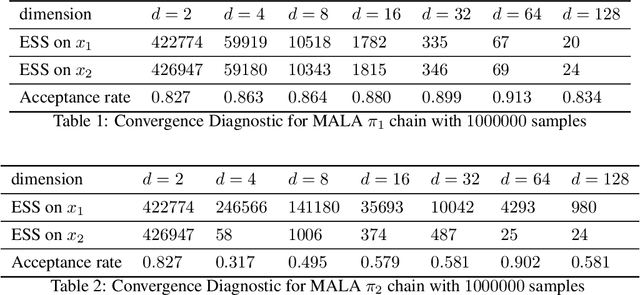
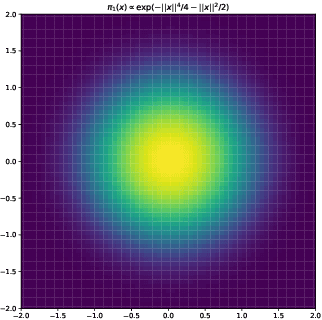
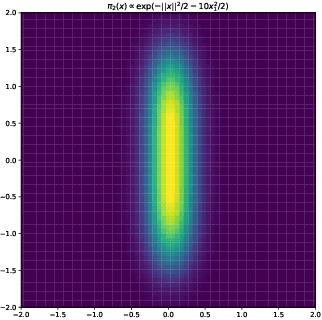
In this paper, we consider sampling from a class of distributions with thin tails supported on $\mathbb{R}^d$ and make two primary contributions. First, we propose a new Metropolized Algorithm With Optimization Step (MAO), which is well suited for such targets. Our algorithm is capable of sampling from distributions where the Metropolis-adjusted Langevin algorithm (MALA) is not converging or lacking in theoretical guarantees. Second, we derive upper bounds on the mixing time of MAO. Our results are supported by simulations on multiple target distributions.