Efficient MCMC Sampling with Dimension-Free Convergence Rate using ADMM-type Splitting

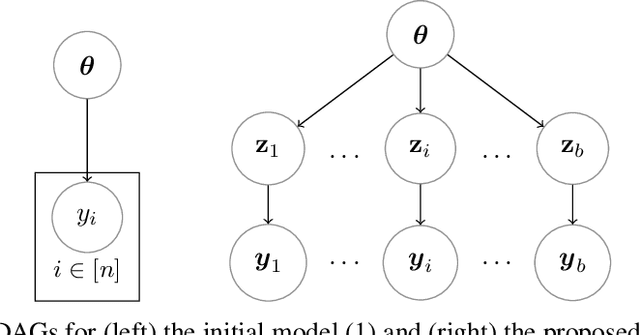
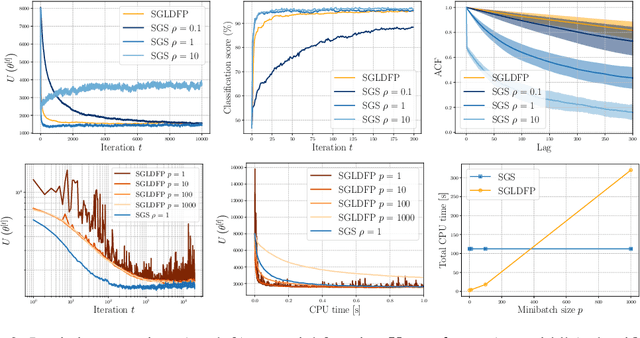
Performing exact Bayesian inference for complex models is intractable. Markov chain Monte Carlo (MCMC) algorithms can provide reliable approximations of the posterior distribution but are computationally expensive for large datasets. A standard approach to mitigate this complexity consists of using subsampling techniques or distributing the data across a cluster. However, these approaches are typically unreliable in high-dimensional scenarios. We focus here on an alternative class of MCMC schemes exploiting a splitting strategy akin to the one used by the celebrated ADMM optimization algorithm. These methods, proposed recently in [43, 51], appear to provide empirically state-of-the-art performance. We generalize here these ideas and propose a detailed theoretical study of one of these algorithms known as the Split Gibbs Sampler. Under regularity conditions, we establish explicit dimension-free convergence rates for this scheme using Ricci curvature and coupling ideas. We demonstrate experimentally the excellent performance of these MCMC schemes on various applications.