Randomised Splitting Methods and Stochastic Gradient Descent

We explore an explicit link between stochastic gradient descent using common batching strategies and splitting methods for ordinary differential equations. From this perspective, we introduce a new minibatching strategy (called Symmetric Minibatching Strategy) for stochastic gradient optimisation which shows greatly reduced stochastic gradient bias (from $\mathcal{O}(h^2)$ to $\mathcal{O}(h^4)$ in the optimiser stepsize $h$), when combined with momentum-based optimisers. We justify why momentum is needed to obtain the improved performance using the theory of backward analysis for splitting integrators and provide a detailed analytic computation of the stochastic gradient bias on a simple example. Further, we provide improved convergence guarantees for this new minibatching strategy using Lyapunov techniques that show reduced stochastic gradient bias for a fixed stepsize (or learning rate) over the class of strongly-convex and smooth objective functions. Via the same techniques we also improve the known results for the Random Reshuffling strategy for stochastic gradient descent methods with momentum. We argue that this also leads to a faster convergence rate when considering a decreasing stepsize schedule. Both the reduced bias and efficacy of decreasing stepsizes are demonstrated numerically on several motivating examples.

Random Reshuffling for Stochastic Gradient Langevin Dynamics

We examine the use of different randomisation policies for stochastic gradient algorithms used in sampling, based on first-order (or overdamped) Langevin dynamics, the most popular of which is known as Stochastic Gradient Langevin Dynamics. Conventionally, this algorithm is combined with a specific stochastic gradient strategy, called Robbins-Monro. In this work, we study an alternative strategy, Random Reshuffling, and show convincingly that it leads to improved performance via: a) a proof of reduced bias in the Wasserstein metric for strongly convex, gradient Lipschitz potentials; b) an analytical demonstration of reduced bias for a Gaussian model problem; and c) an empirical demonstration of reduced bias in numerical experiments for some logistic regression problems. This is especially important since Random Reshuffling is typically more efficient due to memory access and cache reasons. Such acceleration for the Random Reshuffling policy is familiar from the optimisation literature on stochastic gradient descent.

Correction to "Wasserstein distance estimates for the distributions of numerical approximations to ergodic stochastic differential equations"

A method for analyzing non-asymptotic guarantees of numerical discretizations of ergodic SDEs in Wasserstein-2 distance is presented by Sanz-Serna and Zygalakis in ``Wasserstein distance estimates for the distributions of numerical approximations to ergodic stochastic differential equations". They analyze the UBU integrator which is strong order two and only requires one gradient evaluation per step, resulting in desirable non-asymptotic guarantees, in particular $\mathcal{O}(d^{1/4}\epsilon^{-1/2})$ steps to reach a distance of $\epsilon > 0$ in Wasserstein-2 distance away from the target distribution. However, there is a mistake in the local error estimates in Sanz-Serna and Zygalakis (2021), in particular, a stronger assumption is needed to achieve these complexity estimates. This note reconciles the theory with the dimension dependence observed in practice in many applications of interest.

Unbiased Kinetic Langevin Monte Carlo with Inexact Gradients

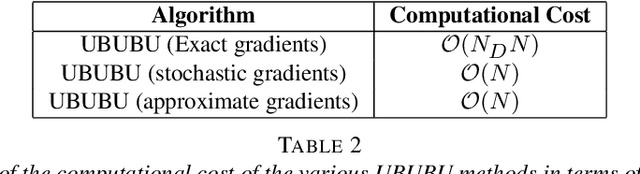
We present an unbiased method for Bayesian posterior means based on kinetic Langevin dynamics that combines advanced splitting methods with enhanced gradient approximations. Our approach avoids Metropolis correction by coupling Markov chains at different discretization levels in a multilevel Monte Carlo approach. Theoretical analysis demonstrates that our proposed estimator is unbiased, attains finite variance, and satisfies a central limit theorem. It can achieve accuracy $\epsilon>0$ for estimating expectations of Lipschitz functions in $d$ dimensions with $\mathcal{O}(d^{1/4}\epsilon^{-2})$ expected gradient evaluations, without assuming warm start. We exhibit similar bounds using both approximate and stochastic gradients, and our method's computational cost is shown to scale logarithmically with the size of the dataset. The proposed method is tested using a multinomial regression problem on the MNIST dataset and a Poisson regression model for soccer scores. Experiments indicate that the number of gradient evaluations per effective sample is independent of dimension, even when using inexact gradients. For product distributions, we give dimension-independent variance bounds. Our results demonstrate that the unbiased algorithm we present can be much more efficient than the ``gold-standard" randomized Hamiltonian Monte Carlo.