Nikita Kotelevskii
Uncertainty Quantification for Regression using Proper Scoring Rules
Sep 30, 2025
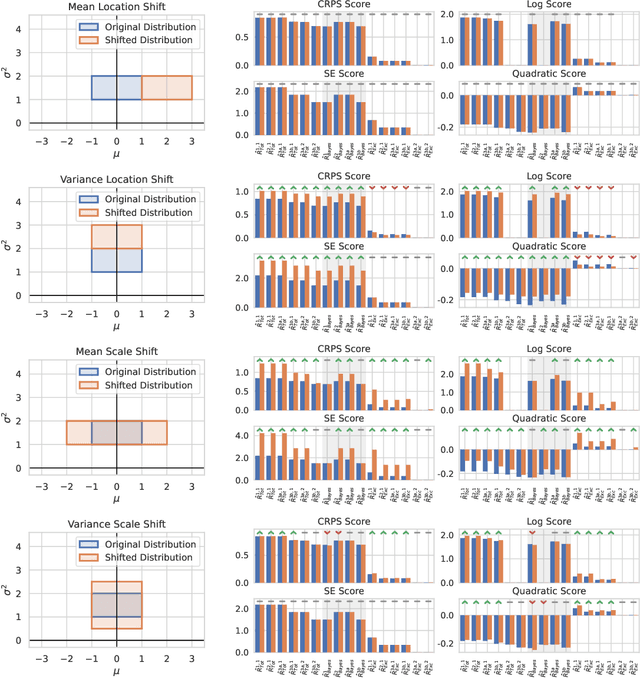


Abstract:Quantifying uncertainty of machine learning model predictions is essential for reliable decision-making, especially in safety-critical applications. Recently, uncertainty quantification (UQ) theory has advanced significantly, building on a firm basis of learning with proper scoring rules. However, these advances were focused on classification, while extending these ideas to regression remains challenging. In this work, we introduce a unified UQ framework for regression based on proper scoring rules, such as CRPS, logarithmic, squared error, and quadratic scores. We derive closed-form expressions for the resulting uncertainty measures under practical parametric assumptions and show how to estimate them using ensembles of models. In particular, the derived uncertainty measures naturally decompose into aleatoric and epistemic components. The framework recovers popular regression UQ measures based on predictive variance and differential entropy. Our broad evaluation on synthetic and real-world regression datasets provides guidance for selecting reliable UQ measures.
Who to Trust? Aggregating Client Knowledge in Logit-Based Federated Learning
Sep 18, 2025Abstract:Federated learning (FL) usually shares model weights or gradients, which is costly for large models. Logit-based FL reduces this cost by sharing only logits computed on a public proxy dataset. However, aggregating information from heterogeneous clients is still challenging. This paper studies this problem, introduces and compares three logit aggregation methods: simple averaging, uncertainty-weighted averaging, and a learned meta-aggregator. Evaluated on MNIST and CIFAR-10, these methods reduce communication overhead, improve robustness under non-IID data, and achieve accuracy competitive with centralized training.
Adaptive Temperature Scaling with Conformal Prediction
May 21, 2025Abstract:Conformal prediction enables the construction of high-coverage prediction sets for any pre-trained model, guaranteeing that the true label lies within the set with a specified probability. However, these sets do not provide probability estimates for individual labels, limiting their practical use. In this paper, we propose, to the best of our knowledge, the first method for assigning calibrated probabilities to elements of a conformal prediction set. Our approach frames this as an adaptive calibration problem, selecting an input-specific temperature parameter to match the desired coverage level. Experiments on several challenging image classification datasets demonstrate that our method maintains coverage guarantees while significantly reducing expected calibration error.
Predictive Uncertainty Quantification via Risk Decompositions for Strictly Proper Scoring Rules
Feb 16, 2024



Abstract:Distinguishing sources of predictive uncertainty is of crucial importance in the application of forecasting models across various domains. Despite the presence of a great variety of proposed uncertainty measures, there are no strict definitions to disentangle them. Furthermore, the relationship between different measures of uncertainty quantification remains somewhat unclear. In this work, we introduce a general framework, rooted in statistical reasoning, which not only allows the creation of new uncertainty measures but also clarifies their interrelations. Our approach leverages statistical risk to distinguish aleatoric and epistemic uncertainty components and utilizes proper scoring rules to quantify them. To make it practically tractable, we propose an idea to incorporate Bayesian reasoning into this framework and discuss the properties of the proposed approximation.
Efficient Conformal Prediction under Data Heterogeneity
Dec 25, 2023



Abstract:Conformal Prediction (CP) stands out as a robust framework for uncertainty quantification, which is crucial for ensuring the reliability of predictions. However, common CP methods heavily rely on data exchangeability, a condition often violated in practice. Existing approaches for tackling non-exchangeability lead to methods that are not computable beyond the simplest examples. This work introduces a new efficient approach to CP that produces provably valid confidence sets for fairly general non-exchangeable data distributions. We illustrate the general theory with applications to the challenging setting of federated learning under data heterogeneity between agents. Our method allows constructing provably valid personalized prediction sets for agents in a fully federated way. The effectiveness of the proposed method is demonstrated in a series of experiments on real-world datasets.
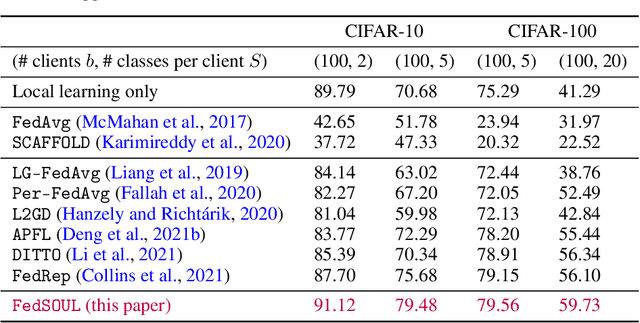
Dirichlet-based Uncertainty Quantification for Personalized Federated Learning with Improved Posterior Networks
Dec 18, 2023



Abstract:In modern federated learning, one of the main challenges is to account for inherent heterogeneity and the diverse nature of data distributions for different clients. This problem is often addressed by introducing personalization of the models towards the data distribution of the particular client. However, a personalized model might be unreliable when applied to the data that is not typical for this client. Eventually, it may perform worse for these data than the non-personalized global model trained in a federated way on the data from all the clients. This paper presents a new approach to federated learning that allows selecting a model from global and personalized ones that would perform better for a particular input point. It is achieved through a careful modeling of predictive uncertainties that helps to detect local and global in- and out-of-distribution data and use this information to select the model that is confident in a prediction. The comprehensive experimental evaluation on the popular real-world image datasets shows the superior performance of the model in the presence of out-of-distribution data while performing on par with state-of-the-art personalized federated learning algorithms in the standard scenarios.
FedPop: A Bayesian Approach for Personalised Federated Learning
Jun 07, 2022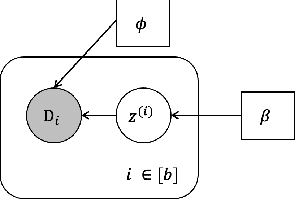
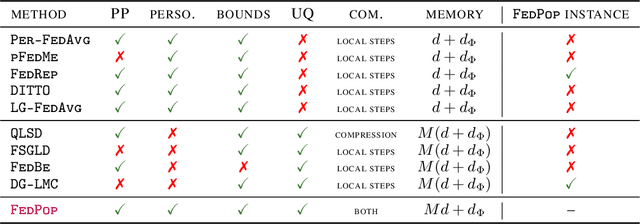
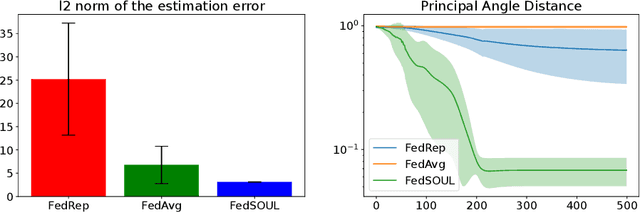
Abstract:Personalised federated learning (FL) aims at collaboratively learning a machine learning model taylored for each client. Albeit promising advances have been made in this direction, most of existing approaches works do not allow for uncertainty quantification which is crucial in many applications. In addition, personalisation in the cross-device setting still involves important issues, especially for new clients or those having small number of observations. This paper aims at filling these gaps. To this end, we propose a novel methodology coined FedPop by recasting personalised FL into the population modeling paradigm where clients' models involve fixed common population parameters and random effects, aiming at explaining data heterogeneity. To derive convergence guarantees for our scheme, we introduce a new class of federated stochastic optimisation algorithms which relies on Markov chain Monte Carlo methods. Compared to existing personalised FL methods, the proposed methodology has important benefits: it is robust to client drift, practical for inference on new clients, and above all, enables uncertainty quantification under mild computational and memory overheads. We provide non-asymptotic convergence guarantees for the proposed algorithms and illustrate their performances on various personalised federated learning tasks.
NUQ: Nonparametric Uncertainty Quantification for Deterministic Neural Networks
Feb 07, 2022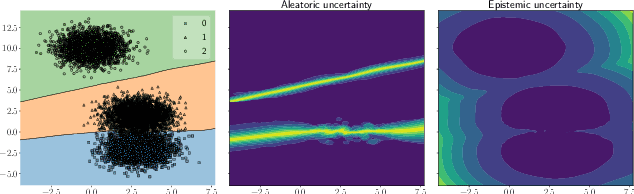

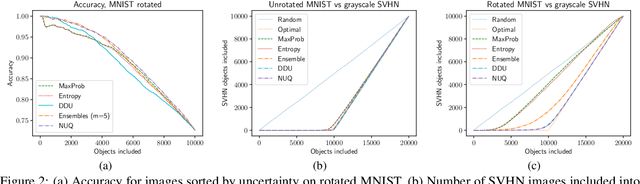

Abstract:This paper proposes a fast and scalable method for uncertainty quantification of machine learning models' predictions. First, we show the principled way to measure the uncertainty of predictions for a classifier based on Nadaraya-Watson's nonparametric estimate of the conditional label distribution. Importantly, the approach allows to disentangle explicitly aleatoric and epistemic uncertainties. The resulting method works directly in the feature space. However, one can apply it to any neural network by considering an embedding of the data induced by the network. We demonstrate the strong performance of the method in uncertainty estimation tasks on a variety of real-world image datasets, such as MNIST, SVHN, CIFAR-100 and several versions of ImageNet.
Monte Carlo Variational Auto-Encoders
Jun 30, 2021



Abstract:Variational auto-encoders (VAE) are popular deep latent variable models which are trained by maximizing an Evidence Lower Bound (ELBO). To obtain tighter ELBO and hence better variational approximations, it has been proposed to use importance sampling to get a lower variance estimate of the evidence. However, importance sampling is known to perform poorly in high dimensions. While it has been suggested many times in the literature to use more sophisticated algorithms such as Annealed Importance Sampling (AIS) and its Sequential Importance Sampling (SIS) extensions, the potential benefits brought by these advanced techniques have never been realized for VAE: the AIS estimate cannot be easily differentiated, while SIS requires the specification of carefully chosen backward Markov kernels. In this paper, we address both issues and demonstrate the performance of the resulting Monte Carlo VAEs on a variety of applications.
MetFlow: A New Efficient Method for Bridging the Gap between Markov Chain Monte Carlo and Variational Inference
Feb 27, 2020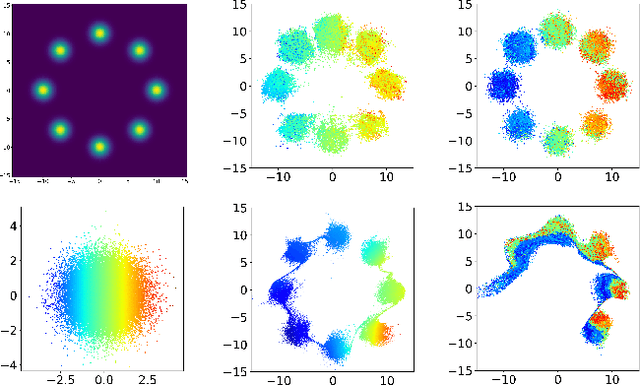
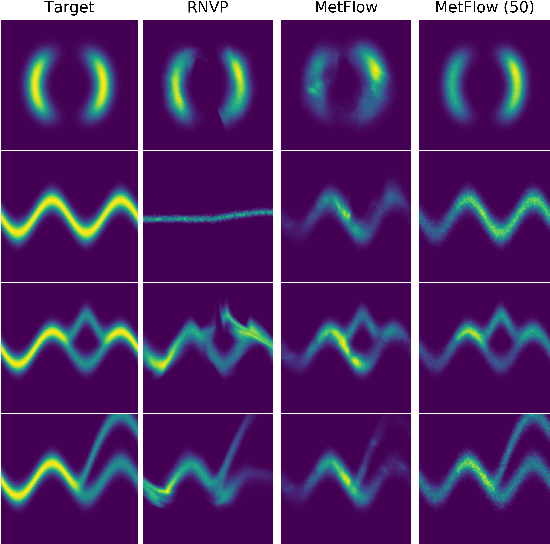


Abstract:In this contribution, we propose a new computationally efficient method to combine Variational Inference (VI) with Markov Chain Monte Carlo (MCMC). This approach can be used with generic MCMC kernels, but is especially well suited to \textit{MetFlow}, a novel family of MCMC algorithms we introduce, in which proposals are obtained using Normalizing Flows. The marginal distribution produced by such MCMC algorithms is a mixture of flow-based distributions, thus drastically increasing the expressivity of the variational family. Unlike previous methods following this direction, our approach is amenable to the reparametrization trick and does not rely on computationally expensive reverse kernels. Extensive numerical experiments show clear computational and performance improvements over state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge