Conditionally valid Probabilistic Conformal Prediction

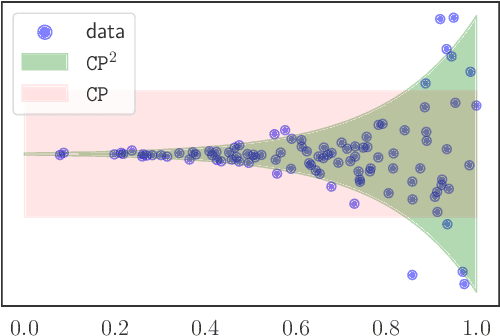
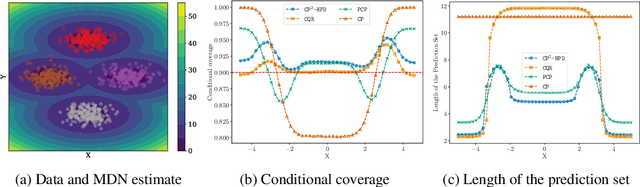
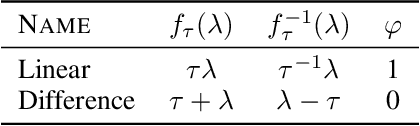
We develop a new method for creating prediction sets that combines the flexibility of conformal methods with an estimate of the conditional distribution $P_{Y \mid X}$. Most existing methods, such as conformalized quantile regression and probabilistic conformal prediction, only offer marginal coverage guarantees. Our approach extends these methods to achieve conditional coverage, which is essential for many practical applications. While exact conditional guarantees are impossible without assumptions on the data distribution, we provide non-asymptotic bounds that explicitly depend on the quality of the available estimate of the conditional distribution. Our confidence sets are highly adaptive to the local structure of the data, making them particularly useful in high heteroskedasticity situations. We demonstrate the effectiveness of our approach through extensive simulations, showing that it outperforms existing methods in terms of conditional coverage and improves the reliability of statistical inference in a wide range of applications.

Efficient Conformal Prediction under Data Heterogeneity

Conformal Prediction (CP) stands out as a robust framework for uncertainty quantification, which is crucial for ensuring the reliability of predictions. However, common CP methods heavily rely on data exchangeability, a condition often violated in practice. Existing approaches for tackling non-exchangeability lead to methods that are not computable beyond the simplest examples. This work introduces a new efficient approach to CP that produces provably valid confidence sets for fairly general non-exchangeable data distributions. We illustrate the general theory with applications to the challenging setting of federated learning under data heterogeneity between agents. Our method allows constructing provably valid personalized prediction sets for agents in a fully federated way. The effectiveness of the proposed method is demonstrated in a series of experiments on real-world datasets.

Selective Nonparametric Regression via Testing

Prediction with the possibility of abstention (or selective prediction) is an important problem for error-critical machine learning applications. While well-studied in the classification setup, selective approaches to regression are much less developed. In this work, we consider the nonparametric heteroskedastic regression problem and develop an abstention procedure via testing the hypothesis on the value of the conditional variance at a given point. Unlike existing methods, the proposed one allows to account not only for the value of the variance itself but also for the uncertainty of the corresponding variance predictor. We prove non-asymptotic bounds on the risk of the resulting estimator and show the existence of several different convergence regimes. Theoretical analysis is illustrated with a series of experiments on simulated and real-world data.

Scalable computation of prediction intervals for neural networks via matrix sketching

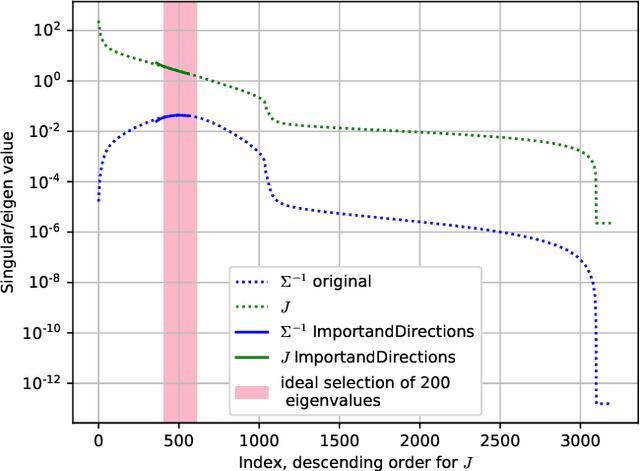
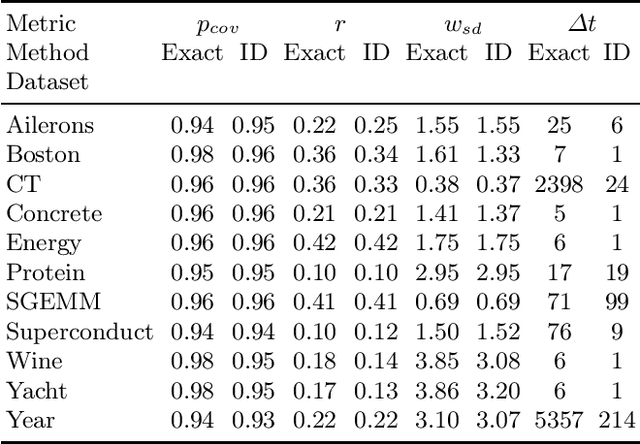
Accounting for the uncertainty in the predictions of modern neural networks is a challenging and important task in many domains. Existing algorithms for uncertainty estimation require modifying the model architecture and training procedure (e.g., Bayesian neural networks) or dramatically increase the computational cost of predictions such as approaches based on ensembling. This work proposes a new algorithm that can be applied to a given trained neural network and produces approximate prediction intervals. The method is based on the classical delta method in statistics but achieves computational efficiency by using matrix sketching to approximate the Jacobian matrix. The resulting algorithm is competitive with state-of-the-art approaches for constructing predictive intervals on various regression datasets from the UCI repository.

NUQ: Nonparametric Uncertainty Quantification for Deterministic Neural Networks

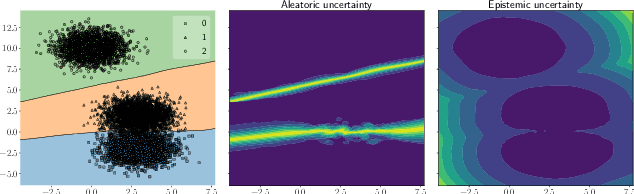
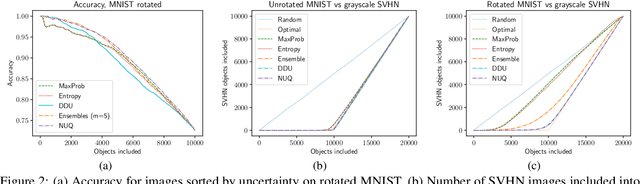
This paper proposes a fast and scalable method for uncertainty quantification of machine learning models' predictions. First, we show the principled way to measure the uncertainty of predictions for a classifier based on Nadaraya-Watson's nonparametric estimate of the conditional label distribution. Importantly, the approach allows to disentangle explicitly aleatoric and epistemic uncertainties. The resulting method works directly in the feature space. However, one can apply it to any neural network by considering an embedding of the data induced by the network. We demonstrate the strong performance of the method in uncertainty estimation tasks on a variety of real-world image datasets, such as MNIST, SVHN, CIFAR-100 and several versions of ImageNet.