Multivariate Latent Recalibration for Conditional Normalizing Flows

Reliably characterizing the full conditional distribution of a multivariate response variable given a set of covariates is crucial for trustworthy decision-making. However, misspecified or miscalibrated multivariate models may yield a poor approximation of the joint distribution of the response variables, leading to unreliable predictions and suboptimal decisions. Furthermore, standard recalibration methods are primarily limited to univariate settings, while conformal prediction techniques, despite generating multivariate prediction regions with coverage guarantees, do not provide a full probability density function. We address this gap by first introducing a novel notion of latent calibration, which assesses probabilistic calibration in the latent space of a conditional normalizing flow. Second, we propose latent recalibration (LR), a novel post-hoc model recalibration method that learns a transformation of the latent space with finite-sample bounds on latent calibration. Unlike existing methods, LR produces a recalibrated distribution with an explicit multivariate density function while remaining computationally efficient. Extensive experiments on both tabular and image datasets show that LR consistently improves latent calibration error and the negative log-likelihood of the recalibrated models.

Rectifying Conformity Scores for Better Conditional Coverage

We present a new method for generating confidence sets within the split conformal prediction framework. Our method performs a trainable transformation of any given conformity score to improve conditional coverage while ensuring exact marginal coverage. The transformation is based on an estimate of the conditional quantile of conformity scores. The resulting method is particularly beneficial for constructing adaptive confidence sets in multi-output problems where standard conformal quantile regression approaches have limited applicability. We develop a theoretical bound that captures the influence of the accuracy of the quantile estimate on the approximate conditional validity, unlike classical bounds for conformal prediction methods that only offer marginal coverage. We experimentally show that our method is highly adaptive to the local data structure and outperforms existing methods in terms of conditional coverage, improving the reliability of statistical inference in various applications.

Multi-Output Conformal Regression: A Unified Comparative Study with New Conformity Scores

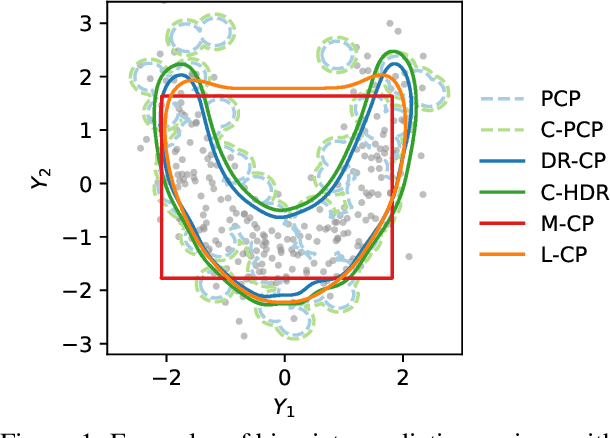
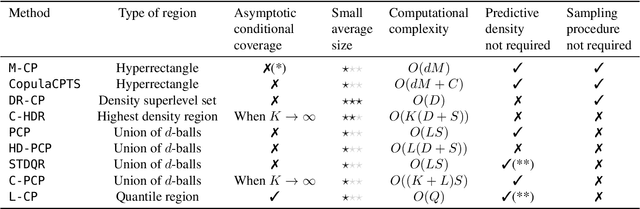
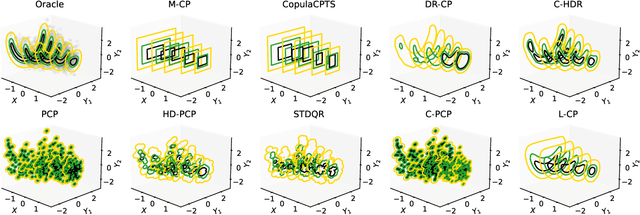
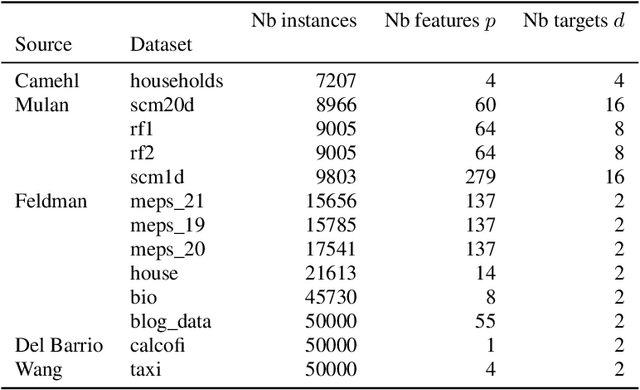
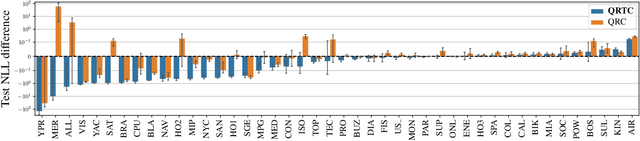
Quantifying uncertainty in multivariate regression is essential in many real-world applications, yet existing methods for constructing prediction regions often face limitations such as the inability to capture complex dependencies, lack of coverage guarantees, or high computational cost. Conformal prediction provides a robust framework for producing distribution-free prediction regions with finite-sample coverage guarantees. In this work, we present a unified comparative study of multi-output conformal methods, exploring their properties and interconnections. Based on our findings, we introduce two classes of conformity scores that achieve asymptotic conditional coverage: one is compatible with any generative model, and the other offers low computational cost by leveraging invertible generative models. Finally, we conduct a comprehensive empirical study across 32 tabular datasets to compare all the multi-output conformal methods considered in this work. All methods are implemented within a unified code base to ensure a fair and consistent comparison.

Probabilistic Calibration by Design for Neural Network Regression

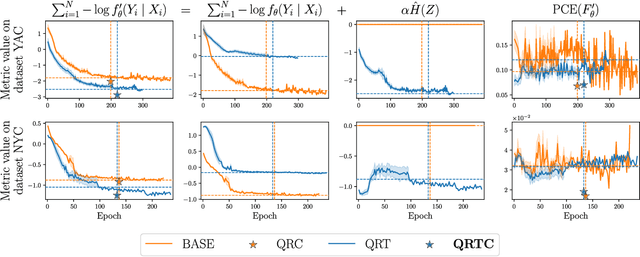
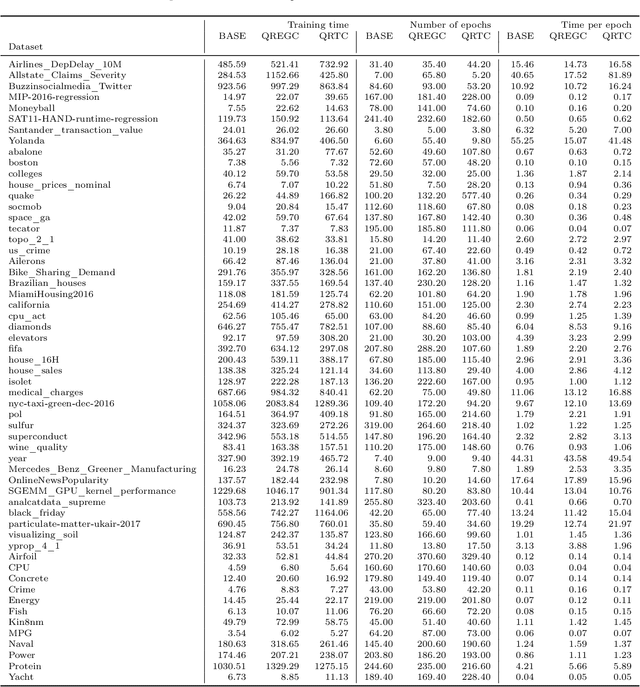
Generating calibrated and sharp neural network predictive distributions for regression problems is essential for optimal decision-making in many real-world applications. To address the miscalibration issue of neural networks, various methods have been proposed to improve calibration, including post-hoc methods that adjust predictions after training and regularization methods that act during training. While post-hoc methods have shown better improvement in calibration compared to regularization methods, the post-hoc step is completely independent of model training. We introduce a novel end-to-end model training procedure called Quantile Recalibration Training, integrating post-hoc calibration directly into the training process without additional parameters. We also present a unified algorithm that includes our method and other post-hoc and regularization methods, as particular cases. We demonstrate the performance of our method in a large-scale experiment involving 57 tabular regression datasets, showcasing improved predictive accuracy while maintaining calibration. We also conduct an ablation study to evaluate the significance of different components within our proposed method, as well as an in-depth analysis of the impact of the base model and different hyperparameters on predictive accuracy.

Distribution-Free Conformal Joint Prediction Regions for Neural Marked Temporal Point Processes

Sequences of labeled events observed at irregular intervals in continuous time are ubiquitous across various fields. Temporal Point Processes (TPPs) provide a mathematical framework for modeling these sequences, enabling inferences such as predicting the arrival time of future events and their associated label, called mark. However, due to model misspecification or lack of training data, these probabilistic models may provide a poor approximation of the true, unknown underlying process, with prediction regions extracted from them being unreliable estimates of the underlying uncertainty. This paper develops more reliable methods for uncertainty quantification in neural TPP models via the framework of conformal prediction. A primary objective is to generate a distribution-free joint prediction region for the arrival time and mark, with a finite-sample marginal coverage guarantee. A key challenge is to handle both a strictly positive, continuous response and a categorical response, without distributional assumptions. We first consider a simple but overly conservative approach that combines individual prediction regions for the event arrival time and mark. Then, we introduce a more effective method based on bivariate highest density regions derived from the joint predictive density of event arrival time and mark. By leveraging the dependencies between these two variables, this method exclude unlikely combinations of the two, resulting in sharper prediction regions while still attaining the pre-specified coverage level. We also explore the generation of individual univariate prediction regions for arrival times and marks through conformal regression and classification techniques. Moreover, we investigate the stronger notion of conditional coverage. Finally, through extensive experimentation on both simulated and real-world datasets, we assess the validity and efficiency of these methods.

A Large-Scale Study of Probabilistic Calibration in Neural Network Regression

Accurate probabilistic predictions are essential for optimal decision making. While neural network miscalibration has been studied primarily in classification, we investigate this in the less-explored domain of regression. We conduct the largest empirical study to date to assess the probabilistic calibration of neural networks. We also analyze the performance of recalibration, conformal, and regularization methods to enhance probabilistic calibration. Additionally, we introduce novel differentiable recalibration and regularization methods, uncovering new insights into their effectiveness. Our findings reveal that regularization methods offer a favorable tradeoff between calibration and sharpness. Post-hoc methods exhibit superior probabilistic calibration, which we attribute to the finite-sample coverage guarantee of conformal prediction. Furthermore, we demonstrate that quantile recalibration can be considered as a specific case of conformal prediction. Our study is fully reproducible and implemented in a common code base for fair comparisons.