Rectifying Conformity Scores for Better Conditional Coverage

We present a new method for generating confidence sets within the split conformal prediction framework. Our method performs a trainable transformation of any given conformity score to improve conditional coverage while ensuring exact marginal coverage. The transformation is based on an estimate of the conditional quantile of conformity scores. The resulting method is particularly beneficial for constructing adaptive confidence sets in multi-output problems where standard conformal quantile regression approaches have limited applicability. We develop a theoretical bound that captures the influence of the accuracy of the quantile estimate on the approximate conditional validity, unlike classical bounds for conformal prediction methods that only offer marginal coverage. We experimentally show that our method is highly adaptive to the local data structure and outperforms existing methods in terms of conditional coverage, improving the reliability of statistical inference in various applications.

Conditionally valid Probabilistic Conformal Prediction

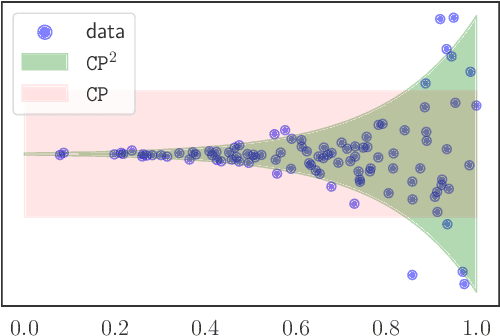
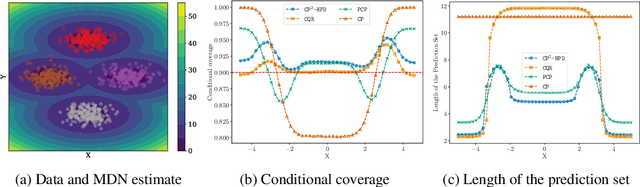
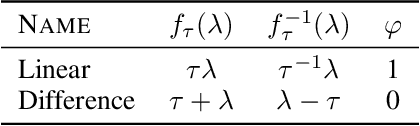
We develop a new method for creating prediction sets that combines the flexibility of conformal methods with an estimate of the conditional distribution $P_{Y \mid X}$. Most existing methods, such as conformalized quantile regression and probabilistic conformal prediction, only offer marginal coverage guarantees. Our approach extends these methods to achieve conditional coverage, which is essential for many practical applications. While exact conditional guarantees are impossible without assumptions on the data distribution, we provide non-asymptotic bounds that explicitly depend on the quality of the available estimate of the conditional distribution. Our confidence sets are highly adaptive to the local structure of the data, making them particularly useful in high heteroskedasticity situations. We demonstrate the effectiveness of our approach through extensive simulations, showing that it outperforms existing methods in terms of conditional coverage and improves the reliability of statistical inference in a wide range of applications.

Efficient Conformal Prediction under Data Heterogeneity

Conformal Prediction (CP) stands out as a robust framework for uncertainty quantification, which is crucial for ensuring the reliability of predictions. However, common CP methods heavily rely on data exchangeability, a condition often violated in practice. Existing approaches for tackling non-exchangeability lead to methods that are not computable beyond the simplest examples. This work introduces a new efficient approach to CP that produces provably valid confidence sets for fairly general non-exchangeable data distributions. We illustrate the general theory with applications to the challenging setting of federated learning under data heterogeneity between agents. Our method allows constructing provably valid personalized prediction sets for agents in a fully federated way. The effectiveness of the proposed method is demonstrated in a series of experiments on real-world datasets.

Conformal Prediction for Federated Uncertainty Quantification Under Label Shift

Federated Learning (FL) is a machine learning framework where many clients collaboratively train models while keeping the training data decentralized. Despite recent advances in FL, the uncertainty quantification topic (UQ) remains partially addressed. Among UQ methods, conformal prediction (CP) approaches provides distribution-free guarantees under minimal assumptions. We develop a new federated conformal prediction method based on quantile regression and take into account privacy constraints. This method takes advantage of importance weighting to effectively address the label shift between agents and provides theoretical guarantees for both valid coverage of the prediction sets and differential privacy. Extensive experimental studies demonstrate that this method outperforms current competitors.

Federated Averaging Langevin Dynamics: Toward a unified theory and new algorithms

This paper focuses on Bayesian inference in a federated learning context (FL). While several distributed MCMC algorithms have been proposed, few consider the specific limitations of FL such as communication bottlenecks and statistical heterogeneity. Recently, Federated Averaging Langevin Dynamics (FALD) was introduced, which extends the Federated Averaging algorithm to Bayesian inference. We obtain a novel tight non-asymptotic upper bound on the Wasserstein distance to the global posterior for FALD. This bound highlights the effects of statistical heterogeneity, which causes a drift in the local updates that negatively impacts convergence. We propose a new algorithm VR-FALD* that uses control variates to correct the client drift. We establish non-asymptotic bounds showing that VR-FALD* is not affected by statistical heterogeneity. Finally, we illustrate our results on several FL benchmarks for Bayesian inference.

Membership Inference Attacks via Adversarial Examples

The raise of machine learning and deep learning led to significant improvement in several domains. This change is supported by both the dramatic rise in computation power and the collection of large datasets. Such massive datasets often include personal data which can represent a threat to privacy. Membership inference attacks are a novel direction of research which aims at recovering training data used by a learning algorithm. In this paper, we develop a mean to measure the leakage of training data leveraging a quantity appearing as a proxy of the total variation of a trained model near its training samples. We extend our work by providing a novel defense mechanism. Our contributions are supported by empirical evidence through convincing numerical experiments.

DG-LMC: A Turn-key and Scalable Synchronous Distributed MCMC Algorithm via Langevin Monte Carlo within Gibbs

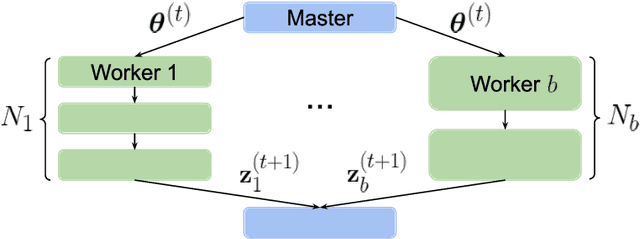
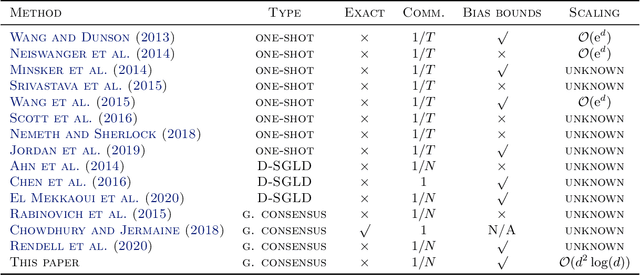
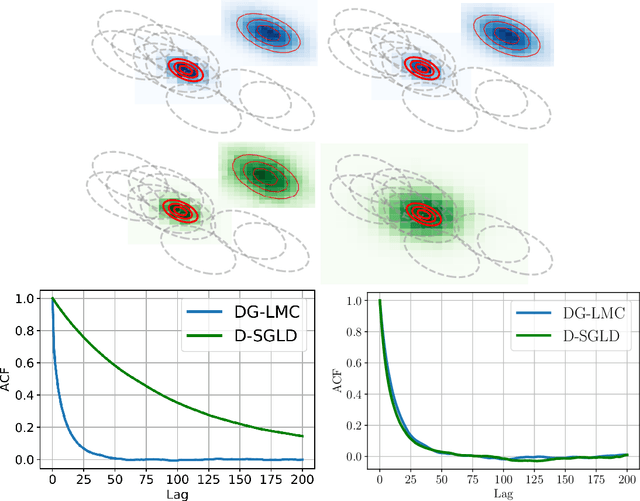
Performing reliable Bayesian inference on a big data scale is becoming a keystone in the modern era of machine learning. A workhorse class of methods to achieve this task are Markov chain Monte Carlo (MCMC) algorithms and their design to handle distributed datasets has been the subject of many works. However, existing methods are not completely either reliable or computationally efficient. In this paper, we propose to fill this gap in the case where the dataset is partitioned and stored on computing nodes within a cluster under a master/slaves architecture. We derive a user-friendly centralised distributed MCMC algorithm with provable scaling in high-dimensional settings. We illustrate the relevance of the proposed methodology on both synthetic and real data experiments.

QLSD: Quantised Langevin stochastic dynamics for Bayesian federated learning

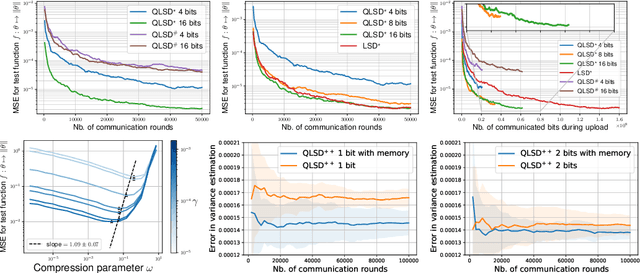
Federated learning aims at conducting inference when data are decentralised and locally stored on several clients, under two main constraints: data ownership and communication overhead. In this paper, we address these issues under the Bayesian paradigm. To this end, we propose a novel Markov chain Monte Carlo algorithm coined \texttt{QLSD} built upon quantised versions of stochastic gradient Langevin dynamics. To improve performance in a big data regime, we introduce variance-reduced alternatives of our methodology referred to as \texttt{QLSD}$^\star$ and \texttt{QLSD}$^{++}$. We provide both non-asymptotic and asymptotic convergence guarantees for the proposed algorithms and illustrate their benefits on several federated learning benchmarks.

Risk bounds when learning infinitely many response functions by ordinary linear regression

Consider the problem of learning a large number of response functions simultaneously based on the same input variables. The training data consist of a single independent random sample of the input variables drawn from a common distribution together with the associated responses. The input variables are mapped into a high-dimensional linear space, called the feature space, and the response functions are modelled as linear functionals of the mapped features, with coefficients calibrated via ordinary least squares. We provide convergence guarantees on the worst-case excess prediction risk by controlling the convergence rate of the excess risk uniformly in the response function. The dimension of the feature map is allowed to tend to infinity with the sample size. The collection of response functions, although potentiallyinfinite, is supposed to have a finite Vapnik-Chervonenkis dimension. The bound derived can be applied when building multiple surrogate models in a reasonable computing time.