Conditionally valid Probabilistic Conformal Prediction
Paper and Code
Jul 01, 2024
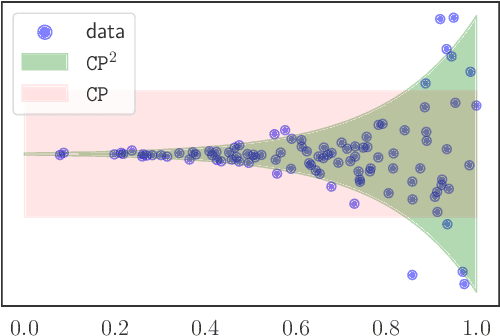
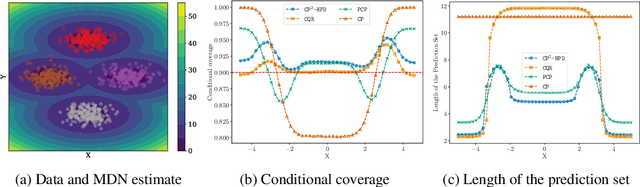
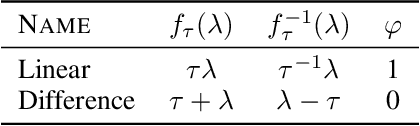
We develop a new method for creating prediction sets that combines the flexibility of conformal methods with an estimate of the conditional distribution $P_{Y \mid X}$. Most existing methods, such as conformalized quantile regression and probabilistic conformal prediction, only offer marginal coverage guarantees. Our approach extends these methods to achieve conditional coverage, which is essential for many practical applications. While exact conditional guarantees are impossible without assumptions on the data distribution, we provide non-asymptotic bounds that explicitly depend on the quality of the available estimate of the conditional distribution. Our confidence sets are highly adaptive to the local structure of the data, making them particularly useful in high heteroskedasticity situations. We demonstrate the effectiveness of our approach through extensive simulations, showing that it outperforms existing methods in terms of conditional coverage and improves the reliability of statistical inference in a wide range of applications.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge