Falcon-H1: A Family of Hybrid-Head Language Models Redefining Efficiency and Performance

In this report, we introduce Falcon-H1, a new series of large language models (LLMs) featuring hybrid architecture designs optimized for both high performance and efficiency across diverse use cases. Unlike earlier Falcon models built solely on Transformer or Mamba architectures, Falcon-H1 adopts a parallel hybrid approach that combines Transformer-based attention with State Space Models (SSMs), known for superior long-context memory and computational efficiency. We systematically revisited model design, data strategy, and training dynamics, challenging conventional practices in the field. Falcon-H1 is released in multiple configurations, including base and instruction-tuned variants at 0.5B, 1.5B, 1.5B-deep, 3B, 7B, and 34B parameters. Quantized instruction-tuned models are also available, totaling over 30 checkpoints on Hugging Face Hub. Falcon-H1 models demonstrate state-of-the-art performance and exceptional parameter and training efficiency. The flagship Falcon-H1-34B matches or outperforms models up to 70B scale, such as Qwen3-32B, Qwen2.5-72B, and Llama3.3-70B, while using fewer parameters and less data. Smaller models show similar trends: the Falcon-H1-1.5B-Deep rivals current leading 7B-10B models, and Falcon-H1-0.5B performs comparably to typical 7B models from 2024. These models excel across reasoning, mathematics, multilingual tasks, instruction following, and scientific knowledge. With support for up to 256K context tokens and 18 languages, Falcon-H1 is suitable for a wide range of applications. All models are released under a permissive open-source license, underscoring our commitment to accessible and impactful AI research.

Falcon Mamba: The First Competitive Attention-free 7B Language Model

In this technical report, we present Falcon Mamba 7B, a new base large language model based on the novel Mamba architecture. Falcon Mamba 7B is trained on 5.8 trillion tokens with carefully selected data mixtures. As a pure Mamba-based model, Falcon Mamba 7B surpasses leading open-weight models based on Transformers, such as Mistral 7B, Llama3.1 8B, and Falcon2 11B. It is on par with Gemma 7B and outperforms models with different architecture designs, such as RecurrentGemma 9B and RWKV-v6 Finch 7B/14B. Currently, Falcon Mamba 7B is the best-performing Mamba model in the literature at this scale, surpassing both existing Mamba and hybrid Mamba-Transformer models, according to the Open LLM Leaderboard. Due to its architecture, Falcon Mamba 7B is significantly faster at inference and requires substantially less memory for long sequence generation. Despite recent studies suggesting that hybrid Mamba-Transformer models outperform pure architecture designs, we demonstrate that even the pure Mamba design can achieve similar, or even superior results compared to the Transformer and hybrid designs. We make the weights of our implementation of Falcon Mamba 7B publicly available on https://huggingface.co/tiiuae/falcon-mamba-7b, under a permissive license.

SGD with memory: fundamental properties and stochastic acceleration

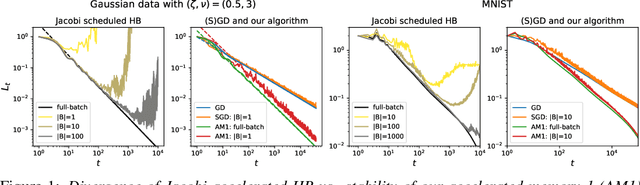
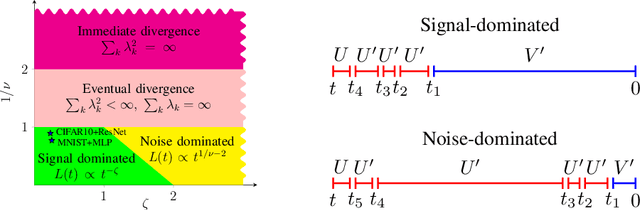
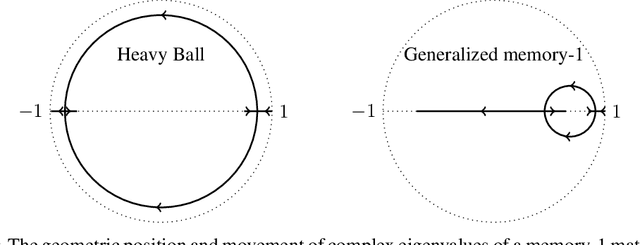
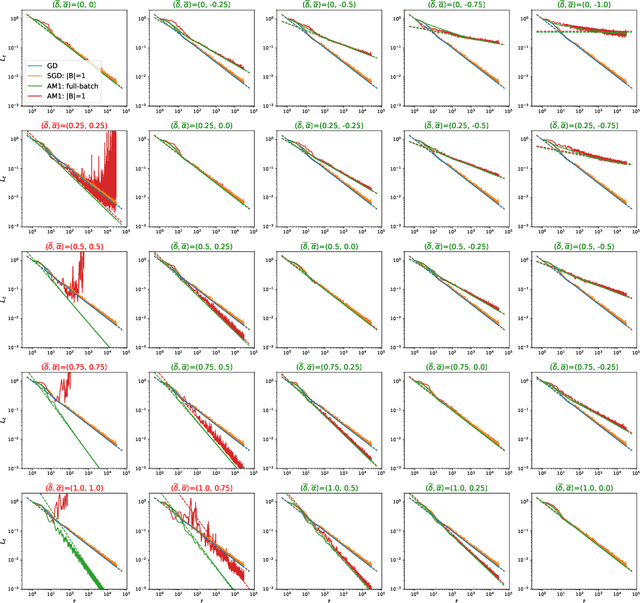
An important open problem is the theoretically feasible acceleration of mini-batch SGD-type algorithms on quadratic problems with power-law spectrum. In the non-stochastic setting, the optimal exponent $\xi$ in the loss convergence $L_t\sim C_Lt^{-\xi}$ is double that in plain GD and is achievable using Heavy Ball (HB) with a suitable schedule; this no longer works in the presence of mini-batch noise. We address this challenge by considering first-order methods with an arbitrary fixed number $M$ of auxiliary velocity vectors (*memory-$M$ algorithms*). We first prove an equivalence between two forms of such algorithms and describe them in terms of suitable characteristic polynomials. Then we develop a general expansion of the loss in terms of signal and noise propagators. Using it, we show that losses of stationary stable memory-$M$ algorithms always retain the exponent $\xi$ of plain GD, but can have different constants $C_L$ depending on their effective learning rate that generalizes that of HB. We prove that in memory-1 algorithms we can make $C_L$ arbitrarily small while maintaining stability. As a consequence, we propose a memory-1 algorithm with a time-dependent schedule that we show heuristically and experimentally to improve the exponent $\xi$ of plain SGD.

Falcon2-11B Technical Report

We introduce Falcon2-11B, a foundation model trained on over five trillion tokens, and its multimodal counterpart, Falcon2-11B-vlm, which is a vision-to-text model. We report our findings during the training of the Falcon2-11B which follows a multi-stage approach where the early stages are distinguished by their context length and a final stage where we use a curated, high-quality dataset. Additionally, we report the effect of doubling the batch size mid-training and how training loss spikes are affected by the learning rate. The downstream performance of the foundation model is evaluated on established benchmarks, including multilingual and code datasets. The foundation model shows strong generalization across all the tasks which makes it suitable for downstream finetuning use cases. For the vision language model, we report the performance on several benchmarks and show that our model achieves a higher average score compared to open-source models of similar size. The model weights and code of both Falcon2-11B and Falcon2-11B-vlm are made available under a permissive license.

Generalization error of spectral algorithms

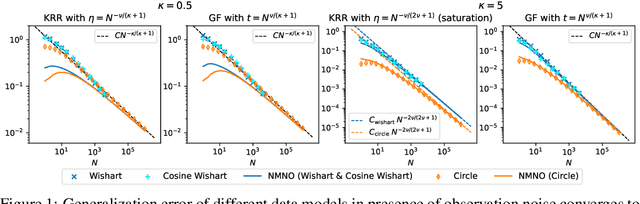
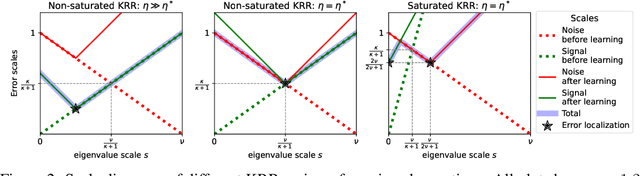
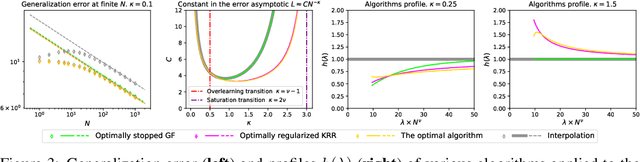
The asymptotically precise estimation of the generalization of kernel methods has recently received attention due to the parallels between neural networks and their associated kernels. However, prior works derive such estimates for training by kernel ridge regression (KRR), whereas neural networks are typically trained with gradient descent (GD). In the present work, we consider the training of kernels with a family of $\textit{spectral algorithms}$ specified by profile $h(\lambda)$, and including KRR and GD as special cases. Then, we derive the generalization error as a functional of learning profile $h(\lambda)$ for two data models: high-dimensional Gaussian and low-dimensional translation-invariant model. Under power-law assumptions on the spectrum of the kernel and target, we use our framework to (i) give full loss asymptotics for both noisy and noiseless observations (ii) show that the loss localizes on certain spectral scales, giving a new perspective on the KRR saturation phenomenon (iii) conjecture, and demonstrate for the considered data models, the universality of the loss w.r.t. non-spectral details of the problem, but only in case of noisy observation.

Efficient Conformal Prediction under Data Heterogeneity

Conformal Prediction (CP) stands out as a robust framework for uncertainty quantification, which is crucial for ensuring the reliability of predictions. However, common CP methods heavily rely on data exchangeability, a condition often violated in practice. Existing approaches for tackling non-exchangeability lead to methods that are not computable beyond the simplest examples. This work introduces a new efficient approach to CP that produces provably valid confidence sets for fairly general non-exchangeable data distributions. We illustrate the general theory with applications to the challenging setting of federated learning under data heterogeneity between agents. Our method allows constructing provably valid personalized prediction sets for agents in a fully federated way. The effectiveness of the proposed method is demonstrated in a series of experiments on real-world datasets.

Comparing the robustness of modern no-reference image- and video-quality metrics to adversarial attacks

Nowadays neural-network-based image- and video-quality metrics show better performance compared to traditional methods. However, they also became more vulnerable to adversarial attacks that increase metrics' scores without improving visual quality. The existing benchmarks of quality metrics compare their performance in terms of correlation with subjective quality and calculation time. However, the adversarial robustness of image-quality metrics is also an area worth researching. In this paper, we analyse modern metrics' robustness to different adversarial attacks. We adopted adversarial attacks from computer vision tasks and compared attacks' efficiency against 15 no-reference image/video-quality metrics. Some metrics showed high resistance to adversarial attacks which makes their usage in benchmarks safer than vulnerable metrics. The benchmark accepts new metrics submissions for researchers who want to make their metrics more robust to attacks or to find such metrics for their needs. Try our benchmark using pip install robustness-benchmark.

A view of mini-batch SGD via generating functions: conditions of convergence, phase transitions, benefit from negative momenta

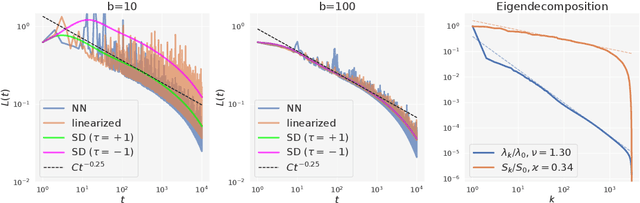
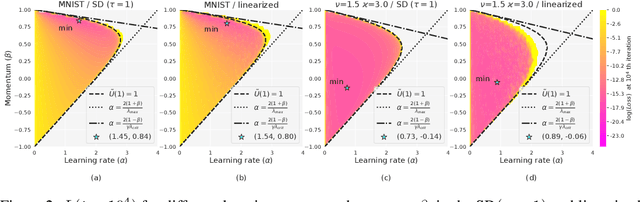
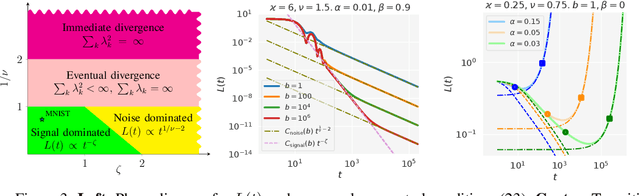
Mini-batch SGD with momentum is a fundamental algorithm for learning large predictive models. In this paper we develop a new analytic framework to analyze mini-batch SGD for linear models at different momenta and sizes of batches. Our key idea is to describe the loss value sequence in terms of its generating function, which can be written in a compact form assuming a diagonal approximation for the second moments of model weights. By analyzing this generating function, we deduce various conclusions on the convergence conditions, phase structure of the model, and optimal learning settings. As a few examples, we show that 1) the optimization trajectory can generally switch from the "signal-dominated" to the "noise-dominated" phase, at a time scale that can be predicted analytically; 2) in the "signal-dominated" (but not the "noise-dominated") phase it is favorable to choose a large effective learning rate, however its value must be limited for any finite batch size to avoid divergence; 3) optimal convergence rate can be achieved at a negative momentum. We verify our theoretical predictions by extensive experiments with MNIST and synthetic problems, and find a good quantitative agreement.

Embedded Ensembles: Infinite Width Limit and Operating Regimes

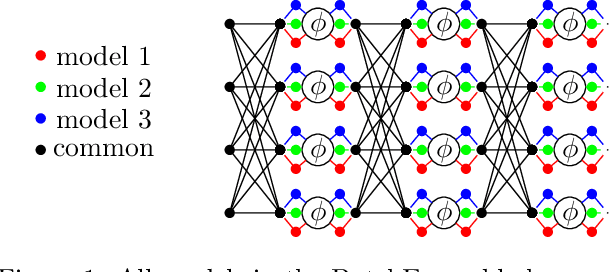
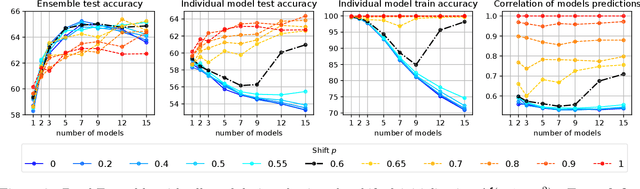
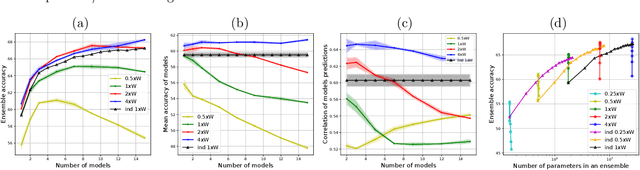
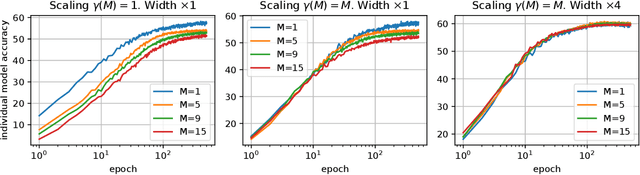
A memory efficient approach to ensembling neural networks is to share most weights among the ensembled models by means of a single reference network. We refer to this strategy as Embedded Ensembling (EE); its particular examples are BatchEnsembles and Monte-Carlo dropout ensembles. In this paper we perform a systematic theoretical and empirical analysis of embedded ensembles with different number of models. Theoretically, we use a Neural-Tangent-Kernel-based approach to derive the wide network limit of the gradient descent dynamics. In this limit, we identify two ensemble regimes - independent and collective - depending on the architecture and initialization strategy of ensemble models. We prove that in the independent regime the embedded ensemble behaves as an ensemble of independent models. We confirm our theoretical prediction with a wide range of experiments with finite networks, and further study empirically various effects such as transition between the two regimes, scaling of ensemble performance with the network width and number of models, and dependence of performance on a number of architecture and hyperparameter choices.

Tight Convergence Rate Bounds for Optimization Under Power Law Spectral Conditions

Performance of optimization on quadratic problems sensitively depends on the low-lying part of the spectrum. For large (effectively infinite-dimensional) problems, this part of the spectrum can often be naturally represented or approximated by power law distributions. In this paper we perform a systematic study of a range of classical single-step and multi-step first order optimization algorithms, with adaptive and non-adaptive, constant and non-constant learning rates: vanilla Gradient Descent, Steepest Descent, Heavy Ball, and Conjugate Gradients. For each of these, we prove that a power law spectral assumption entails a power law for convergence rate of the algorithm, with the convergence rate exponent given by a specific multiple of the spectral exponent. We establish both upper and lower bounds, showing that the results are tight. Finally, we demonstrate applications of these results to kernel learning and training of neural networks in the NTK regime.