A view of mini-batch SGD via generating functions: conditions of convergence, phase transitions, benefit from negative momenta
Paper and Code
Jun 22, 2022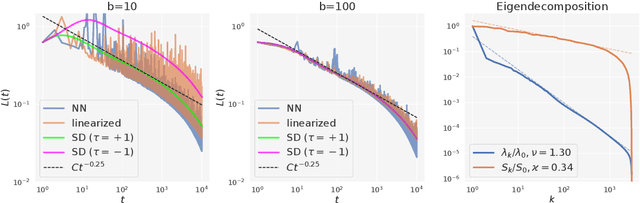
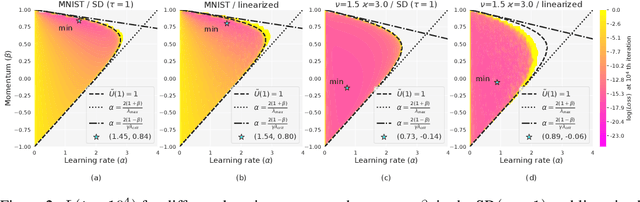
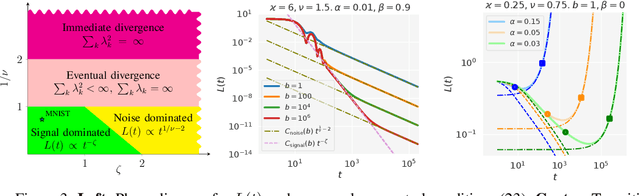

Mini-batch SGD with momentum is a fundamental algorithm for learning large predictive models. In this paper we develop a new analytic framework to analyze mini-batch SGD for linear models at different momenta and sizes of batches. Our key idea is to describe the loss value sequence in terms of its generating function, which can be written in a compact form assuming a diagonal approximation for the second moments of model weights. By analyzing this generating function, we deduce various conclusions on the convergence conditions, phase structure of the model, and optimal learning settings. As a few examples, we show that 1) the optimization trajectory can generally switch from the "signal-dominated" to the "noise-dominated" phase, at a time scale that can be predicted analytically; 2) in the "signal-dominated" (but not the "noise-dominated") phase it is favorable to choose a large effective learning rate, however its value must be limited for any finite batch size to avoid divergence; 3) optimal convergence rate can be achieved at a negative momentum. We verify our theoretical predictions by extensive experiments with MNIST and synthetic problems, and find a good quantitative agreement.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge