MetFlow: A New Efficient Method for Bridging the Gap between Markov Chain Monte Carlo and Variational Inference
Paper and Code
Feb 27, 2020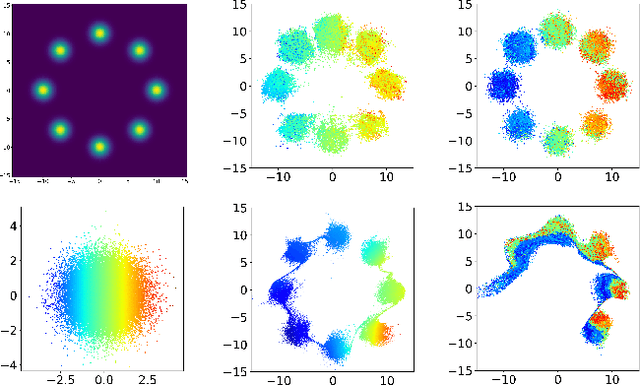
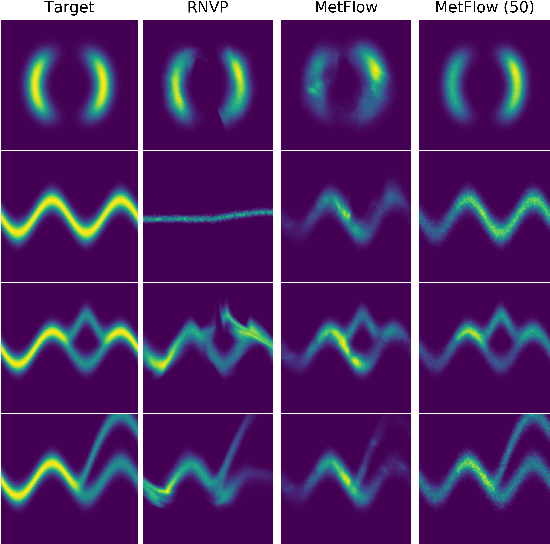


In this contribution, we propose a new computationally efficient method to combine Variational Inference (VI) with Markov Chain Monte Carlo (MCMC). This approach can be used with generic MCMC kernels, but is especially well suited to \textit{MetFlow}, a novel family of MCMC algorithms we introduce, in which proposals are obtained using Normalizing Flows. The marginal distribution produced by such MCMC algorithms is a mixture of flow-based distributions, thus drastically increasing the expressivity of the variational family. Unlike previous methods following this direction, our approach is amenable to the reparametrization trick and does not rely on computationally expensive reverse kernels. Extensive numerical experiments show clear computational and performance improvements over state-of-the-art methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge