Asymptotically exact data augmentation: models, properties and algorithms

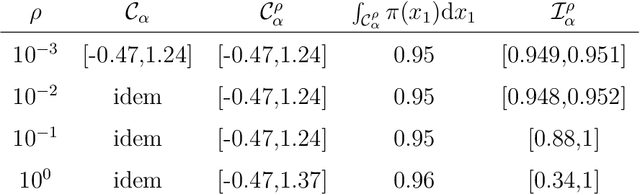
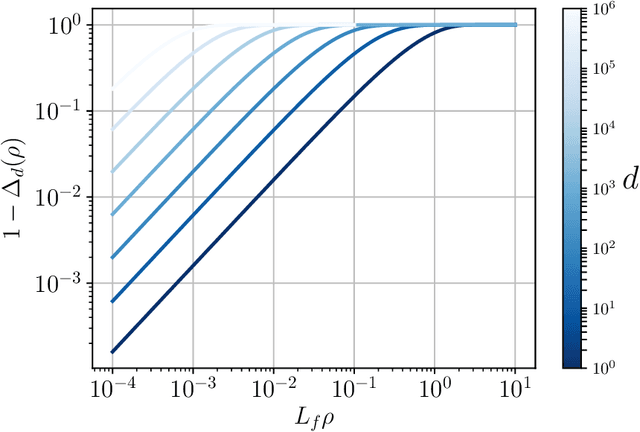
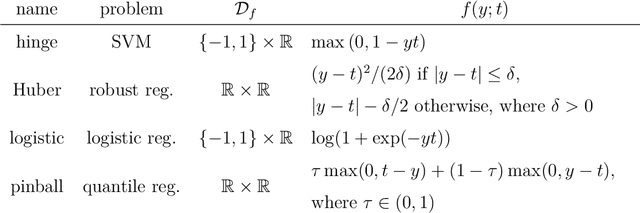
Data augmentation, by the introduction of auxiliary variables, has become an ubiquitous technique to improve mixing/convergence properties, simplify the implementation or reduce the computational time of inference methods such as Markov chain Monte Carlo. Nonetheless, introducing appropriate auxiliary variables while preserving the initial target probability distribution cannot be conducted in a systematic way but highly depends on the considered problem. To deal with such issues, this paper draws a unified framework, namely asymptotically exact data augmentation (AXDA), which encompasses several well-established but also more recent approximate augmented models. Benefiting from a much more general perspective, it delivers some additional qualitative and quantitative insights concerning these schemes. In particular, general properties of AXDA along with non-asymptotic theoretical results on the approximation that is made are stated. Close connections to existing Bayesian methods (e.g. mixture modeling, robust Bayesian models and approximate Bayesian computation) are also drawn. All the results are illustrated with examples and applied to standard statistical learning problems.