Linear Attention with Global Context: A Multipole Attention Mechanism for Vision and Physics

Transformers have become the de facto standard for a wide range of tasks, from image classification to physics simulations. Despite their impressive performance, the quadratic complexity of standard Transformers in both memory and time with respect to the input length makes them impractical for processing high-resolution inputs. Therefore, several variants have been proposed, the most successful relying on patchification, downsampling, or coarsening techniques, often at the cost of losing the finest-scale details. In this work, we take a different approach. Inspired by state-of-the-art techniques in $n$-body numerical simulations, we cast attention as an interaction problem between grid points. We introduce the Multipole Attention Neural Operator (MANO), which computes attention in a distance-based multiscale fashion. MANO maintains, in each attention head, a global receptive field and achieves linear time and memory complexity with respect to the number of grid points. Empirical results on image classification and Darcy flows demonstrate that MANO rivals state-of-the-art models such as ViT and Swin Transformer, while reducing runtime and peak memory usage by orders of magnitude. We open source our code for reproducibility at https://github.com/AlexColagrande/MANO.

Bridging the Theoretical Gap in Randomized Smoothing

Randomized smoothing has become a leading approach for certifying adversarial robustness in machine learning models. However, a persistent gap remains between theoretical certified robustness and empirical robustness accuracy. This paper introduces a new framework that bridges this gap by leveraging Lipschitz continuity for certification and proposing a novel, less conservative method for computing confidence intervals in randomized smoothing. Our approach tightens the bounds of certified robustness, offering a more accurate reflection of model robustness in practice. Through rigorous experimentation we show that our method improves the robust accuracy, compressing the gap between empirical findings and previous theoretical results. We argue that investigating local Lipschitz constants and designing ad-hoc confidence intervals can further enhance the performance of randomized smoothing. These results pave the way for a deeper understanding of the relationship between Lipschitz continuity and certified robustness.

Fast Training of Recurrent Neural Networks with Stationary State Feedbacks

Recurrent neural networks (RNNs) have recently demonstrated strong performance and faster inference than Transformers at comparable parameter budgets. However, the recursive gradient computation with the backpropagation through time (or BPTT) algorithm remains the major computational bottleneck. In this work, we propose a novel method that replaces BPTT with a fixed gradient feedback mechanism, yielding an efficient approximation of the exact gradient propagation based on the assumption of time stationarity. Our approach leverages state-space model (SSM) principles to define a structured feedback matrix that directly propagates gradients from future time steps. This formulation bypasses the need for recursive gradient backpropagation, significantly reducing training overhead while preserving the network's ability to capture long-term dependencies. The experiments on language modeling benchmarks exhibit competitive perplexity scores, while significantly reducing the training costs. These promising results suggest that designing a feedback method like an SSM can fully exploit the efficiency advantages of RNNs for many practical applications.

SCOPE: A Self-supervised Framework for Improving Faithfulness in Conditional Text Generation

Large Language Models (LLMs), when used for conditional text generation, often produce hallucinations, i.e., information that is unfaithful or not grounded in the input context. This issue arises in typical conditional text generation tasks, such as text summarization and data-to-text generation, where the goal is to produce fluent text based on contextual input. When fine-tuned on specific domains, LLMs struggle to provide faithful answers to a given context, often adding information or generating errors. One underlying cause of this issue is that LLMs rely on statistical patterns learned from their training data. This reliance can interfere with the model's ability to stay faithful to a provided context, leading to the generation of ungrounded information. We build upon this observation and introduce a novel self-supervised method for generating a training set of unfaithful samples. We then refine the model using a training process that encourages the generation of grounded outputs over unfaithful ones, drawing on preference-based training. Our approach leads to significantly more grounded text generation, outperforming existing self-supervised techniques in faithfulness, as evaluated through automatic metrics, LLM-based assessments, and human evaluations.

Conditional Distribution Quantization in Machine Learning

Conditional expectation \mathbb{E}(Y \mid X) often fails to capture the complexity of multimodal conditional distributions \mathcal{L}(Y \mid X). To address this, we propose using n-point conditional quantizations--functional mappings of X that are learnable via gradient descent--to approximate \mathcal{L}(Y \mid X). This approach adapts Competitive Learning Vector Quantization (CLVQ), tailored for conditional distributions. It goes beyond single-valued predictions by providing multiple representative points that better reflect multimodal structures. It enables the approximation of the true conditional law in the Wasserstein distance. The resulting framework is theoretically grounded and useful for uncertainty quantification and multimodal data generation tasks. For example, in computer vision inpainting tasks, multiple plausible reconstructions may exist for the same partially observed input image X. We demonstrate the effectiveness of our approach through experiments on synthetic and real-world datasets.

Accelerated Training through Iterative Gradient Propagation Along the Residual Path

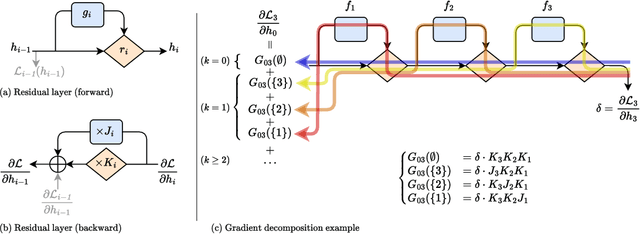
Despite being the cornerstone of deep learning, backpropagation is criticized for its inherent sequentiality, which can limit the scalability of very deep models. Such models faced convergence issues due to vanishing gradient, later resolved using residual connections. Variants of these are now widely used in modern architecture. However, the computational cost of backpropagation remains a major burden, accounting for most of the training time. Taking advantage of residual-like architectural designs, we introduce Highway backpropagation, a parallelizable iterative algorithm that approximates backpropagation, by alternatively i) accumulating the gradient estimates along the residual path, and ii) backpropagating them through every layer in parallel. This algorithm is naturally derived from a decomposition of the gradient as the sum of gradients flowing through all paths and is adaptable to a diverse set of common architectures, ranging from ResNets and Transformers to recurrent neural networks. Through an extensive empirical study on a large selection of tasks and models, we evaluate Highway-BP and show that major speedups can be achieved with minimal performance degradation.

Chain and Causal Attention for Efficient Entity Tracking

This paper investigates the limitations of transformers for entity-tracking tasks in large language models. We identify a theoretical constraint, showing that transformers require at least $\log_2 (n+1)$ layers to handle entity tracking with $n$ state changes. To address this issue, we propose an efficient and frugal enhancement to the standard attention mechanism, enabling it to manage long-term dependencies more efficiently. By considering attention as an adjacency matrix, our model can track entity states with a single layer. Empirical results demonstrate significant improvements in entity tracking datasets while keeping competitive performance on standard natural language modeling. Our modified attention allows us to achieve the same performance with drastically fewer layers. Additionally, our enhanced mechanism reveals structured internal representations of attention. Extensive experiments on both toy and complex datasets validate our approach. Our contributions include theoretical insights, an improved attention mechanism, and empirical validation.

Exploring Precision and Recall to assess the quality and diversity of LLMs

This paper introduces a novel evaluation framework for Large Language Models (LLMs) such as Llama-2 and Mistral, focusing on the adaptation of Precision and Recall metrics from image generation to text generation. This approach allows for a nuanced assessment of the quality and diversity of generated text without the need for aligned corpora. By conducting a comprehensive evaluation of state-of-the-art language models, the study reveals significant insights into their performance on open-ended generation tasks, which are not adequately captured by traditional benchmarks. The findings highlight a trade-off between the quality and diversity of generated samples, particularly when models are fine-tuned with human feedback. This work extends the toolkit for distribution-based NLP evaluation, offering insights into the practical capabilities and challenges faced by current LLMs in generating diverse and high-quality text.

Spectral Norm of Convolutional Layers with Circular and Zero Paddings

This paper leverages the use of \emph{Gram iteration} an efficient, deterministic, and differentiable method for computing spectral norm with an upper bound guarantee. Designed for circular convolutional layers, we generalize the use of the Gram iteration to zero padding convolutional layers and prove its quadratic convergence. We also provide theorems for bridging the gap between circular and zero padding convolution's spectral norm. We design a \emph{spectral rescaling} that can be used as a competitive $1$-Lipschitz layer that enhances network robustness. Demonstrated through experiments, our method outperforms state-of-the-art techniques in precision, computational cost, and scalability. The code of experiments is available at https://github.com/blaisedelattre/lip4conv.

LOCOST: State-Space Models for Long Document Abstractive Summarization

State-space models are a low-complexity alternative to transformers for encoding long sequences and capturing long-term dependencies. We propose LOCOST: an encoder-decoder architecture based on state-space models for conditional text generation with long context inputs. With a computational complexity of $O(L \log L)$, this architecture can handle significantly longer sequences than state-of-the-art models that are based on sparse attention patterns. We evaluate our model on a series of long document abstractive summarization tasks. The model reaches a performance level that is 93-96% comparable to the top-performing sparse transformers of the same size while saving up to 50% memory during training and up to 87% during inference. Additionally, LOCOST effectively handles input texts exceeding 600K tokens at inference time, setting new state-of-the-art results on full-book summarization and opening new perspectives for long input processing.