Yuan Yin
MLIA
Driving on Registers
Jan 08, 2026Abstract:We present DrivoR, a simple and efficient transformer-based architecture for end-to-end autonomous driving. Our approach builds on pretrained Vision Transformers (ViTs) and introduces camera-aware register tokens that compress multi-camera features into a compact scene representation, significantly reducing downstream computation without sacrificing accuracy. These tokens drive two lightweight transformer decoders that generate and then score candidate trajectories. The scoring decoder learns to mimic an oracle and predicts interpretable sub-scores representing aspects such as safety, comfort, and efficiency, enabling behavior-conditioned driving at inference. Despite its minimal design, DrivoR outperforms or matches strong contemporary baselines across NAVSIM-v1, NAVSIM-v2, and the photorealistic closed-loop HUGSIM benchmark. Our results show that a pure-transformer architecture, combined with targeted token compression, is sufficient for accurate, efficient, and adaptive end-to-end driving. Code and checkpoints will be made available via the project page.
IPA: An Information-Preserving Input Projection Framework for Efficient Foundation Model Adaptation
Sep 04, 2025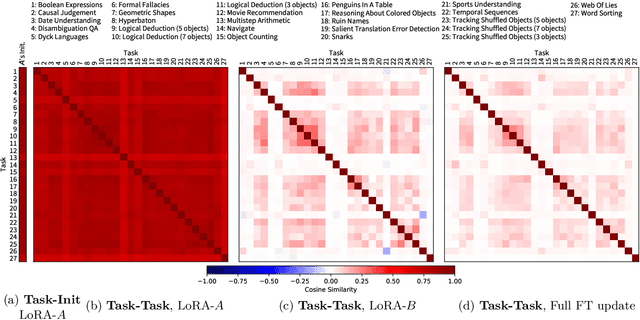
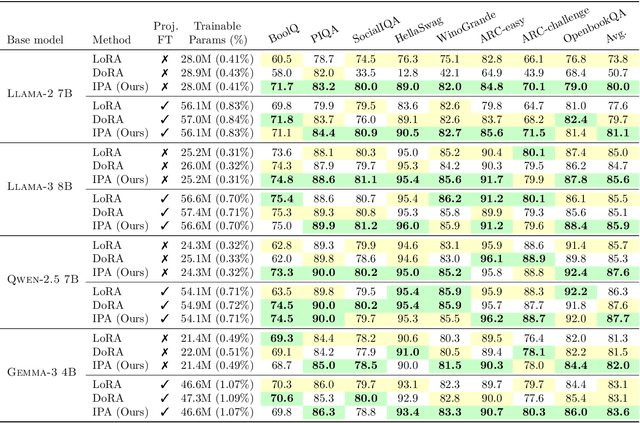
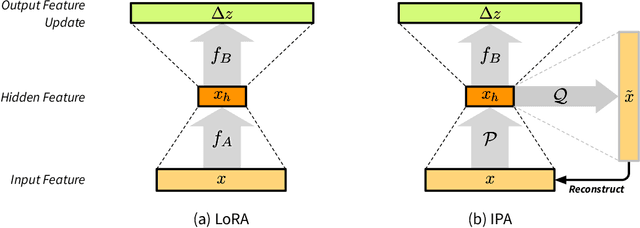
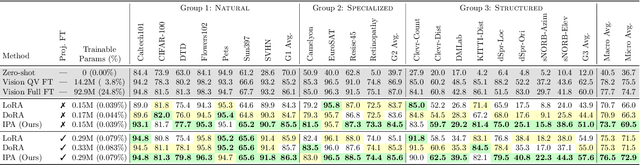
Abstract:Parameter-efficient fine-tuning (PEFT) methods, such as LoRA, reduce adaptation cost by injecting low-rank updates into pretrained weights. However, LoRA's down-projection is randomly initialized and data-agnostic, discarding potentially useful information. Prior analyses show that this projection changes little during training, while the up-projection carries most of the adaptation, making the random input compression a performance bottleneck. We propose IPA, a feature-aware projection framework that explicitly preserves information in the reduced hidden space. In the linear case, we instantiate IPA with algorithms approximating top principal components, enabling efficient projector pretraining with negligible inference overhead. Across language and vision benchmarks, IPA consistently improves over LoRA and DoRA, achieving on average 1.5 points higher accuracy on commonsense reasoning and 2.3 points on VTAB-1k, while matching full LoRA performance with roughly half the trainable parameters when the projection is frozen.
UniCAD: Efficient and Extendable Architecture for Multi-Task Computer-Aided Diagnosis System
May 15, 2025Abstract:The growing complexity and scale of visual model pre-training have made developing and deploying multi-task computer-aided diagnosis (CAD) systems increasingly challenging and resource-intensive. Furthermore, the medical imaging community lacks an open-source CAD platform to enable the rapid creation of efficient and extendable diagnostic models. To address these issues, we propose UniCAD, a unified architecture that leverages the robust capabilities of pre-trained vision foundation models to seamlessly handle both 2D and 3D medical images while requiring only minimal task-specific parameters. UniCAD introduces two key innovations: (1) Efficiency: A low-rank adaptation strategy is employed to adapt a pre-trained visual model to the medical image domain, achieving performance on par with fully fine-tuned counterparts while introducing only 0.17% trainable parameters. (2) Plug-and-Play: A modular architecture that combines a frozen foundation model with multiple plug-and-play experts, enabling diverse tasks and seamless functionality expansion. Building on this unified CAD architecture, we establish an open-source platform where researchers can share and access lightweight CAD experts, fostering a more equitable and efficient research ecosystem. Comprehensive experiments across 12 diverse medical datasets demonstrate that UniCAD consistently outperforms existing methods in both accuracy and deployment efficiency. The source code and project page are available at https://mii-laboratory.github.io/UniCAD/.
Med-LEGO: Editing and Adapting toward Generalist Medical Image Diagnosis
Mar 03, 2025


Abstract:The adoption of visual foundation models has become a common practice in computer-aided diagnosis (CAD). While these foundation models provide a viable solution for creating generalist medical AI, privacy concerns make it difficult to pre-train or continuously update such models across multiple domains and datasets, leading many studies to focus on specialist models. To address this challenge, we propose Med-LEGO, a training-free framework that enables the seamless integration or updating of a generalist CAD model by combining multiple specialist models, similar to assembling LEGO bricks. Med-LEGO enhances LoRA (low-rank adaptation) by incorporating singular value decomposition (SVD) to efficiently capture the domain expertise of each specialist model with minimal additional parameters. By combining these adapted weights through simple operations, Med-LEGO allows for the easy integration or modification of specific diagnostic capabilities without the need for original data or retraining. Finally, the combined model can be further adapted to new diagnostic tasks, making it a versatile generalist model. Our extensive experiments demonstrate that Med-LEGO outperforms existing methods in both cross-domain and in-domain medical tasks while using only 0.18% of full model parameters. These merged models show better convergence and generalization to new tasks, providing an effective path toward generalist medical AI.
PPT: Pre-Training with Pseudo-Labeled Trajectories for Motion Forecasting
Dec 09, 2024Abstract:Motion forecasting (MF) for autonomous driving aims at anticipating trajectories of surrounding agents in complex urban scenarios. In this work, we investigate a mixed strategy in MF training that first pre-train motion forecasters on pseudo-labeled data, then fine-tune them on annotated data. To obtain pseudo-labeled trajectories, we propose a simple pipeline that leverages off-the-shelf single-frame 3D object detectors and non-learning trackers. The whole pre-training strategy including pseudo-labeling is coined as PPT. Our extensive experiments demonstrate that: (1) combining PPT with supervised fine-tuning on annotated data achieves superior performance on diverse testbeds, especially under annotation-efficient regimes, (2) scaling up to multiple datasets improves the previous state-of-the-art and (3) PPT helps enhance cross-dataset generalization. Our findings showcase PPT as a promising pre-training solution for robust motion forecasting in diverse autonomous driving contexts.
GEPS: Boosting Generalization in Parametric PDE Neural Solvers through Adaptive Conditioning
Oct 31, 2024



Abstract:Solving parametric partial differential equations (PDEs) presents significant challenges for data-driven methods due to the sensitivity of spatio-temporal dynamics to variations in PDE parameters. Machine learning approaches often struggle to capture this variability. To address this, data-driven approaches learn parametric PDEs by sampling a very large variety of trajectories with varying PDE parameters. We first show that incorporating conditioning mechanisms for learning parametric PDEs is essential and that among them, $\textit{adaptive conditioning}$, allows stronger generalization. As existing adaptive conditioning methods do not scale well with respect to the number of parameters to adapt in the neural solver, we propose GEPS, a simple adaptation mechanism to boost GEneralization in Pde Solvers via a first-order optimization and low-rank rapid adaptation of a small set of context parameters. We demonstrate the versatility of our approach for both fully data-driven and for physics-aware neural solvers. Validation performed on a whole range of spatio-temporal forecasting problems demonstrates excellent performance for generalizing to unseen conditions including initial conditions, PDE coefficients, forcing terms and solution domain. $\textit{Project page}$: https://geps-project.github.io
Learning a Neural Solver for Parametric PDE to Enhance Physics-Informed Methods
Oct 09, 2024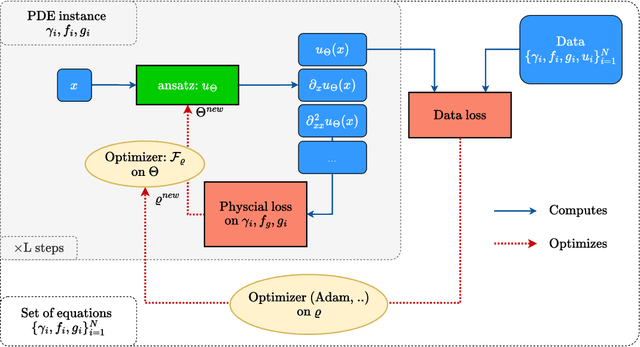

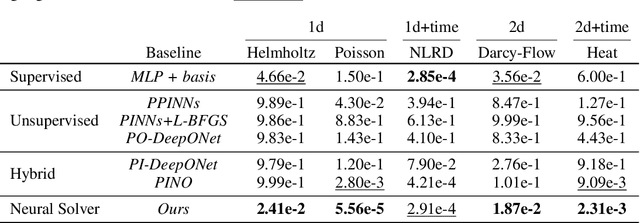
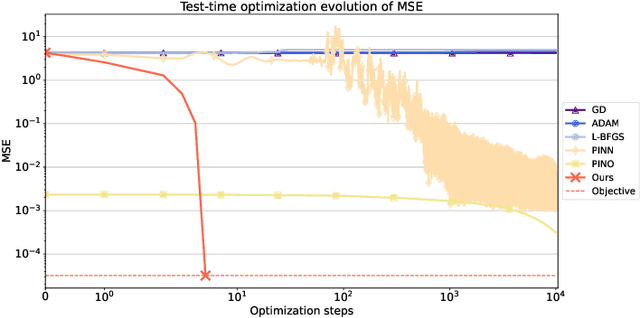
Abstract:Physics-informed deep learning often faces optimization challenges due to the complexity of solving partial differential equations (PDEs), which involve exploring large solution spaces, require numerous iterations, and can lead to unstable training. These challenges arise particularly from the ill-conditioning of the optimization problem, caused by the differential terms in the loss function. To address these issues, we propose learning a solver, i.e., solving PDEs using a physics-informed iterative algorithm trained on data. Our method learns to condition a gradient descent algorithm that automatically adapts to each PDE instance, significantly accelerating and stabilizing the optimization process and enabling faster convergence of physics-aware models. Furthermore, while traditional physics-informed methods solve for a single PDE instance, our approach addresses parametric PDEs. Specifically, our method integrates the physical loss gradient with the PDE parameters to solve over a distribution of PDE parameters, including coefficients, initial conditions, or boundary conditions. We demonstrate the effectiveness of our method through empirical experiments on multiple datasets, comparing training and test-time optimization performance.
ReGentS: Real-World Safety-Critical Driving Scenario Generation Made Stable
Sep 12, 2024Abstract:Machine learning based autonomous driving systems often face challenges with safety-critical scenarios that are rare in real-world data, hindering their large-scale deployment. While increasing real-world training data coverage could address this issue, it is costly and dangerous. This work explores generating safety-critical driving scenarios by modifying complex real-world regular scenarios through trajectory optimization. We propose ReGentS, which stabilizes generated trajectories and introduces heuristics to avoid obvious collisions and optimization problems. Our approach addresses unrealistic diverging trajectories and unavoidable collision scenarios that are not useful for training robust planner. We also extend the scenario generation framework to handle real-world data with up to 32 agents. Additionally, by using a differentiable simulator, our approach simplifies gradient descent-based optimization involving a simulator, paving the way for future advancements. The code is available at https://github.com/valeoai/ReGentS.
Learning to Retrieve for Job Matching
Feb 21, 2024



Abstract:Web-scale search systems typically tackle the scalability challenge with a two-step paradigm: retrieval and ranking. The retrieval step, also known as candidate selection, often involves extracting standardized entities, creating an inverted index, and performing term matching for retrieval. Such traditional methods require manual and time-consuming development of query models. In this paper, we discuss applying learning-to-retrieve technology to enhance LinkedIns job search and recommendation systems. In the realm of promoted jobs, the key objective is to improve the quality of applicants, thereby delivering value to recruiter customers. To achieve this, we leverage confirmed hire data to construct a graph that evaluates a seeker's qualification for a job, and utilize learned links for retrieval. Our learned model is easy to explain, debug, and adjust. On the other hand, the focus for organic jobs is to optimize seeker engagement. We accomplished this by training embeddings for personalized retrieval, fortified by a set of rules derived from the categorization of member feedback. In addition to a solution based on a conventional inverted index, we developed an on-GPU solution capable of supporting both KNN and term matching efficiently.
Proposal-based Temporal Action Localization with Point-level Supervision
Oct 09, 2023



Abstract:Point-level supervised temporal action localization (PTAL) aims at recognizing and localizing actions in untrimmed videos where only a single point (frame) within every action instance is annotated in training data. Without temporal annotations, most previous works adopt the multiple instance learning (MIL) framework, where the input video is segmented into non-overlapped short snippets, and action classification is performed independently on every short snippet. We argue that the MIL framework is suboptimal for PTAL because it operates on separated short snippets that contain limited temporal information. Therefore, the classifier only focuses on several easy-to-distinguish snippets instead of discovering the whole action instance without missing any relevant snippets. To alleviate this problem, we propose a novel method that localizes actions by generating and evaluating action proposals of flexible duration that involve more comprehensive temporal information. Moreover, we introduce an efficient clustering algorithm to efficiently generate dense pseudo labels that provide stronger supervision, and a fine-grained contrastive loss to further refine the quality of pseudo labels. Experiments show that our proposed method achieves competitive or superior performance to the state-of-the-art methods and some fully-supervised methods on four benchmarks: ActivityNet 1.3, THUMOS 14, GTEA, and BEOID datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge