Time Series Continuous Modeling for Imputation and Forecasting with Implicit Neural Representations

Although widely explored, time series modeling continues to encounter significant challenges when confronted with real-world data. We propose a novel modeling approach leveraging Implicit Neural Representations (INR). This approach enables us to effectively capture the continuous aspect of time series and provides a natural solution to recurring modeling issues such as handling missing data, dealing with irregular sampling, or unaligned observations from multiple sensors. By introducing conditional modulation of INR parameters and leveraging meta-learning techniques, we address the issue of generalization to both unseen samples and time window shifts. Through extensive experimentation, our model demonstrates state-of-the-art performance in forecasting and imputation tasks, while exhibiting flexibility in handling a wide range of challenging scenarios that competing models cannot.

Multi-scale Physical Representations for Approximating PDE Solutions with Graph Neural Operators

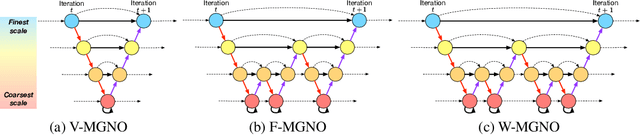
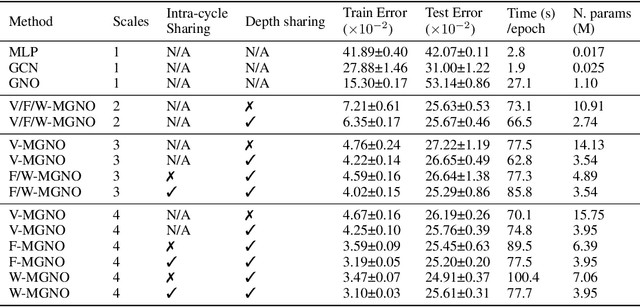
Representing physical signals at different scales is among the most challenging problems in engineering. Several multi-scale modeling tools have been developed to describe physical systems governed by \emph{Partial Differential Equations} (PDEs). These tools are at the crossroad of principled physical models and numerical schema. Recently, data-driven models have been introduced to speed-up the approximation of PDE solutions compared to numerical solvers. Among these recent data-driven methods, neural integral operators are a class that learn a mapping between function spaces. These functions are discretized on graphs (meshes) which are appropriate for modeling interactions in physical phenomena. In this work, we study three multi-resolution schema with integral kernel operators that can be approximated with \emph{Message Passing Graph Neural Networks} (MPGNNs). To validate our study, we make extensive MPGNNs experiments with well-chosen metrics considering steady and unsteady PDEs.