NeurIPS 2024 ML4CFD Competition: Harnessing Machine Learning for Computational Fluid Dynamics in Airfoil Design

The integration of machine learning (ML) techniques for addressing intricate physics problems is increasingly recognized as a promising avenue for expediting simulations. However, assessing ML-derived physical models poses a significant challenge for their adoption within industrial contexts. This competition is designed to promote the development of innovative ML approaches for tackling physical challenges, leveraging our recently introduced unified evaluation framework known as Learning Industrial Physical Simulations (LIPS). Building upon the preliminary edition held from November 2023 to March 2024, this iteration centers on a task fundamental to a well-established physical application: airfoil design simulation, utilizing our proposed AirfRANS dataset. The competition evaluates solutions based on various criteria encompassing ML accuracy, computational efficiency, Out-Of-Distribution performance, and adherence to physical principles. Notably, this competition represents a pioneering effort in exploring ML-driven surrogate methods aimed at optimizing the trade-off between computational efficiency and accuracy in physical simulations. Hosted on the Codabench platform, the competition offers online training and evaluation for all participating solutions.

ML4PhySim : Machine Learning for Physical Simulations Challenge (The airfoil design)

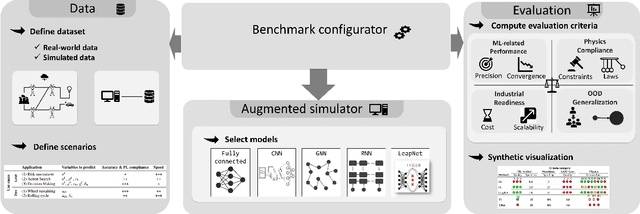
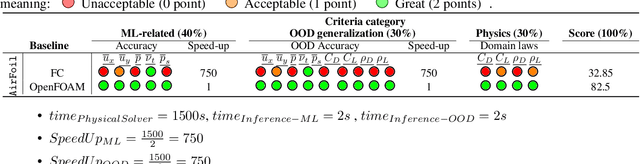
The use of machine learning (ML) techniques to solve complex physical problems has been considered recently as a promising approach. However, the evaluation of such learned physical models remains an important issue for industrial use. The aim of this competition is to encourage the development of new ML techniques to solve physical problems using a unified evaluation framework proposed recently, called Learning Industrial Physical Simulations (LIPS). We propose learning a task representing a well-known physical use case: the airfoil design simulation, using a dataset called AirfRANS. The global score calculated for each submitted solution is based on three main categories of criteria covering different aspects, namely: ML-related, Out-Of-Distribution, and physical compliance criteria. To the best of our knowledge, this is the first competition addressing the use of ML-based surrogate approaches to improve the trade-off computational cost/accuracy of physical simulation.The competition is hosted by the Codabench platform with online training and evaluation of all submitted solutions.

INFINITY: Neural Field Modeling for Reynolds-Averaged Navier-Stokes Equations

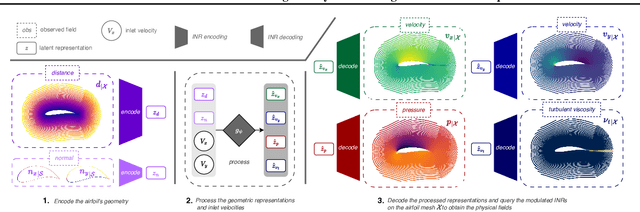
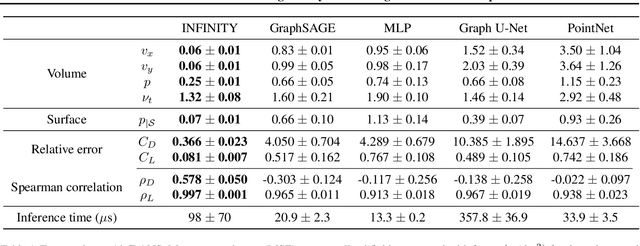
For numerical design, the development of efficient and accurate surrogate models is paramount. They allow us to approximate complex physical phenomena, thereby reducing the computational burden of direct numerical simulations. We propose INFINITY, a deep learning model that utilizes implicit neural representations (INRs) to address this challenge. Our framework encodes geometric information and physical fields into compact representations and learns a mapping between them to infer the physical fields. We use an airfoil design optimization problem as an example task and we evaluate our approach on the challenging AirfRANS dataset, which closely resembles real-world industrial use-cases. The experimental results demonstrate that our framework achieves state-of-the-art performance by accurately inferring physical fields throughout the volume and surface. Additionally we demonstrate its applicability in contexts such as design exploration and shape optimization: our model can correctly predict drag and lift coefficients while adhering to the equations.

Multi-Objective Hull Form Optimization with CAD Engine-based Deep Learning Physics for 3D Flow Prediction

In this work, we propose a built-in Deep Learning Physics Optimization (DLPO) framework to set up a shape optimization study of the Duisburg Test Case (DTC) container vessel. We present two different applications: (1) sensitivity analysis to detect the most promising generic basis hull shapes, and (2) multi-objective optimization to quantify the trade-off between optimal hull forms. DLPO framework allows for the evaluation of design iterations automatically in an end-to-end manner. We achieved these results by coupling Extrality's Deep Learning Physics (DLP) model to a CAD engine and an optimizer. Our proposed DLP model is trained on full 3D volume data coming from RANS simulations, and it can provide accurate and high-quality 3D flow predictions in real-time, which makes it a good evaluator to perform optimization of new container vessel designs w.r.t the hydrodynamic efficiency. In particular, it is able to recover the forces acting on the vessel by integration on the hull surface with a mean relative error of 3.84\% \pm 2.179\% on the total resistance. Each iteration takes only 20 seconds, thus leading to a drastic saving of time and engineering efforts, while delivering valuable insight into the performance of the vessel, including RANS-like detailed flow information. We conclude that DLPO framework is a promising tool to accelerate the ship design process and lead to more efficient ships with better hydrodynamic performance.

An extensible Benchmarking Graph-Mesh dataset for studying Steady-State Incompressible Navier-Stokes Equations

Recent progress in \emph{Geometric Deep Learning} (GDL) has shown its potential to provide powerful data-driven models. This gives momentum to explore new methods for learning physical systems governed by \emph{Partial Differential Equations} (PDEs) from Graph-Mesh data. However, despite the efforts and recent achievements, several research directions remain unexplored and progress is still far from satisfying the physical requirements of real-world phenomena. One of the major impediments is the absence of benchmarking datasets and common physics evaluation protocols. In this paper, we propose a 2-D graph-mesh dataset to study the airflow over airfoils at high Reynolds regime (from $10^6$ and beyond). We also introduce metrics on the stress forces over the airfoil in order to evaluate GDL models on important physical quantities. Moreover, we provide extensive GDL baselines.

Multi-scale Physical Representations for Approximating PDE Solutions with Graph Neural Operators

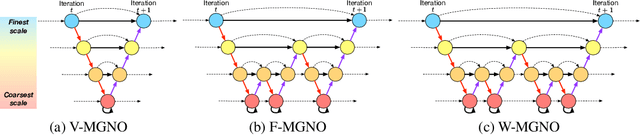
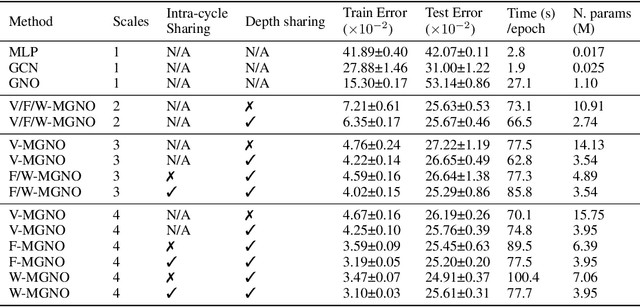
Representing physical signals at different scales is among the most challenging problems in engineering. Several multi-scale modeling tools have been developed to describe physical systems governed by \emph{Partial Differential Equations} (PDEs). These tools are at the crossroad of principled physical models and numerical schema. Recently, data-driven models have been introduced to speed-up the approximation of PDE solutions compared to numerical solvers. Among these recent data-driven methods, neural integral operators are a class that learn a mapping between function spaces. These functions are discretized on graphs (meshes) which are appropriate for modeling interactions in physical phenomena. In this work, we study three multi-resolution schema with integral kernel operators that can be approximated with \emph{Message Passing Graph Neural Networks} (MPGNNs). To validate our study, we make extensive MPGNNs experiments with well-chosen metrics considering steady and unsteady PDEs.