INFINITY: Neural Field Modeling for Reynolds-Averaged Navier-Stokes Equations

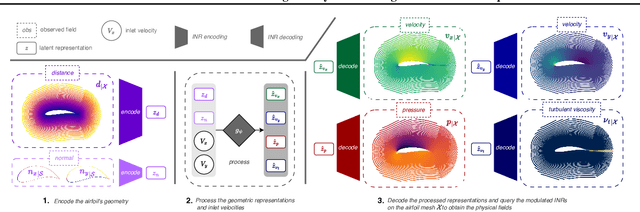
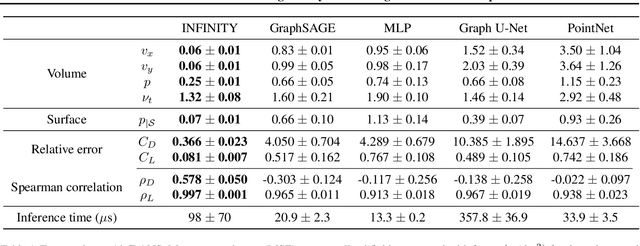
For numerical design, the development of efficient and accurate surrogate models is paramount. They allow us to approximate complex physical phenomena, thereby reducing the computational burden of direct numerical simulations. We propose INFINITY, a deep learning model that utilizes implicit neural representations (INRs) to address this challenge. Our framework encodes geometric information and physical fields into compact representations and learns a mapping between them to infer the physical fields. We use an airfoil design optimization problem as an example task and we evaluate our approach on the challenging AirfRANS dataset, which closely resembles real-world industrial use-cases. The experimental results demonstrate that our framework achieves state-of-the-art performance by accurately inferring physical fields throughout the volume and surface. Additionally we demonstrate its applicability in contexts such as design exploration and shape optimization: our model can correctly predict drag and lift coefficients while adhering to the equations.

Stability of implicit neural networks for long-term forecasting in dynamical systems

Forecasting physical signals in long time range is among the most challenging tasks in Partial Differential Equations (PDEs) research. To circumvent limitations of traditional solvers, many different Deep Learning methods have been proposed. They are all based on auto-regressive methods and exhibit stability issues. Drawing inspiration from the stability property of implicit numerical schemes, we introduce a stable auto-regressive implicit neural network. We develop a theory based on the stability definition of schemes to ensure the stability in forecasting of this network. It leads us to introduce hard constraints on its weights and propagate the dynamics in the latent space. Our experimental results validate our stability property, and show improved results at long-term forecasting for two transports PDEs.