NeurIPS 2024 ML4CFD Competition: Harnessing Machine Learning for Computational Fluid Dynamics in Airfoil Design

The integration of machine learning (ML) techniques for addressing intricate physics problems is increasingly recognized as a promising avenue for expediting simulations. However, assessing ML-derived physical models poses a significant challenge for their adoption within industrial contexts. This competition is designed to promote the development of innovative ML approaches for tackling physical challenges, leveraging our recently introduced unified evaluation framework known as Learning Industrial Physical Simulations (LIPS). Building upon the preliminary edition held from November 2023 to March 2024, this iteration centers on a task fundamental to a well-established physical application: airfoil design simulation, utilizing our proposed AirfRANS dataset. The competition evaluates solutions based on various criteria encompassing ML accuracy, computational efficiency, Out-Of-Distribution performance, and adherence to physical principles. Notably, this competition represents a pioneering effort in exploring ML-driven surrogate methods aimed at optimizing the trade-off between computational efficiency and accuracy in physical simulations. Hosted on the Codabench platform, the competition offers online training and evaluation for all participating solutions.

ML4PhySim : Machine Learning for Physical Simulations Challenge (The airfoil design)

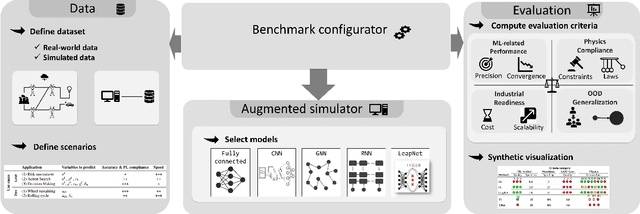
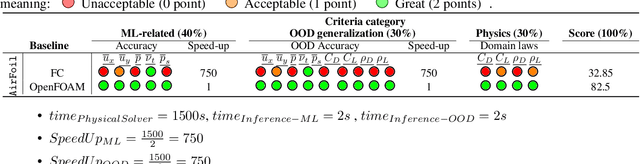
The use of machine learning (ML) techniques to solve complex physical problems has been considered recently as a promising approach. However, the evaluation of such learned physical models remains an important issue for industrial use. The aim of this competition is to encourage the development of new ML techniques to solve physical problems using a unified evaluation framework proposed recently, called Learning Industrial Physical Simulations (LIPS). We propose learning a task representing a well-known physical use case: the airfoil design simulation, using a dataset called AirfRANS. The global score calculated for each submitted solution is based on three main categories of criteria covering different aspects, namely: ML-related, Out-Of-Distribution, and physical compliance criteria. To the best of our knowledge, this is the first competition addressing the use of ML-based surrogate approaches to improve the trade-off computational cost/accuracy of physical simulation.The competition is hosted by the Codabench platform with online training and evaluation of all submitted solutions.

An operator preconditioning perspective on training in physics-informed machine learning

In this paper, we investigate the behavior of gradient descent algorithms in physics-informed machine learning methods like PINNs, which minimize residuals connected to partial differential equations (PDEs). Our key result is that the difficulty in training these models is closely related to the conditioning of a specific differential operator. This operator, in turn, is associated to the Hermitian square of the differential operator of the underlying PDE. If this operator is ill-conditioned, it results in slow or infeasible training. Therefore, preconditioning this operator is crucial. We employ both rigorous mathematical analysis and empirical evaluations to investigate various strategies, explaining how they better condition this critical operator, and consequently improve training.

Graph Neural Networks for Airfoil Design

The study of partial differential equations (PDE) through the framework of deep learning emerged a few years ago leading to the impressive approximations of simple dynamics. Graph neural networks (GNN) turned out to be very useful in those tasks by allowing the treatment of unstructured data often encountered in the field of numerical resolutions of PDE. However, the resolutions of harder PDE such as Navier-Stokes equations are still a challenging task and most of the work done on the latter concentrate either on simulating the flow around simple geometries or on qualitative results that looks physical for design purpose. In this study, we try to leverage the work done on deep learning for PDE and GNN by proposing an adaptation of a known architecture in order to tackle the task of approximating the solution of the two-dimensional steady-state incompressible Navier-Stokes equations over different airfoil geometries. In addition to that, we test our model not only on its performance over the volume but also on its performance to approximate surface quantities such as the wall shear stress or the isostatic pressure leading to the inference of global coefficients such as the lift and the drag of our airfoil in order to allow design exploration. This work takes place in a longer project that aims to approximate three dimensional steady-state solutions over industrial geometries.

AirfRANS: High Fidelity Computational Fluid Dynamics Dataset for Approximating Reynolds-Averaged Navier-Stokes Solutions

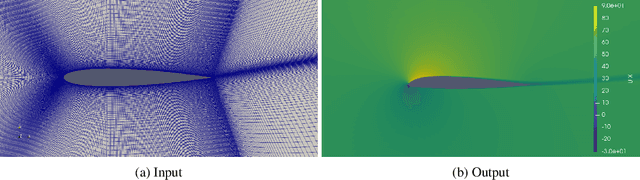
Surrogate models are necessary to optimize meaningful quantities in physical dynamics as their recursive numerical resolutions are often prohibitively expensive. It is mainly the case for fluid dynamics and the resolution of Navier-Stokes equations. However, despite the fast-growing field of data-driven models for physical systems, reference datasets representing real-world phenomena are lacking. In this work, we develop AirfRANS, a dataset for studying the two-dimensional incompressible steady-state Reynolds-Averaged Navier-Stokes equations over airfoils at a subsonic regime and for different angles of attacks. We also introduce metrics on the stress forces at the surface of geometries and visualization of boundary layers to assess the capabilities of models to accurately predict the meaningful information of the problem. Finally, we propose deep learning baselines on four machine learning tasks to study AirfRANS under different constraints for generalization considerations: big and scarce data regime, Reynolds number, and angle of attack extrapolation.

An extensible Benchmarking Graph-Mesh dataset for studying Steady-State Incompressible Navier-Stokes Equations

Recent progress in \emph{Geometric Deep Learning} (GDL) has shown its potential to provide powerful data-driven models. This gives momentum to explore new methods for learning physical systems governed by \emph{Partial Differential Equations} (PDEs) from Graph-Mesh data. However, despite the efforts and recent achievements, several research directions remain unexplored and progress is still far from satisfying the physical requirements of real-world phenomena. One of the major impediments is the absence of benchmarking datasets and common physics evaluation protocols. In this paper, we propose a 2-D graph-mesh dataset to study the airflow over airfoils at high Reynolds regime (from $10^6$ and beyond). We also introduce metrics on the stress forces over the airfoil in order to evaluate GDL models on important physical quantities. Moreover, we provide extensive GDL baselines.