Poseidon: Efficient Foundation Models for PDEs

We introduce Poseidon, a foundation model for learning the solution operators of PDEs. It is based on a multiscale operator transformer, with time-conditioned layer norms that enable continuous-in-time evaluations. A novel training strategy leveraging the semi-group property of time-dependent PDEs to allow for significant scaling-up of the training data is also proposed. Poseidon is pretrained on a diverse, large scale dataset for the governing equations of fluid dynamics. It is then evaluated on a suite of 15 challenging downstream tasks that include a wide variety of PDE types and operators. We show that Poseidon exhibits excellent performance across the board by outperforming baselines significantly, both in terms of sample efficiency and accuracy. Poseidon also generalizes very well to new physics that is not seen during pretraining. Moreover, Poseidon scales with respect to model and data size, both for pretraining and for downstream tasks. Taken together, our results showcase the surprising ability of Poseidon to learn effective representations from a very small set of PDEs during pretraining in order to generalize well to unseen and unrelated PDEs downstream, demonstrating its potential as an effective, general purpose PDE foundation model. Finally, the Poseidon model as well as underlying pretraining and downstream datasets are open sourced, with code being available at https://github.com/camlab-ethz/poseidon and pretrained models and datasets at https://huggingface.co/camlab-ethz.

An operator preconditioning perspective on training in physics-informed machine learning

In this paper, we investigate the behavior of gradient descent algorithms in physics-informed machine learning methods like PINNs, which minimize residuals connected to partial differential equations (PDEs). Our key result is that the difficulty in training these models is closely related to the conditioning of a specific differential operator. This operator, in turn, is associated to the Hermitian square of the differential operator of the underlying PDE. If this operator is ill-conditioned, it results in slow or infeasible training. Therefore, preconditioning this operator is crucial. We employ both rigorous mathematical analysis and empirical evaluations to investigate various strategies, explaining how they better condition this critical operator, and consequently improve training.

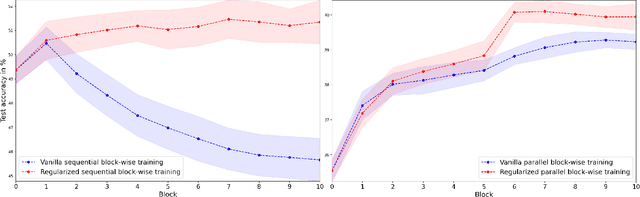
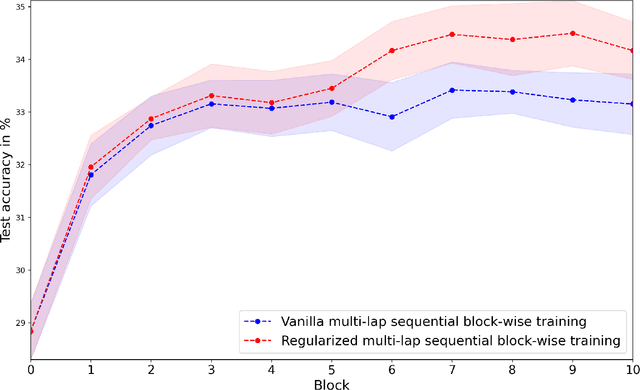
Module-wise Training of Neural Networks via the Minimizing Movement Scheme

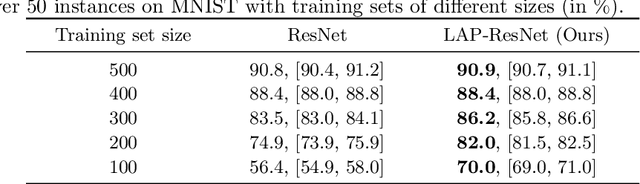
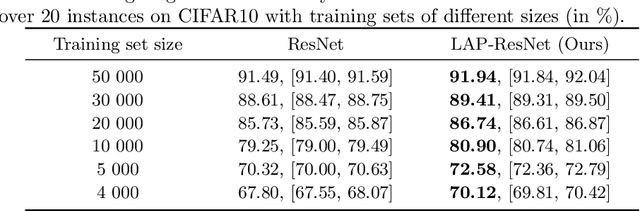
Greedy layer-wise or module-wise training of neural networks is compelling in constrained and on-device settings where memory is limited, as it circumvents a number of problems of end-to-end back-propagation. However, it suffers from a stagnation problem, whereby early layers overfit and deeper layers stop increasing the test accuracy after a certain depth. We propose to solve this issue by introducing a module-wise regularization inspired by the minimizing movement scheme for gradient flows in distribution space. We call the method TRGL for Transport Regularized Greedy Learning and study it theoretically, proving that it leads to greedy modules that are regular and that progressively solve the task. Experimentally, we show improved accuracy of module-wise training of various architectures such as ResNets, Transformers and VGG, when our regularization is added, superior to that of other module-wise training methods and often to end-to-end training, with as much as 60% less memory usage.

Are Neural Operators Really Neural Operators? Frame Theory Meets Operator Learning

Recently, there has been significant interest in operator learning, i.e. learning mappings between infinite-dimensional function spaces. This has been particularly relevant in the context of learning partial differential equations from data. However, it has been observed that proposed models may not behave as operators when implemented on a computer, questioning the very essence of what operator learning should be. We contend that in addition to defining the operator at the continuous level, some form of continuous-discrete equivalence is necessary for an architecture to genuinely learn the underlying operator, rather than just discretizations of it. To this end, we propose to employ frames, a concept in applied harmonic analysis and signal processing that gives rise to exact and stable discrete representations of continuous signals. Extending these concepts to operators, we introduce a unifying mathematical framework of Representation equivalent Neural Operator (ReNO) to ensure operations at the continuous and discrete level are equivalent. Lack of this equivalence is quantified in terms of aliasing errors. We analyze various existing operator learning architectures to determine whether they fall within this framework, and highlight implications when they fail to do so.

Unifying GANs and Score-Based Diffusion as Generative Particle Models

Particle-based deep generative models, such as gradient flows and score-based diffusion models, have recently gained traction thanks to their striking performance. Their principle of displacing particle distributions by differential equations is conventionally seen as opposed to the previously widespread generative adversarial networks (GANs), which involve training a pushforward generator network. In this paper, we challenge this interpretation and propose a novel framework that unifies particle and adversarial generative models by framing generator training as a generalization of particle models. This suggests that a generator is an optional addition to any such generative model. Consequently, integrating a generator into a score-based diffusion model and training a GAN without a generator naturally emerge from our framework. We empirically test the viability of these original models as proofs of concepts of potential applications of our framework.

Module-wise Training of Residual Networks via the Minimizing Movement Scheme

Greedy layer-wise or module-wise training of neural networks is compelling in constrained and on-device settings, as it circumvents a number of problems of end-to-end back-propagation. However, it suffers from a stagnation problem, whereby early layers overfit and deeper layers stop increasing the test accuracy after a certain depth. We propose to solve this issue by introducing a simple module-wise regularization inspired by the minimizing movement scheme for gradient flows in distribution space. The method, which we call TRGL for Transport Regularized Greedy Learning, is particularly well-adapted to residual networks. We study it theoretically, proving that it leads to greedy modules that are regular and that successively solve the task. Experimentally, we show improved accuracy of module-wise trained networks when our regularization is added.

A Neural Tangent Kernel Perspective of GANs

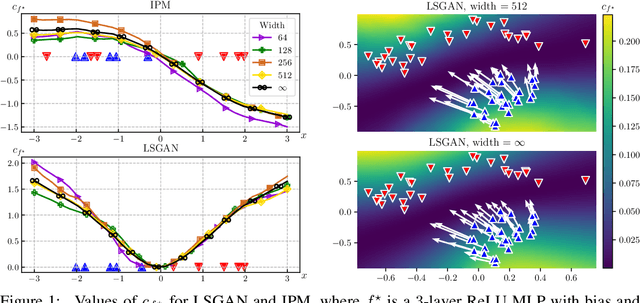
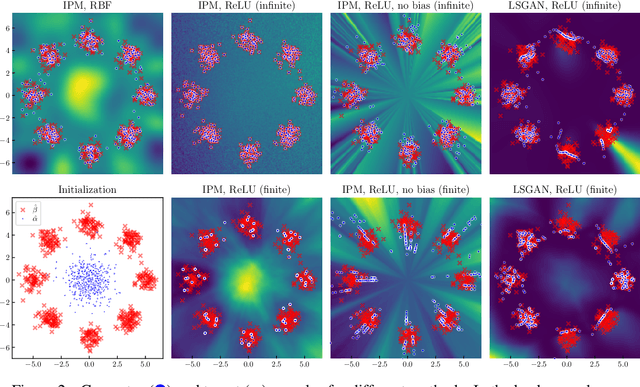
Theoretical analyses for Generative Adversarial Networks (GANs) generally assume an arbitrarily large family of discriminators and do not consider the characteristics of the architectures used in practice. We show that this framework of analysis is too simplistic to properly analyze GAN training. To tackle this issue, we leverage the theory of infinite-width neural networks to model neural discriminator training for a wide range of adversarial losses via its Neural Tangent Kernel (NTK). Our analytical results show that GAN trainability primarily depends on the discriminator's architecture. We further study the discriminator for specific architectures and losses, and highlight properties providing a new understanding of GAN training. For example, we find that GANs trained with the integral probability metric loss minimize the maximum mean discrepancy with the NTK as kernel. Our conclusions demonstrate the analysis opportunities provided by the proposed framework, which paves the way for better and more principled GAN models. We release a generic GAN analysis toolkit based on our framework that supports the empirical part of our study.

LEADS: Learning Dynamical Systems that Generalize Across Environments

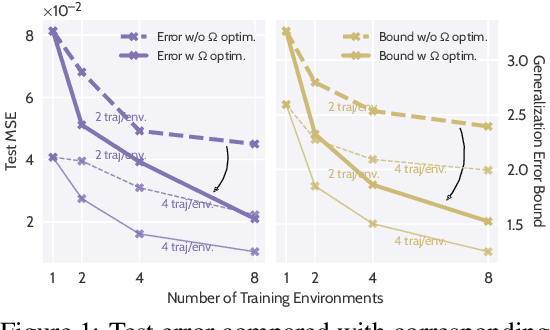
When modeling dynamical systems from real-world data samples, the distribution of data often changes according to the environment in which they are captured, and the dynamics of the system itself vary from one environment to another. Generalizing across environments thus challenges the conventional frameworks. The classical settings suggest either considering data as i.i.d. and learning a single model to cover all situations or learning environment-specific models. Both are sub-optimal: the former disregards the discrepancies between environments leading to biased solutions, while the latter does not exploit their potential commonalities and is prone to scarcity problems. We propose LEADS, a novel framework that leverages the commonalities and discrepancies among known environments to improve model generalization. This is achieved with a tailored training formulation aiming at capturing common dynamics within a shared model while additional terms capture environment-specific dynamics. We ground our approach in theory, exhibiting a decrease in sample complexity with our approach and corroborate these results empirically, instantiating it for linear dynamics. Moreover, we concretize this framework for neural networks and evaluate it experimentally on representative families of nonlinear dynamics. We show that this new setting can exploit knowledge extracted from environment-dependent data and improves generalization for both known and novel environments.

Augmenting Physical Models with Deep Networks for Complex Dynamics Forecasting

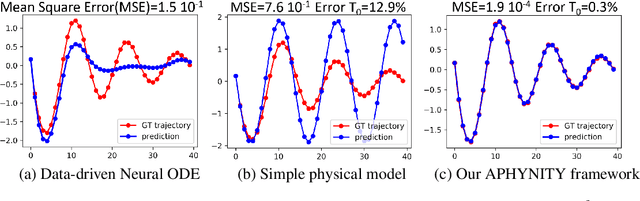
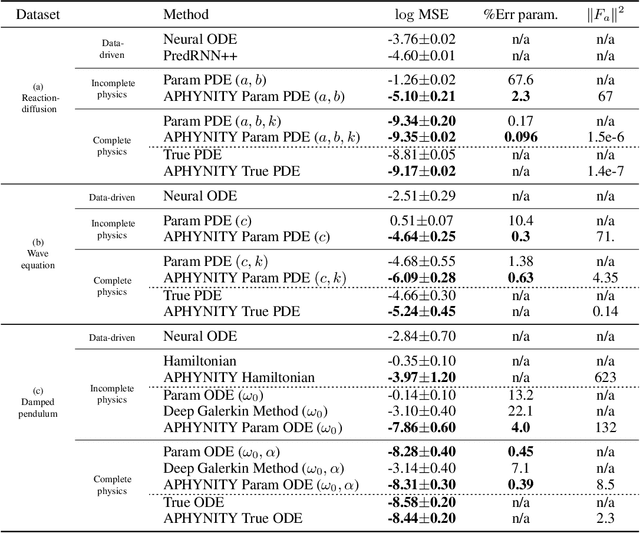
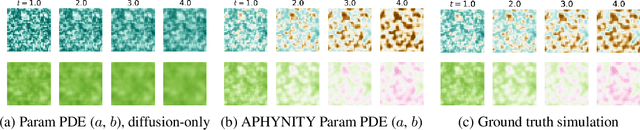
Forecasting complex dynamical phenomena in settings where only partial knowledge of their dynamics is available is a prevalent problem across various scientific fields. While purely data-driven approaches are arguably insufficient in this context, standard physical modeling based approaches tend to be over-simplistic, inducing non-negligible errors. In this work, we introduce the APHYNITY framework, a principled approach for augmenting incomplete physical dynamics described by differential equations with deep data-driven models. It consists in decomposing the dynamics into two components: a physical component accounting for the dynamics for which we have some prior knowledge, and a data-driven component accounting for errors of the physical model. The learning problem is carefully formulated such that the physical model explains as much of the data as possible, while the data-driven component only describes information that cannot be captured by the physical model, no more, no less. This not only provides the existence and uniqueness for this decomposition, but also ensures interpretability and benefits generalization. Experiments made on three important use cases, each representative of a different family of phenomena, i.e. reaction-diffusion equations, wave equations and the non-linear damped pendulum, show that APHYNITY can efficiently leverage approximate physical models to accurately forecast the evolution of the system and correctly identify relevant physical parameters.

A Principle of Least Action for the Training of Neural Networks

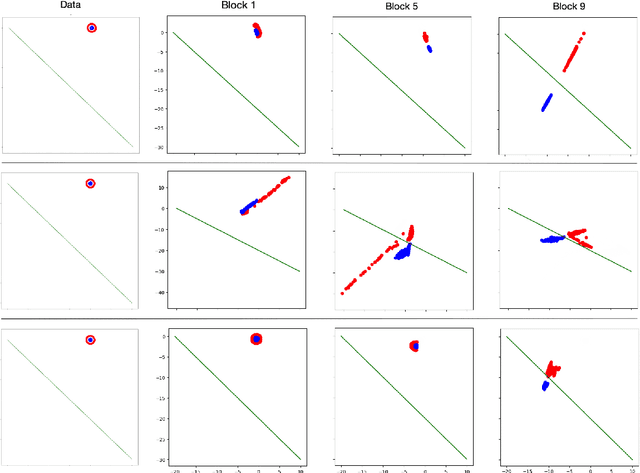
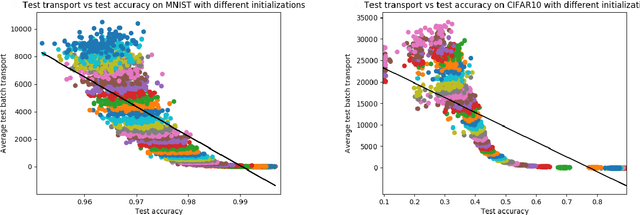
Neural networks have been achieving high generalization performance on many tasks despite being highly over-parameterized. Since classical statistical learning theory struggles to explain this behavior, much effort has recently been focused on uncovering the mechanisms behind it, in the hope of developing a more adequate theoretical framework and having a better control over the trained models. In this work, we adopt an alternate perspective, viewing the neural network as a dynamical system displacing input particles over time. We conduct a series of experiments and, by analyzing the network's behavior through its displacements, we show the presence of a low kinetic energy displacement bias in the transport map of the network, and link this bias with generalization performance. From this observation, we reformulate the learning problem as follows: finding neural networks which solve the task while transporting the data as efficiently as possible. This offers a novel formulation of the learning problem which allows us to provide regularity results for the solution network, based on Optimal Transport theory. From a practical viewpoint, this allows us to propose a new learning algorithm, which automatically adapts to the complexity of the given task, and leads to networks with a high generalization ability even in low data regimes.