Gradient-Informed Quality Diversity for the Illumination of Discrete Spaces

Quality Diversity (QD) algorithms have been proposed to search for a large collection of both diverse and high-performing solutions instead of a single set of local optima. While early QD algorithms view the objective and descriptor functions as black-box functions, novel tools have been introduced to use gradient information to accelerate the search and improve overall performance of those algorithms over continuous input spaces. However a broad range of applications involve discrete spaces, such as drug discovery or image generation. Exploring those spaces is challenging as they are combinatorially large and gradients cannot be used in the same manner as in continuous spaces. We introduce map-elites with a Gradient-Informed Discrete Emitter (ME-GIDE), which extends QD optimisation with differentiable functions over discrete search spaces. ME-GIDE leverages the gradient information of the objective and descriptor functions with respect to its discrete inputs to propose gradient-informed updates that guide the search towards a diverse set of high quality solutions. We evaluate our method on challenging benchmarks including protein design and discrete latent space illumination and find that our method outperforms state-of-the-art QD algorithms in all benchmarks.

Differentiable Feature Selection, a Reparameterization Approach

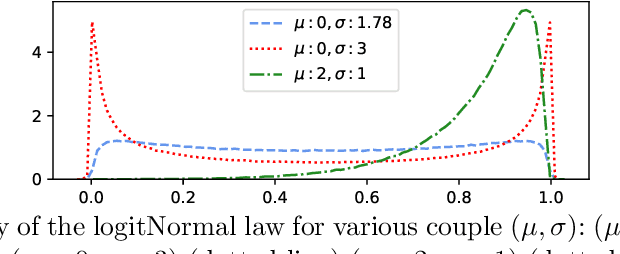
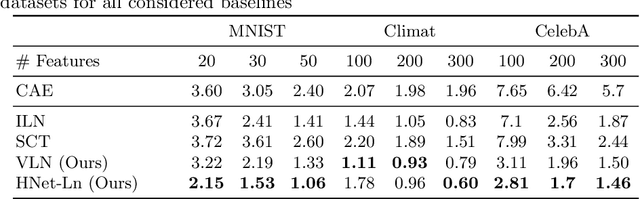
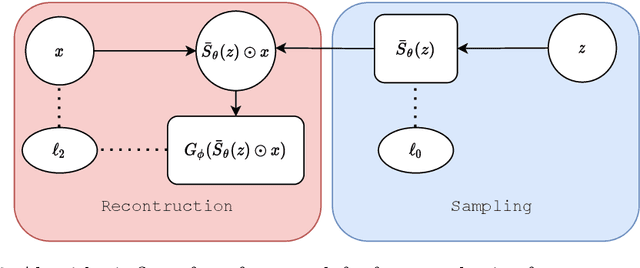
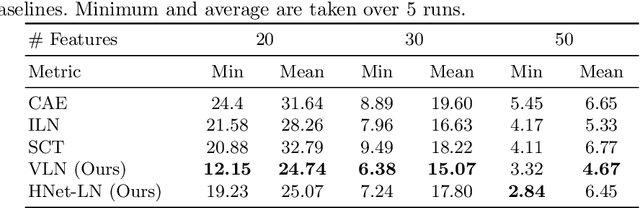
We consider the task of feature selection for reconstruction which consists in choosing a small subset of features from which whole data instances can be reconstructed. This is of particular importance in several contexts involving for example costly physical measurements, sensor placement or information compression. To break the intrinsic combinatorial nature of this problem, we formulate the task as optimizing a binary mask distribution enabling an accurate reconstruction. We then face two main challenges. One concerns differentiability issues due to the binary distribution. The second one corresponds to the elimination of redundant information by selecting variables in a correlated fashion which requires modeling the covariance of the binary distribution. We address both issues by introducing a relaxation of the problem via a novel reparameterization of the logitNormal distribution. We demonstrate that the proposed method provides an effective exploration scheme and leads to efficient feature selection for reconstruction through evaluation on several high dimensional image benchmarks. We show that the method leverages the intrinsic geometry of the data, facilitating reconstruction.

Augmenting Physical Models with Deep Networks for Complex Dynamics Forecasting

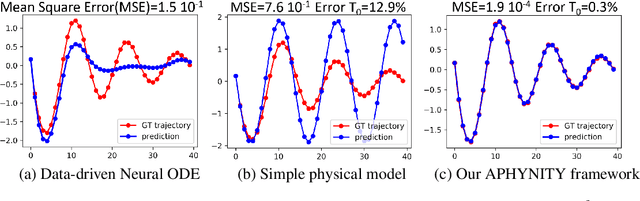
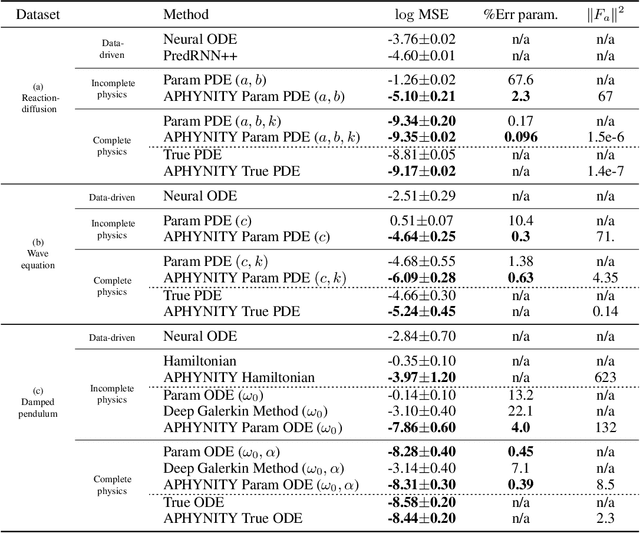
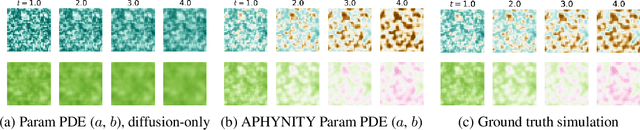
Forecasting complex dynamical phenomena in settings where only partial knowledge of their dynamics is available is a prevalent problem across various scientific fields. While purely data-driven approaches are arguably insufficient in this context, standard physical modeling based approaches tend to be over-simplistic, inducing non-negligible errors. In this work, we introduce the APHYNITY framework, a principled approach for augmenting incomplete physical dynamics described by differential equations with deep data-driven models. It consists in decomposing the dynamics into two components: a physical component accounting for the dynamics for which we have some prior knowledge, and a data-driven component accounting for errors of the physical model. The learning problem is carefully formulated such that the physical model explains as much of the data as possible, while the data-driven component only describes information that cannot be captured by the physical model, no more, no less. This not only provides the existence and uniqueness for this decomposition, but also ensures interpretability and benefits generalization. Experiments made on three important use cases, each representative of a different family of phenomena, i.e. reaction-diffusion equations, wave equations and the non-linear damped pendulum, show that APHYNITY can efficiently leverage approximate physical models to accurately forecast the evolution of the system and correctly identify relevant physical parameters.