Differentiable Feature Selection, a Reparameterization Approach
Paper and Code
Jul 21, 2021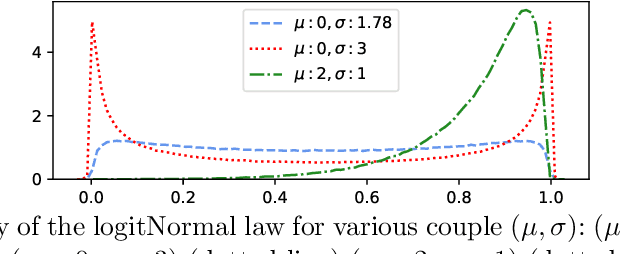
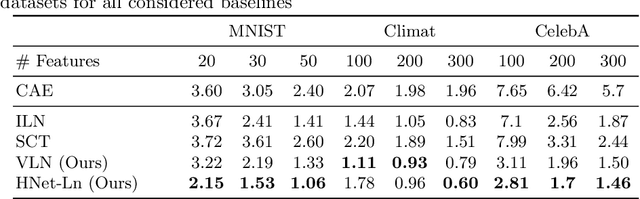
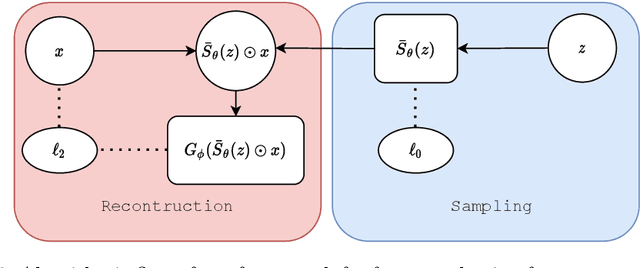
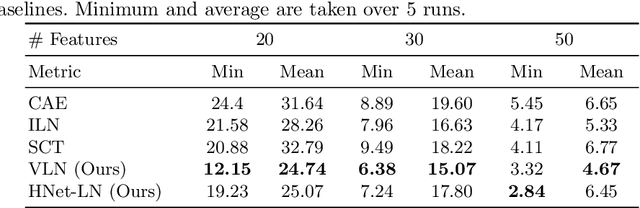
We consider the task of feature selection for reconstruction which consists in choosing a small subset of features from which whole data instances can be reconstructed. This is of particular importance in several contexts involving for example costly physical measurements, sensor placement or information compression. To break the intrinsic combinatorial nature of this problem, we formulate the task as optimizing a binary mask distribution enabling an accurate reconstruction. We then face two main challenges. One concerns differentiability issues due to the binary distribution. The second one corresponds to the elimination of redundant information by selecting variables in a correlated fashion which requires modeling the covariance of the binary distribution. We address both issues by introducing a relaxation of the problem via a novel reparameterization of the logitNormal distribution. We demonstrate that the proposed method provides an effective exploration scheme and leads to efficient feature selection for reconstruction through evaluation on several high dimensional image benchmarks. We show that the method leverages the intrinsic geometry of the data, facilitating reconstruction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge