Complementing Brightness Constancy with Deep Networks for Optical Flow Prediction

State-of-the-art methods for optical flow estimation rely on deep learning, which require complex sequential training schemes to reach optimal performances on real-world data. In this work, we introduce the COMBO deep network that explicitly exploits the brightness constancy (BC) model used in traditional methods. Since BC is an approximate physical model violated in several situations, we propose to train a physically-constrained network complemented with a data-driven network. We introduce a unique and meaningful flow decomposition between the physical prior and the data-driven complement, including an uncertainty quantification of the BC model. We derive a joint training scheme for learning the different components of the decomposition ensuring an optimal cooperation, in a supervised but also in a semi-supervised context. Experiments show that COMBO can improve performances over state-of-the-art supervised networks, e.g. RAFT, reaching state-of-the-art results on several benchmarks. We highlight how COMBO can leverage the BC model and adapt to its limitations. Finally, we show that our semi-supervised method can significantly simplify the training procedure.

Deep learning for spatio-temporal forecasting -- application to solar energy

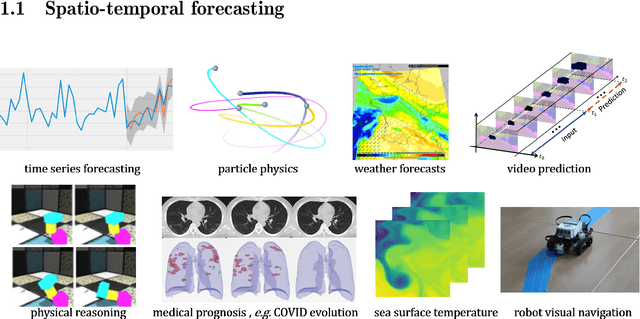
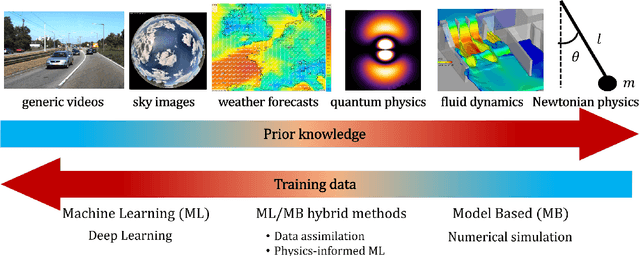
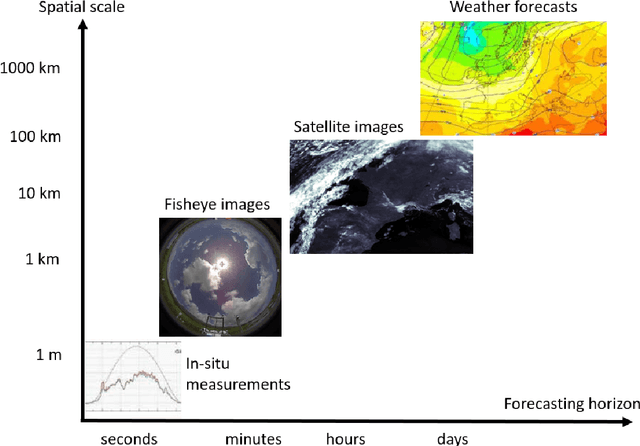
This thesis tackles the subject of spatio-temporal forecasting with deep learning. The motivating application at Electricity de France (EDF) is short-term solar energy forecasting with fisheye images. We explore two main research directions for improving deep forecasting methods by injecting external physical knowledge. The first direction concerns the role of the training loss function. We show that differentiable shape and temporal criteria can be leveraged to improve the performances of existing models. We address both the deterministic context with the proposed DILATE loss function and the probabilistic context with the STRIPE model. Our second direction is to augment incomplete physical models with deep data-driven networks for accurate forecasting. For video prediction, we introduce the PhyDNet model that disentangles physical dynamics from residual information necessary for prediction, such as texture or details. We further propose a learning framework (APHYNITY) that ensures a principled and unique linear decomposition between physical and data-driven components under mild assumptions, leading to better forecasting performances and parameter identification.

Deep Time Series Forecasting with Shape and Temporal Criteria

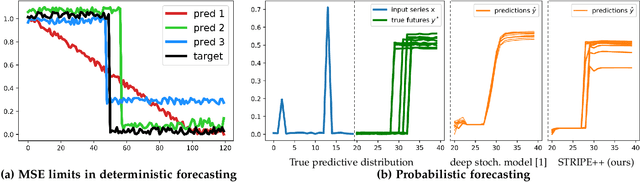
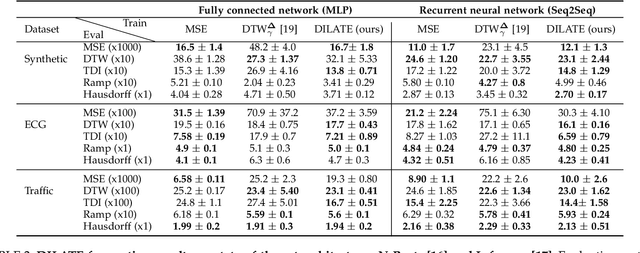
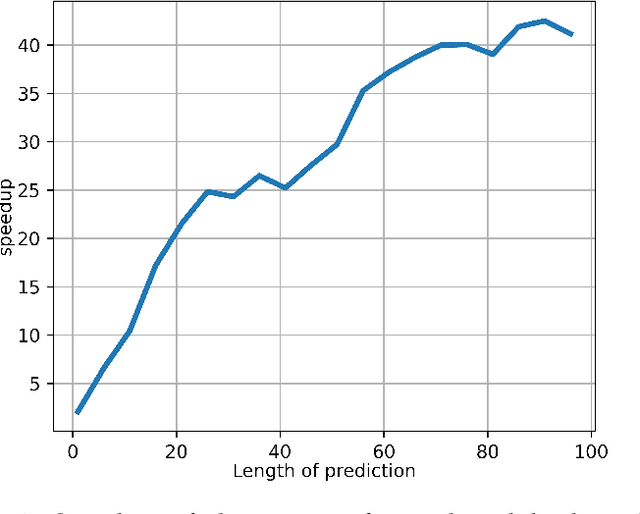
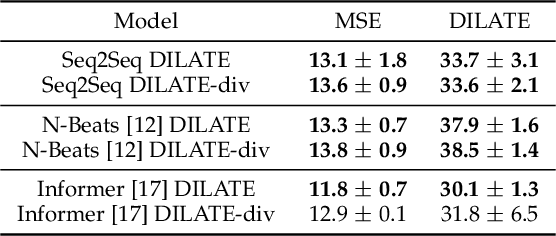
This paper addresses the problem of multi-step time series forecasting for non-stationary signals that can present sudden changes. Current state-of-the-art deep learning forecasting methods, often trained with variants of the MSE, lack the ability to provide sharp predictions in deterministic and probabilistic contexts. To handle these challenges, we propose to incorporate shape and temporal criteria in the training objective of deep models. We define shape and temporal similarities and dissimilarities, based on a smooth relaxation of Dynamic Time Warping (DTW) and Temporal Distortion Index (TDI), that enable to build differentiable loss functions and positive semi-definite (PSD) kernels. With these tools, we introduce DILATE (DIstortion Loss including shApe and TimE), a new objective for deterministic forecasting, that explicitly incorporates two terms supporting precise shape and temporal change detection. For probabilistic forecasting, we introduce STRIPE++ (Shape and Time diverRsIty in Probabilistic forEcasting), a framework for providing a set of sharp and diverse forecasts, where the structured shape and time diversity is enforced with a determinantal point process (DPP) diversity loss. Extensive experiments and ablations studies on synthetic and real-world datasets confirm the benefits of leveraging shape and time features in time series forecasting.

Probabilistic Time Series Forecasting with Structured Shape and Temporal Diversity

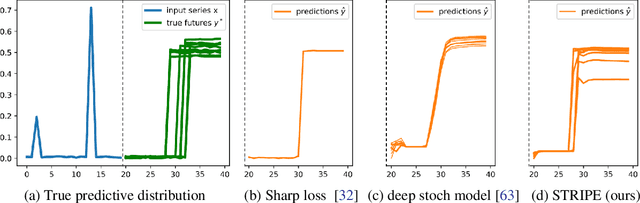
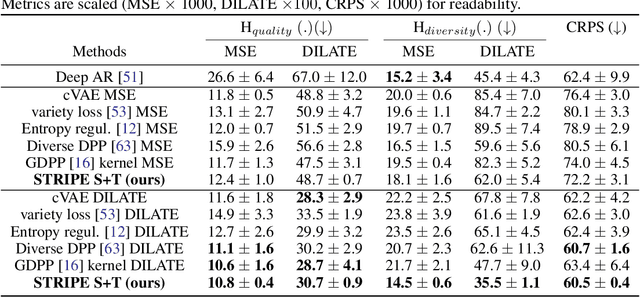
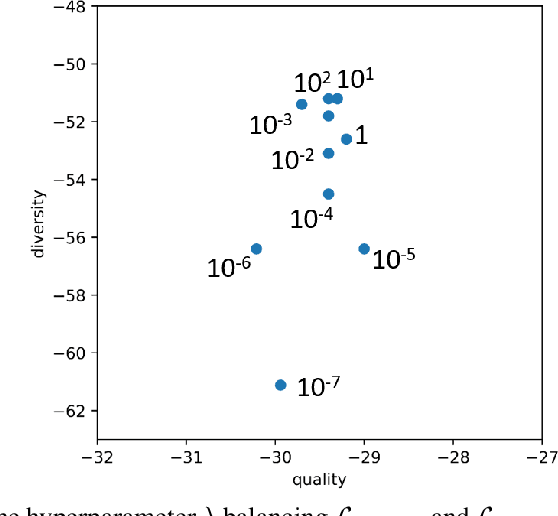
Probabilistic forecasting consists in predicting a distribution of possible future outcomes. In this paper, we address this problem for non-stationary time series, which is very challenging yet crucially important. We introduce the STRIPE model for representing structured diversity based on shape and time features, ensuring both probable predictions while being sharp and accurate. STRIPE is agnostic to the forecasting model, and we equip it with a diversification mechanism relying on determinantal point processes (DPP). We introduce two DPP kernels for modeling diverse trajectories in terms of shape and time, which are both differentiable and proved to be positive semi-definite. To have an explicit control on the diversity structure, we also design an iterative sampling mechanism to disentangle shape and time representations in the latent space. Experiments carried out on synthetic datasets show that STRIPE significantly outperforms baseline methods for representing diversity, while maintaining accuracy of the forecasting model. We also highlight the relevance of the iterative sampling scheme and the importance to use different criteria for measuring quality and diversity. Finally, experiments on real datasets illustrate that STRIPE is able to outperform state-of-the-art probabilistic forecasting approaches in the best sample prediction.

Augmenting Physical Models with Deep Networks for Complex Dynamics Forecasting

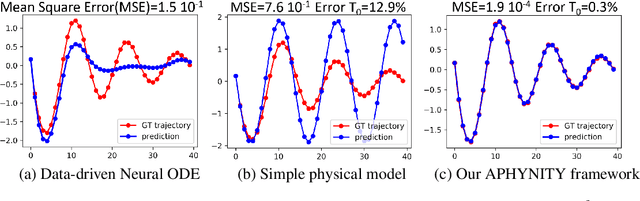
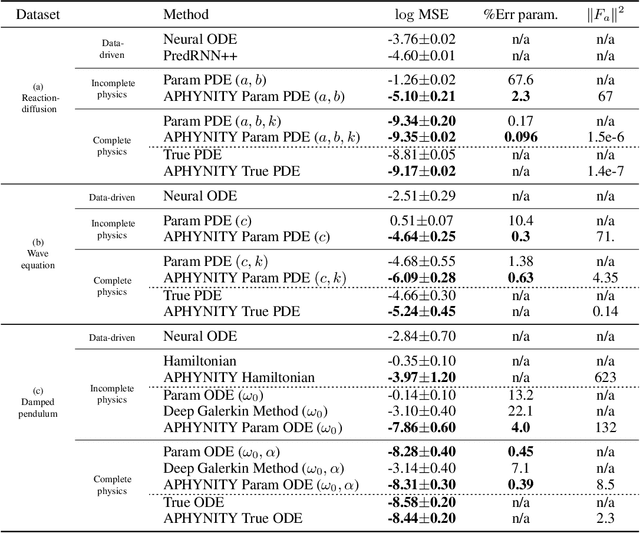
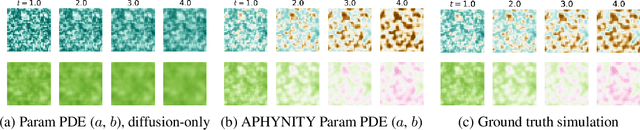
Forecasting complex dynamical phenomena in settings where only partial knowledge of their dynamics is available is a prevalent problem across various scientific fields. While purely data-driven approaches are arguably insufficient in this context, standard physical modeling based approaches tend to be over-simplistic, inducing non-negligible errors. In this work, we introduce the APHYNITY framework, a principled approach for augmenting incomplete physical dynamics described by differential equations with deep data-driven models. It consists in decomposing the dynamics into two components: a physical component accounting for the dynamics for which we have some prior knowledge, and a data-driven component accounting for errors of the physical model. The learning problem is carefully formulated such that the physical model explains as much of the data as possible, while the data-driven component only describes information that cannot be captured by the physical model, no more, no less. This not only provides the existence and uniqueness for this decomposition, but also ensures interpretability and benefits generalization. Experiments made on three important use cases, each representative of a different family of phenomena, i.e. reaction-diffusion equations, wave equations and the non-linear damped pendulum, show that APHYNITY can efficiently leverage approximate physical models to accurately forecast the evolution of the system and correctly identify relevant physical parameters.

Disentangling Physical Dynamics from Unknown Factors for Unsupervised Video Prediction

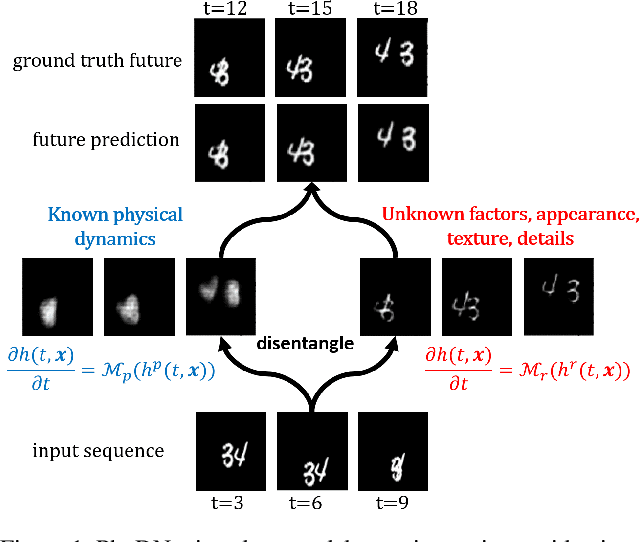
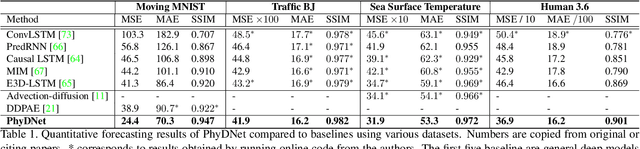
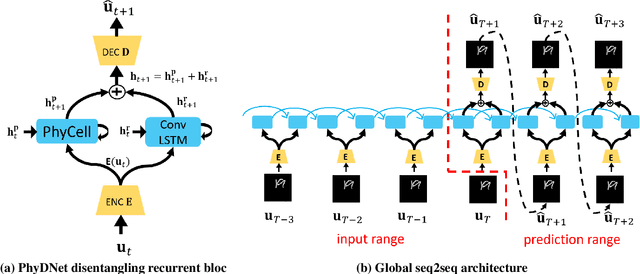
Leveraging physical knowledge described by partial differential equations (PDEs) is an appealing way to improve unsupervised video prediction methods. Since physics is too restrictive for describing the full visual content of generic videos, we introduce PhyDNet, a two-branch deep architecture, which explicitly disentangles PDE dynamics from unknown complementary information. A second contribution is to propose a new recurrent physical cell (PhyCell), inspired from data assimilation techniques, for performing PDE-constrained prediction in latent space. Extensive experiments conducted on four various datasets show the ability of PhyDNet to outperform state-of-the-art methods. Ablation studies also highlight the important gain brought out by both disentanglement and PDE-constrained prediction. Finally, we show that PhyDNet presents interesting features for dealing with missing data and long-term forecasting.

Shape and Time Distortion Loss for Training Deep Time Series Forecasting Models

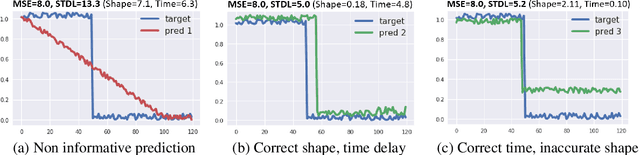
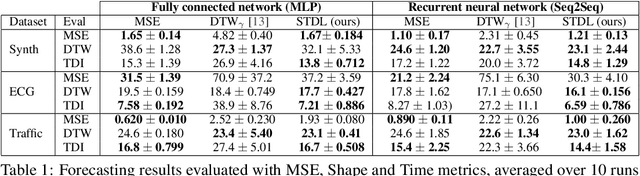
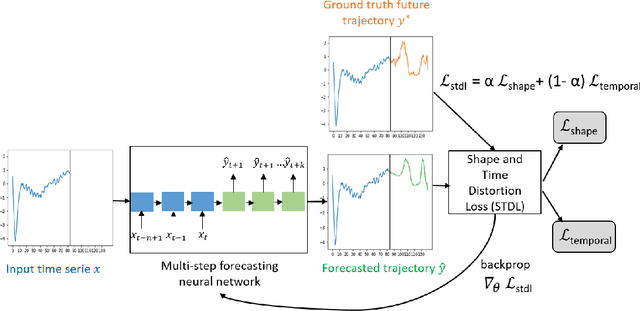
This paper addresses the problem of time series forecasting for non-stationary signals and multiple future steps prediction. To handle this challenging task, we introduce DILATE (DIstortion Loss including shApe and TimE), a new objective function for training deep neural networks. DILATE aims at accurately predicting sudden changes, and explicitly incorporates two terms supporting precise shape and temporal change detection. We introduce a differentiable loss function suitable for training deep neural nets, and provide a custom back-prop implementation for speeding up optimization. We also introduce a variant of DILATE, which provides a smooth generalization of temporally-constrained Dynamic Time Warping (DTW). Experiments carried out on various non-stationary datasets reveal the very good behaviour of DILATE compared to models trained with the standard Mean Squared Error (MSE) loss function, and also to DTW and variants. DILATE is also agnostic to the choice of the model, and we highlight its benefit for training fully connected networks as well as specialized recurrent architectures, showing its capacity to improve over state-of-the-art trajectory forecasting approaches.