Module-wise Training of Neural Networks via the Minimizing Movement Scheme

Greedy layer-wise or module-wise training of neural networks is compelling in constrained and on-device settings where memory is limited, as it circumvents a number of problems of end-to-end back-propagation. However, it suffers from a stagnation problem, whereby early layers overfit and deeper layers stop increasing the test accuracy after a certain depth. We propose to solve this issue by introducing a module-wise regularization inspired by the minimizing movement scheme for gradient flows in distribution space. We call the method TRGL for Transport Regularized Greedy Learning and study it theoretically, proving that it leads to greedy modules that are regular and that progressively solve the task. Experimentally, we show improved accuracy of module-wise training of various architectures such as ResNets, Transformers and VGG, when our regularization is added, superior to that of other module-wise training methods and often to end-to-end training, with as much as 60% less memory usage.

Module-wise Training of Residual Networks via the Minimizing Movement Scheme

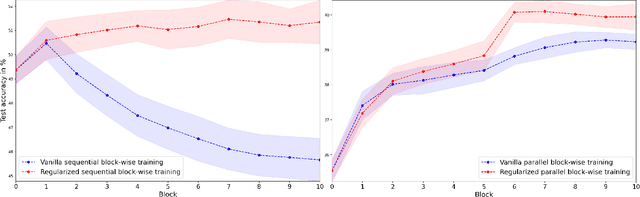
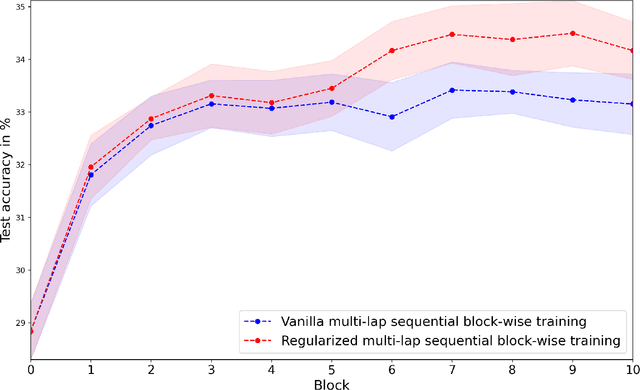
Greedy layer-wise or module-wise training of neural networks is compelling in constrained and on-device settings, as it circumvents a number of problems of end-to-end back-propagation. However, it suffers from a stagnation problem, whereby early layers overfit and deeper layers stop increasing the test accuracy after a certain depth. We propose to solve this issue by introducing a simple module-wise regularization inspired by the minimizing movement scheme for gradient flows in distribution space. The method, which we call TRGL for Transport Regularized Greedy Learning, is particularly well-adapted to residual networks. We study it theoretically, proving that it leads to greedy modules that are regular and that successively solve the task. Experimentally, we show improved accuracy of module-wise trained networks when our regularization is added.

A Neural Tangent Kernel Perspective of GANs

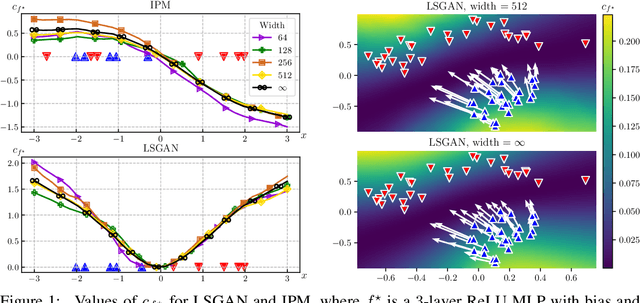
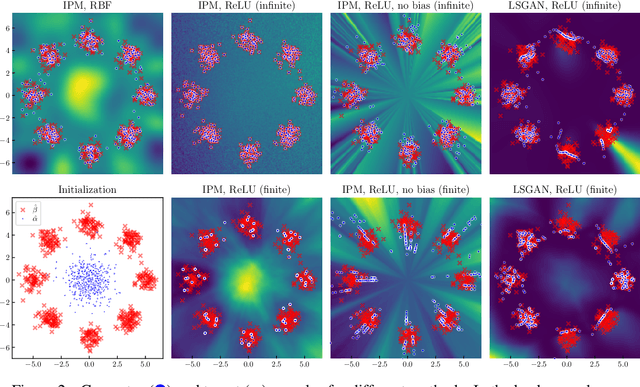
Theoretical analyses for Generative Adversarial Networks (GANs) generally assume an arbitrarily large family of discriminators and do not consider the characteristics of the architectures used in practice. We show that this framework of analysis is too simplistic to properly analyze GAN training. To tackle this issue, we leverage the theory of infinite-width neural networks to model neural discriminator training for a wide range of adversarial losses via its Neural Tangent Kernel (NTK). Our analytical results show that GAN trainability primarily depends on the discriminator's architecture. We further study the discriminator for specific architectures and losses, and highlight properties providing a new understanding of GAN training. For example, we find that GANs trained with the integral probability metric loss minimize the maximum mean discrepancy with the NTK as kernel. Our conclusions demonstrate the analysis opportunities provided by the proposed framework, which paves the way for better and more principled GAN models. We release a generic GAN analysis toolkit based on our framework that supports the empirical part of our study.

LEADS: Learning Dynamical Systems that Generalize Across Environments

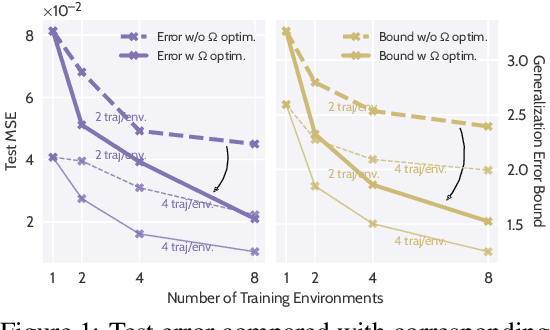
When modeling dynamical systems from real-world data samples, the distribution of data often changes according to the environment in which they are captured, and the dynamics of the system itself vary from one environment to another. Generalizing across environments thus challenges the conventional frameworks. The classical settings suggest either considering data as i.i.d. and learning a single model to cover all situations or learning environment-specific models. Both are sub-optimal: the former disregards the discrepancies between environments leading to biased solutions, while the latter does not exploit their potential commonalities and is prone to scarcity problems. We propose LEADS, a novel framework that leverages the commonalities and discrepancies among known environments to improve model generalization. This is achieved with a tailored training formulation aiming at capturing common dynamics within a shared model while additional terms capture environment-specific dynamics. We ground our approach in theory, exhibiting a decrease in sample complexity with our approach and corroborate these results empirically, instantiating it for linear dynamics. Moreover, we concretize this framework for neural networks and evaluate it experimentally on representative families of nonlinear dynamics. We show that this new setting can exploit knowledge extracted from environment-dependent data and improves generalization for both known and novel environments.

Augmenting Physical Models with Deep Networks for Complex Dynamics Forecasting

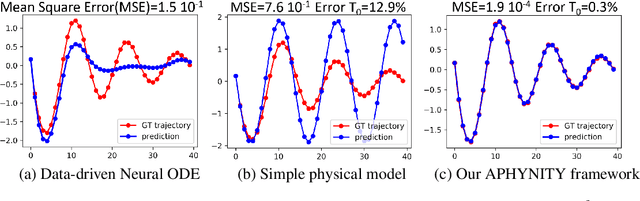
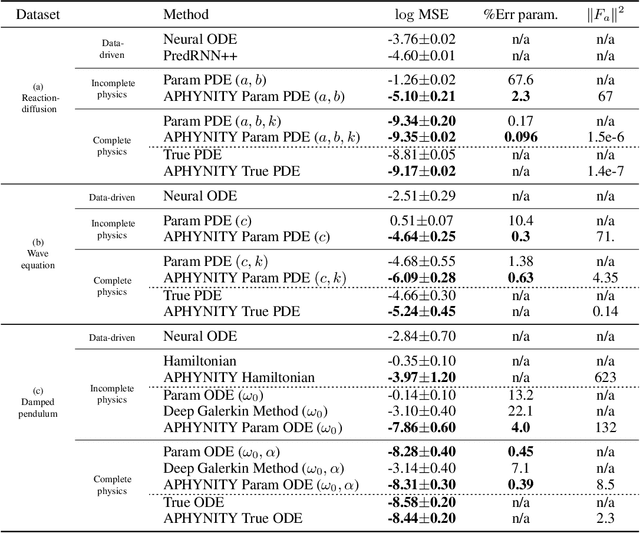
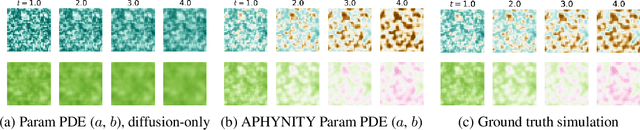
Forecasting complex dynamical phenomena in settings where only partial knowledge of their dynamics is available is a prevalent problem across various scientific fields. While purely data-driven approaches are arguably insufficient in this context, standard physical modeling based approaches tend to be over-simplistic, inducing non-negligible errors. In this work, we introduce the APHYNITY framework, a principled approach for augmenting incomplete physical dynamics described by differential equations with deep data-driven models. It consists in decomposing the dynamics into two components: a physical component accounting for the dynamics for which we have some prior knowledge, and a data-driven component accounting for errors of the physical model. The learning problem is carefully formulated such that the physical model explains as much of the data as possible, while the data-driven component only describes information that cannot be captured by the physical model, no more, no less. This not only provides the existence and uniqueness for this decomposition, but also ensures interpretability and benefits generalization. Experiments made on three important use cases, each representative of a different family of phenomena, i.e. reaction-diffusion equations, wave equations and the non-linear damped pendulum, show that APHYNITY can efficiently leverage approximate physical models to accurately forecast the evolution of the system and correctly identify relevant physical parameters.

Optimal Unsupervised Domain Translation

Domain Translation is the problem of finding a meaningful correspondence between two domains. Since in a majority of settings paired supervision is not available, much work focuses on Unsupervised Domain Translation (UDT) where data samples from each domain are unpaired. Following the seminal work of CycleGAN for UDT, many variants and extensions of this model have been proposed. However, there is still little theoretical understanding behind their success. We observe that these methods yield solutions which are approximately minimal w.r.t. a given transportation cost, leading us to reformulate the problem in the Optimal Transport (OT) framework. This viewpoint gives us a new perspective on Unsupervised Domain Translation and allows us to prove the existence and uniqueness of the retrieved mapping, given a large family of transport costs. We then propose a novel framework to efficiently compute optimal mappings in a dynamical setting. We show that it generalizes previous methods and enables a more explicit control over the computed optimal mapping. It also provides smooth interpolations between the two domains. Experiments on toy and real world datasets illustrate the behavior of our method.

Learning Dynamical Systems from Partial Observations

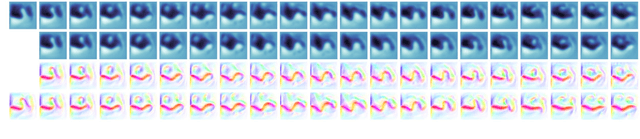
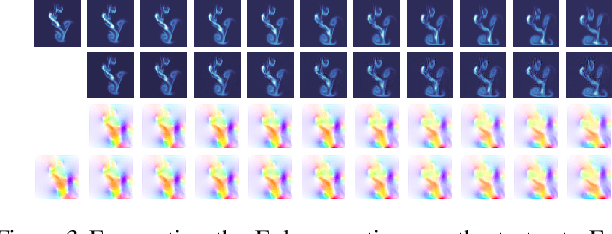
We consider the problem of forecasting complex, nonlinear space-time processes when observations provide only partial information of on the system's state. We propose a natural data-driven framework, where the system's dynamics are modelled by an unknown time-varying differential equation, and the evolution term is estimated from the data, using a neural network. Any future state can then be computed by placing the associated differential equation in an ODE solver. We first evaluate our approach on shallow water and Euler simulations. We find that our method not only demonstrates high quality long-term forecasts, but also learns to produce hidden states closely resembling the true states of the system, without direct supervision on the latter. Additional experiments conducted on challenging, state of the art ocean simulations further validate our findings, while exhibiting notable improvements over classical baselines.