Unsupervised Adversarial Image Inpainting

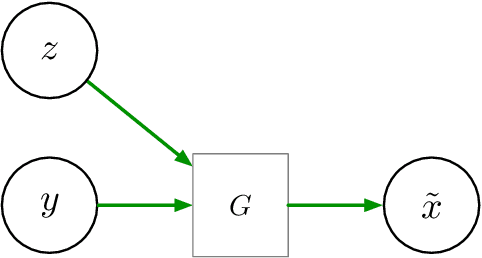
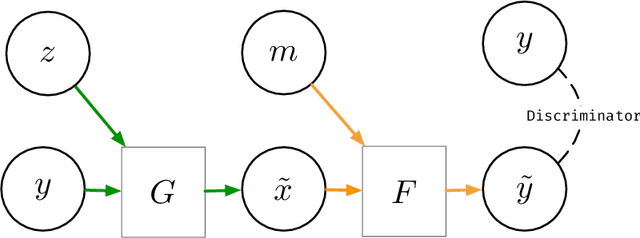
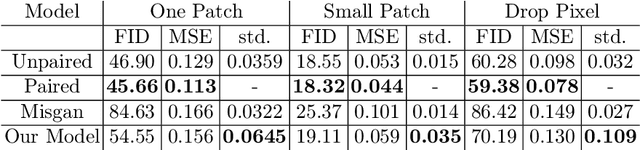
We consider inpainting in an unsupervised setting where there is neither access to paired nor unpaired training data. The only available information is provided by the uncomplete observations and the inpainting process statistics. In this context, an observation should give rise to several plausible reconstructions which amounts at learning a distribution over the space of reconstructed images. We model the reconstruction process by using a conditional GAN with constraints on the stochastic component that introduce an explicit dependency between this component and the generated output. This allows us sampling from the latent component in order to generate a distribution of images associated to an observation. We demonstrate the capacity of our model on several image datasets: faces (CelebA), food images (Recipe-1M) and bedrooms (LSUN Bedrooms) with different types of imputation masks. The approach yields comparable performance to model variants trained with additional supervision.

Learning Dynamical Systems from Partial Observations

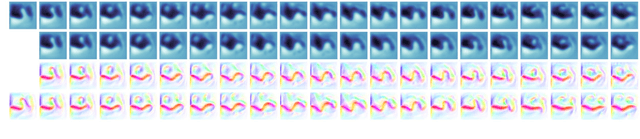
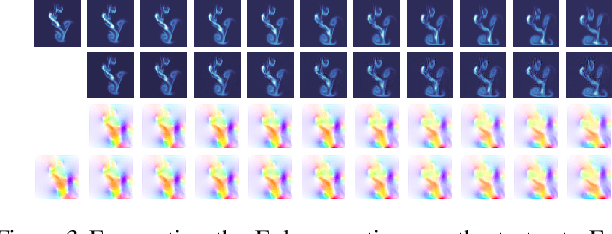
We consider the problem of forecasting complex, nonlinear space-time processes when observations provide only partial information of on the system's state. We propose a natural data-driven framework, where the system's dynamics are modelled by an unknown time-varying differential equation, and the evolution term is estimated from the data, using a neural network. Any future state can then be computed by placing the associated differential equation in an ODE solver. We first evaluate our approach on shallow water and Euler simulations. We find that our method not only demonstrates high quality long-term forecasts, but also learns to produce hidden states closely resembling the true states of the system, without direct supervision on the latter. Additional experiments conducted on challenging, state of the art ocean simulations further validate our findings, while exhibiting notable improvements over classical baselines.

Deep Learning for Physical Processes: Incorporating Prior Scientific Knowledge

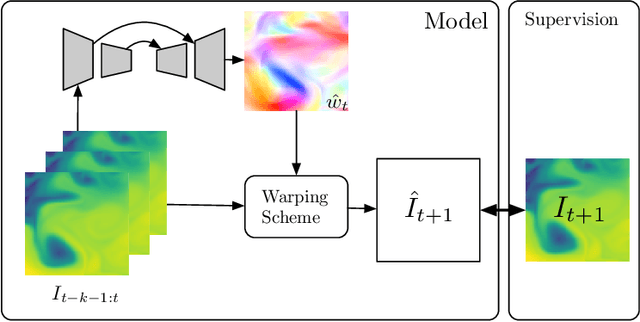
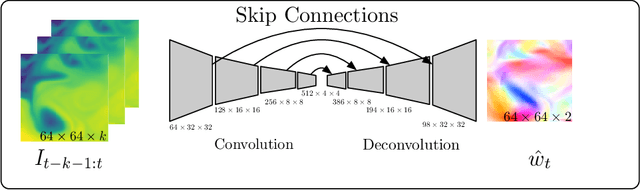
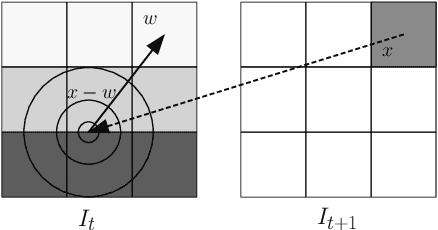
We consider the use of Deep Learning methods for modeling complex phenomena like those occurring in natural physical processes. With the large amount of data gathered on these phenomena the data intensive paradigm could begin to challenge more traditional approaches elaborated over the years in fields like maths or physics. However, despite considerable successes in a variety of application domains, the machine learning field is not yet ready to handle the level of complexity required by such problems. Using an example application, namely Sea Surface Temperature Prediction, we show how general background knowledge gained from physics could be used as a guideline for designing efficient Deep Learning models. In order to motivate the approach and to assess its generality we demonstrate a formal link between the solution of a class of differential equations underlying a large family of physical phenomena and the proposed model. Experiments and comparison with series of baselines including a state of the art numerical approach is then provided.