Learning a Neural Solver for Parametric PDE to Enhance Physics-Informed Methods

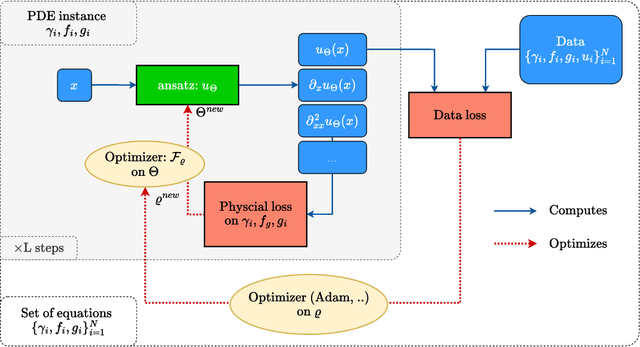
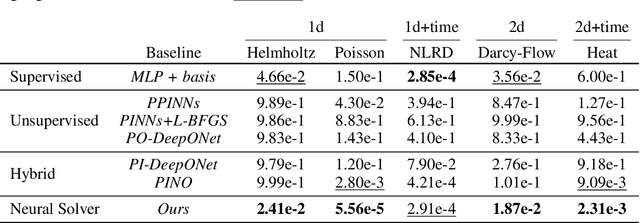
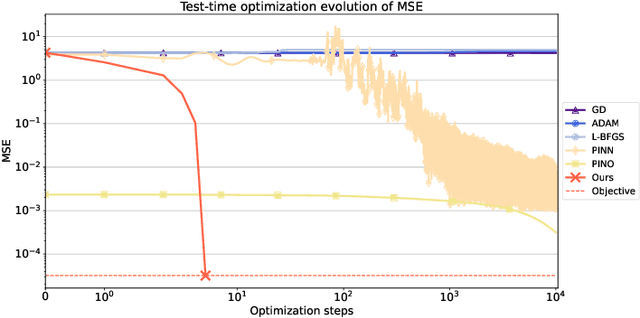
Physics-informed deep learning often faces optimization challenges due to the complexity of solving partial differential equations (PDEs), which involve exploring large solution spaces, require numerous iterations, and can lead to unstable training. These challenges arise particularly from the ill-conditioning of the optimization problem, caused by the differential terms in the loss function. To address these issues, we propose learning a solver, i.e., solving PDEs using a physics-informed iterative algorithm trained on data. Our method learns to condition a gradient descent algorithm that automatically adapts to each PDE instance, significantly accelerating and stabilizing the optimization process and enabling faster convergence of physics-aware models. Furthermore, while traditional physics-informed methods solve for a single PDE instance, our approach addresses parametric PDEs. Specifically, our method integrates the physical loss gradient with the PDE parameters to solve over a distribution of PDE parameters, including coefficients, initial conditions, or boundary conditions. We demonstrate the effectiveness of our method through empirical experiments on multiple datasets, comparing training and test-time optimization performance.

Convolutional Neural Operators

Although very successfully used in machine learning, convolution based neural network architectures -- believed to be inconsistent in function space -- have been largely ignored in the context of learning solution operators of PDEs. Here, we adapt convolutional neural networks to demonstrate that they are indeed able to process functions as inputs and outputs. The resulting architecture, termed as convolutional neural operators (CNOs), is shown to significantly outperform competing models on benchmark experiments, paving the way for the design of an alternative robust and accurate framework for learning operators.

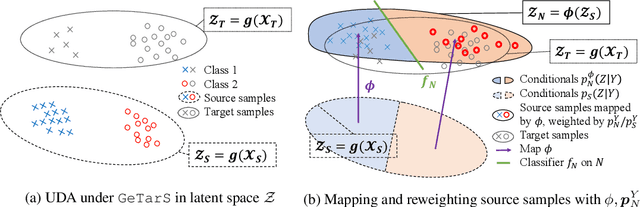
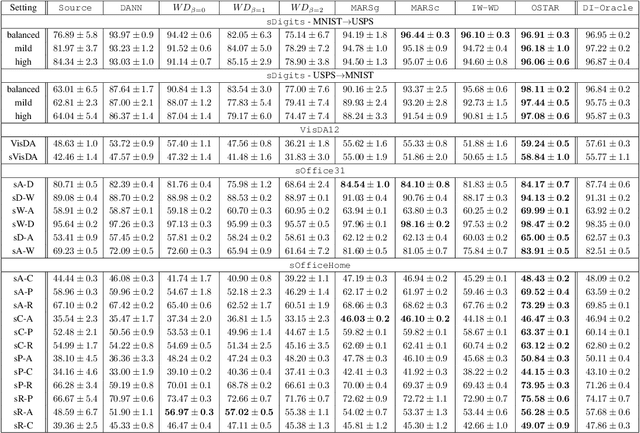
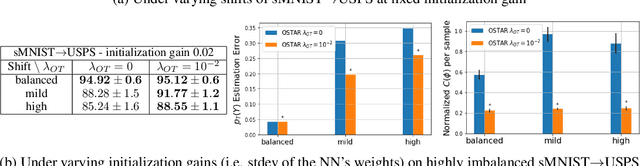
Mapping conditional distributions for domain adaptation under generalized target shift

We consider the problem of unsupervised domain adaptation (UDA) between a source and a target domain under conditional and label shift a.k.a Generalized Target Shift (GeTarS). Unlike simpler UDA settings, few works have addressed this challenging problem. Recent approaches learn domain-invariant representations, yet they have practical limitations and rely on strong assumptions that may not hold in practice. In this paper, we explore a novel and general approach to align pretrained representations, which circumvents existing drawbacks. Instead of constraining representation invariance, it learns an optimal transport map, implemented as a NN, which maps source representations onto target ones. Our approach is flexible and scalable, it preserves the problem's structure and it has strong theoretical guarantees under mild assumptions. In particular, our solution is unique, matches conditional distributions across domains, recovers target proportions and explicitly controls the target generalization risk. Through an exhaustive comparison on several datasets, we challenge the state-of-the-art in GeTarS.

Unsupervised Adversarial Image Inpainting

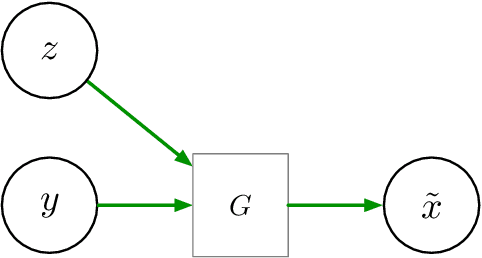
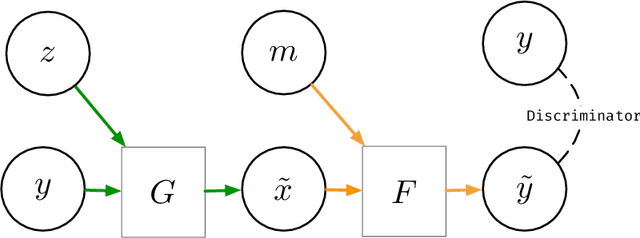
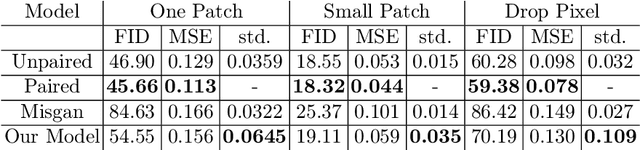
We consider inpainting in an unsupervised setting where there is neither access to paired nor unpaired training data. The only available information is provided by the uncomplete observations and the inpainting process statistics. In this context, an observation should give rise to several plausible reconstructions which amounts at learning a distribution over the space of reconstructed images. We model the reconstruction process by using a conditional GAN with constraints on the stochastic component that introduce an explicit dependency between this component and the generated output. This allows us sampling from the latent component in order to generate a distribution of images associated to an observation. We demonstrate the capacity of our model on several image datasets: faces (CelebA), food images (Recipe-1M) and bedrooms (LSUN Bedrooms) with different types of imputation masks. The approach yields comparable performance to model variants trained with additional supervision.

Deep Learning for Physical Processes: Incorporating Prior Scientific Knowledge

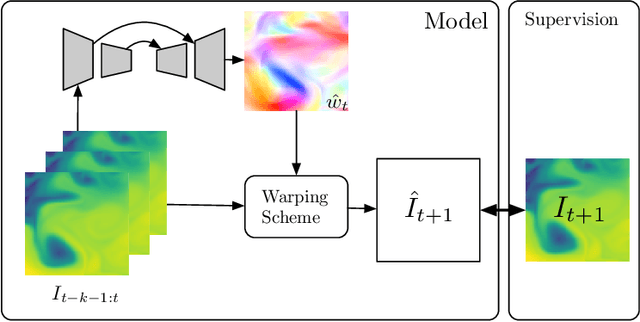
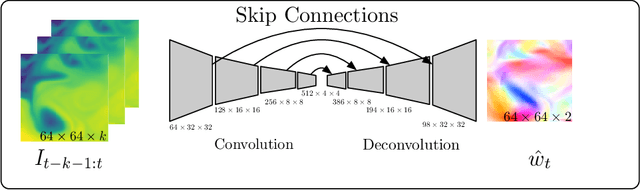
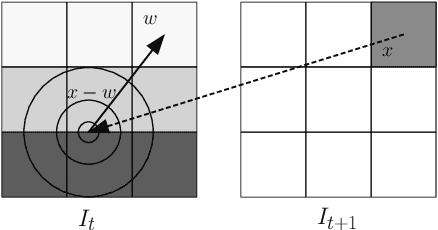
We consider the use of Deep Learning methods for modeling complex phenomena like those occurring in natural physical processes. With the large amount of data gathered on these phenomena the data intensive paradigm could begin to challenge more traditional approaches elaborated over the years in fields like maths or physics. However, despite considerable successes in a variety of application domains, the machine learning field is not yet ready to handle the level of complexity required by such problems. Using an example application, namely Sea Surface Temperature Prediction, we show how general background knowledge gained from physics could be used as a guideline for designing efficient Deep Learning models. In order to motivate the approach and to assess its generality we demonstrate a formal link between the solution of a class of differential equations underlying a large family of physical phenomena and the proposed model. Experiments and comparison with series of baselines including a state of the art numerical approach is then provided.