Computing Wasserstein Barycenters through Gradient Flows

Wasserstein barycenters provide a powerful tool for aggregating probability measures, while leveraging the geometry of their ambient space. Existing discrete methods suffer from poor scalability, as they require access to the complete set of samples from input measures. We address this issue by recasting the original barycenter problem as a gradient flow in the Wasserstein space. Our approach offers two advantages. First, we achieve scalability by sampling mini-batches from the input measures. Second, we incorporate functionals over probability measures, which regularize the barycenter problem through internal, potential, and interaction energies. We present two algorithms for empirical and Gaussian mixture measures, providing convergence guarantees under the Polyak-{\L}ojasiewicz inequality. Experimental validation on toy datasets and domain adaptation benchmarks show that our methods outperform previous discrete and neural net-based methods for computing Wasserstein barycenters.

Differentially Private Gradient Flow based on the Sliced Wasserstein Distance for Non-Parametric Generative Modeling

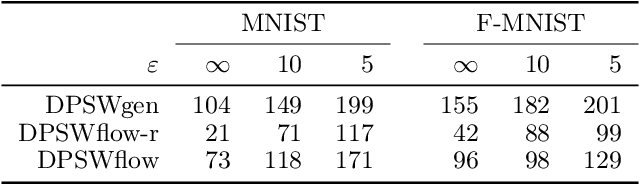
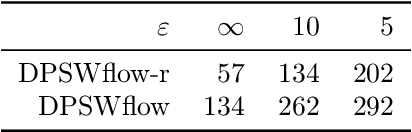
Safeguarding privacy in sensitive training data is paramount, particularly in the context of generative modeling. This is done through either differentially private stochastic gradient descent, or with a differentially private metric for training models or generators. In this paper, we introduce a novel differentially private generative modeling approach based on parameter-free gradient flows in the space of probability measures. The proposed algorithm is a new discretized flow which operates through a particle scheme, utilizing drift derived from the sliced Wasserstein distance and computed in a private manner. Our experiments show that compared to a generator-based model, our proposed model can generate higher-fidelity data at a low privacy budget, offering a viable alternative to generator-based approaches.

Unifying GANs and Score-Based Diffusion as Generative Particle Models

Particle-based deep generative models, such as gradient flows and score-based diffusion models, have recently gained traction thanks to their striking performance. Their principle of displacing particle distributions by differential equations is conventionally seen as opposed to the previously widespread generative adversarial networks (GANs), which involve training a pushforward generator network. In this paper, we challenge this interpretation and propose a novel framework that unifies particle and adversarial generative models by framing generator training as a generalization of particle models. This suggests that a generator is an optional addition to any such generative model. Consequently, integrating a generator into a score-based diffusion model and training a GAN without a generator naturally emerge from our framework. We empirically test the viability of these original models as proofs of concepts of potential applications of our framework.

Learning from Multiple Sources for Data-to-Text and Text-to-Data

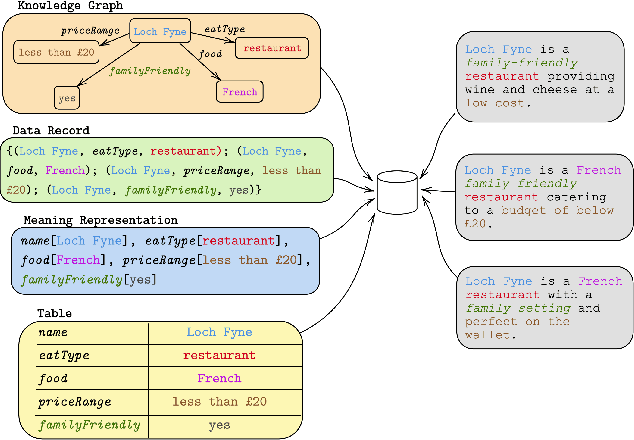
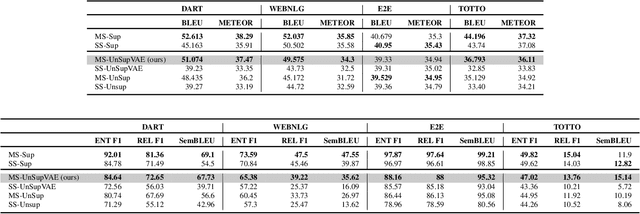
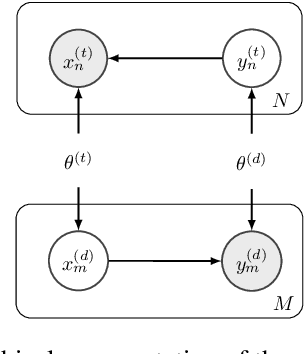
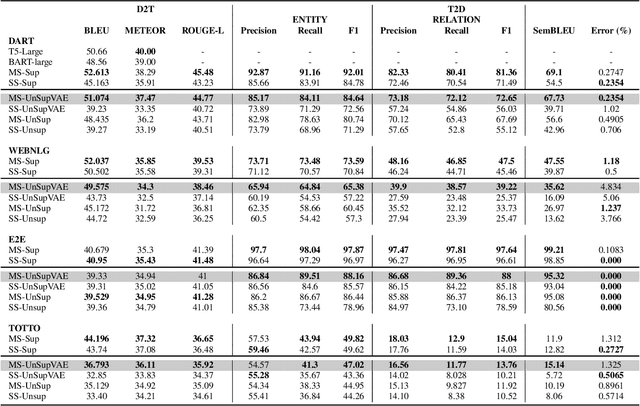
Data-to-text (D2T) and text-to-data (T2D) are dual tasks that convert structured data, such as graphs or tables into fluent text, and vice versa. These tasks are usually handled separately and use corpora extracted from a single source. Current systems leverage pre-trained language models fine-tuned on D2T or T2D tasks. This approach has two main limitations: first, a separate system has to be tuned for each task and source; second, learning is limited by the scarcity of available corpora. This paper considers a more general scenario where data are available from multiple heterogeneous sources. Each source, with its specific data format and semantic domain, provides a non-parallel corpus of text and structured data. We introduce a variational auto-encoder model with disentangled style and content variables that allows us to represent the diversity that stems from multiple sources of text and data. Our model is designed to handle the tasks of D2T and T2D jointly. We evaluate our model on several datasets, and show that by learning from multiple sources, our model closes the performance gap with its supervised single-source counterpart and outperforms it in some cases.

Scalable MCMC Sampling for Nonsymmetric Determinantal Point Processes

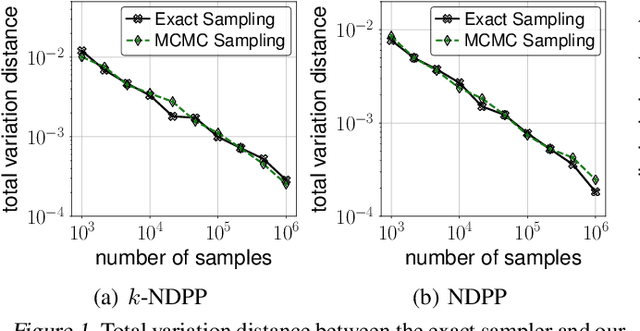
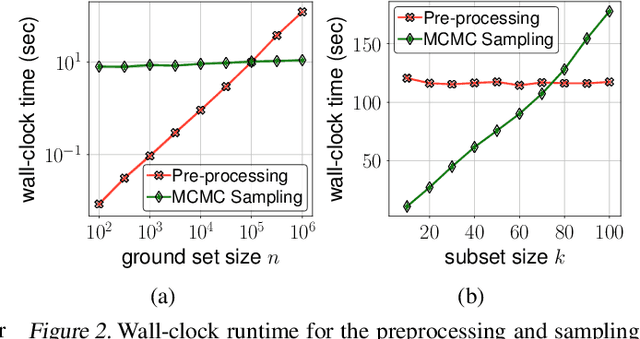
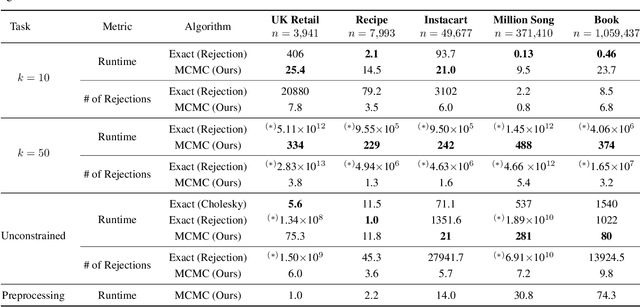
A determinantal point process (DPP) is an elegant model that assigns a probability to every subset of a collection of $n$ items. While conventionally a DPP is parameterized by a symmetric kernel matrix, removing this symmetry constraint, resulting in nonsymmetric DPPs (NDPPs), leads to significant improvements in modeling power and predictive performance. Recent work has studied an approximate Markov chain Monte Carlo (MCMC) sampling algorithm for NDPPs restricted to size-$k$ subsets (called $k$-NDPPs). However, the runtime of this approach is quadratic in $n$, making it infeasible for large-scale settings. In this work, we develop a scalable MCMC sampling algorithm for $k$-NDPPs with low-rank kernels, thus enabling runtime that is sublinear in $n$. Our method is based on a state-of-the-art NDPP rejection sampling algorithm, which we enhance with a novel approach for efficiently constructing the proposal distribution. Furthermore, we extend our scalable $k$-NDPP sampling algorithm to NDPPs without size constraints. Our resulting sampling method has polynomial time complexity in the rank of the kernel, while the existing approach has runtime that is exponential in the rank. With both a theoretical analysis and experiments on real-world datasets, we verify that our scalable approximate sampling algorithms are orders of magnitude faster than existing sampling approaches for $k$-NDPPs and NDPPs.

Scalable Sampling for Nonsymmetric Determinantal Point Processes

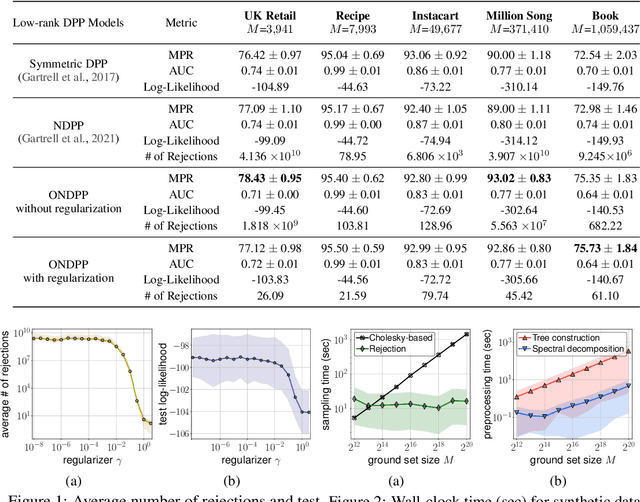
A determinantal point process (DPP) on a collection of $M$ items is a model, parameterized by a symmetric kernel matrix, that assigns a probability to every subset of those items. Recent work shows that removing the kernel symmetry constraint, yielding nonsymmetric DPPs (NDPPs), can lead to significant predictive performance gains for machine learning applications. However, existing work leaves open the question of scalable NDPP sampling. There is only one known DPP sampling algorithm, based on Cholesky decomposition, that can directly apply to NDPPs as well. Unfortunately, its runtime is cubic in $M$, and thus does not scale to large item collections. In this work, we first note that this algorithm can be transformed into a linear-time one for kernels with low-rank structure. Furthermore, we develop a scalable sublinear-time rejection sampling algorithm by constructing a novel proposal distribution. Additionally, we show that imposing certain structural constraints on the NDPP kernel enables us to bound the rejection rate in a way that depends only on the kernel rank. In our experiments we compare the speed of all of these samplers for a variety of real-world tasks.

Combining Reward and Rank Signals for Slate Recommendation

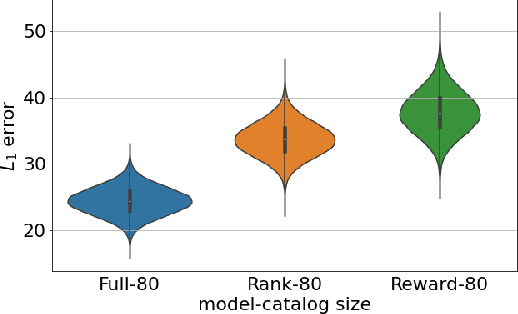
We consider the problem of slate recommendation, where the recommender system presents a user with a collection or slate composed of K recommended items at once. If the user finds the recommended items appealing then the user may click and the recommender system receives some feedback. Two pieces of information are available to the recommender system: was the slate clicked? (the reward), and if the slate was clicked, which item was clicked? (rank). In this paper, we formulate several Bayesian models that incorporate the reward signal (Reward model), the rank signal (Rank model), or both (Full model), for non-personalized slate recommendation. In our experiments, we analyze performance gains of the Full model and show that it achieves significantly lower error as the number of products in the catalog grows or as the slate size increases.

Wasserstein Learning of Determinantal Point Processes

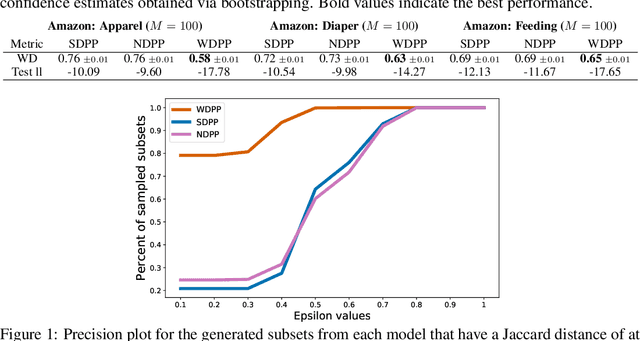
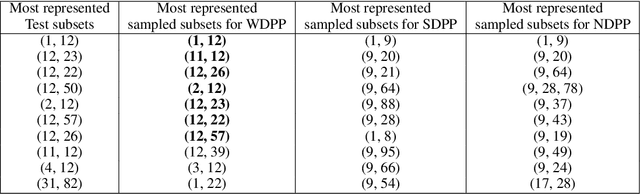
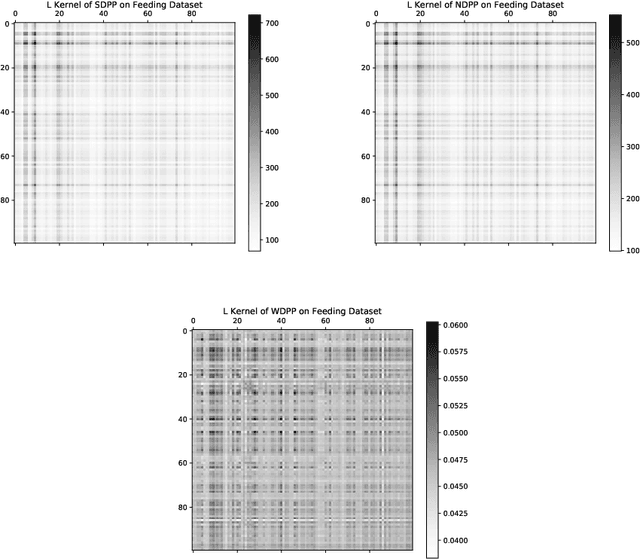
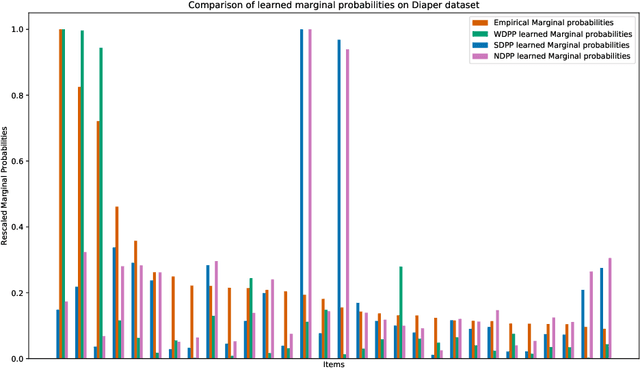
Determinantal point processes (DPPs) have received significant attention as an elegant probabilistic model for discrete subset selection. Most prior work on DPP learning focuses on maximum likelihood estimation (MLE). While efficient and scalable, MLE approaches do not leverage any subset similarity information and may fail to recover the true generative distribution of discrete data. In this work, by deriving a differentiable relaxation of a DPP sampling algorithm, we present a novel approach for learning DPPs that minimizes the Wasserstein distance between the model and data composed of observed subsets. Through an evaluation on a real-world dataset, we show that our Wasserstein learning approach provides significantly improved predictive performance on a generative task compared to DPPs trained using MLE.

Scalable Learning and MAP Inference for Nonsymmetric Determinantal Point Processes

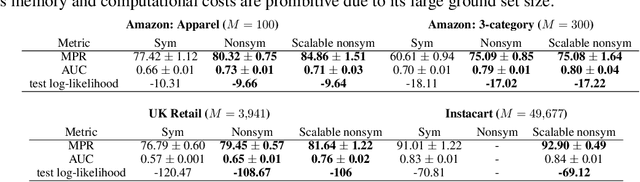
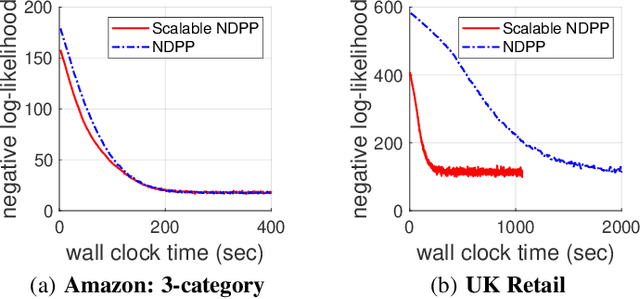
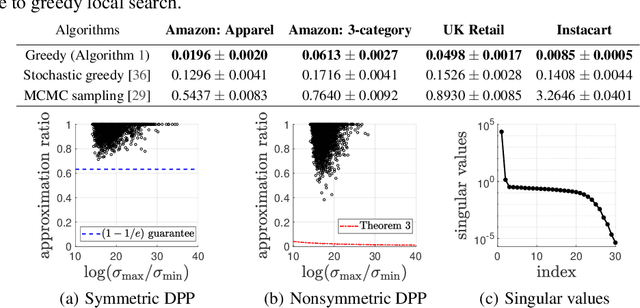
Determinantal point processes (DPPs) have attracted significant attention from the machine learning community for their ability to model subsets drawn from a large collection of items. Recent work shows that nonsymmetric DPP kernels have significant advantages over symmetric kernels in terms of modeling power and predictive performance. However, the nonsymmetric kernel learning algorithm from prior work has computational complexity that is cubic in the size of the DPP ground set, from which subsets are drawn, making it impractical to use at large scales. In this work, we propose a new decomposition for nonsymmetric DPP kernels that induces linear-time complexity for learning and approximate maximum a posteriori (MAP) inference. We also prove a lower bound on the quality of this MAP approximation. Through evaluation on real-world datasets, we show that our new decomposition not only scales better, but also matches or exceeds the predictive performance of prior work.

Embedding models for recommendation under contextual constraints

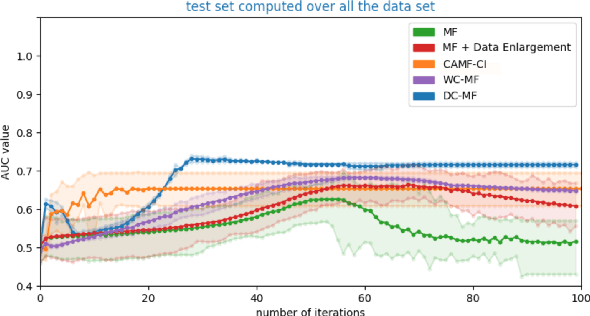
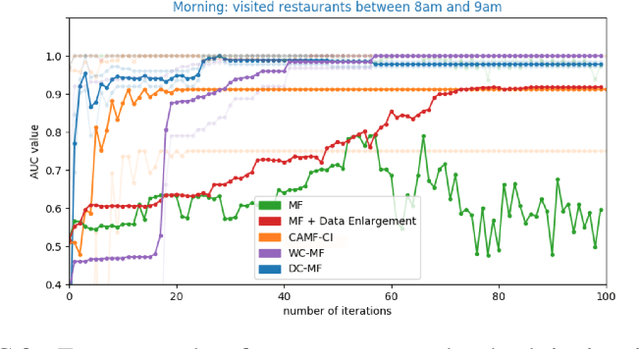
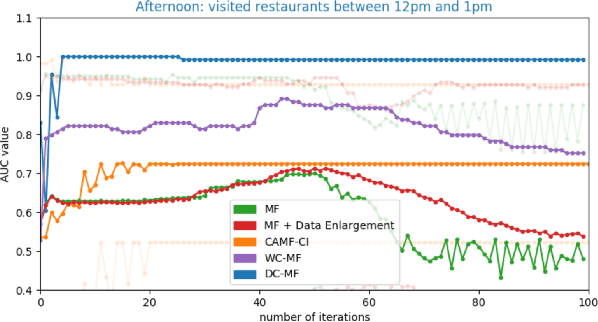
Embedding models, which learn latent representations of users and items based on user-item interaction patterns, are a key component of recommendation systems. In many applications, contextual constraints need to be applied to refine recommendations, e.g. when a user specifies a price range or product category filter. The conventional approach, for both context-aware and standard models, is to retrieve items and apply the constraints as independent operations. The order in which these two steps are executed can induce significant problems. For example, applying constraints a posteriori can result in incomplete recommendations or low-quality results for the tail of the distribution (i.e., less popular items). As a result, the additional information that the constraint brings about user intent may not be accurately captured. In this paper we propose integrating the information provided by the contextual constraint into the similarity computation, by merging constraint application and retrieval into one operation in the embedding space. This technique allows us to generate high-quality recommendations for the specified constraint. Our approach learns constraints representations jointly with the user and item embeddings. We incorporate our methods into a matrix factorization model, and perform an experimental evaluation on one internal and two real-world datasets. Our results show significant improvements in predictive performance compared to context-aware and standard models.