Unified PAC-Bayesian Study of Pessimism for Offline Policy Learning with Regularized Importance Sampling

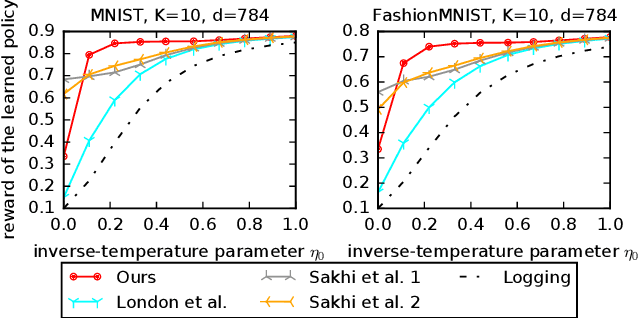
Off-policy learning (OPL) often involves minimizing a risk estimator based on importance weighting to correct bias from the logging policy used to collect data. However, this method can produce an estimator with a high variance. A common solution is to regularize the importance weights and learn the policy by minimizing an estimator with penalties derived from generalization bounds specific to the estimator. This approach, known as pessimism, has gained recent attention but lacks a unified framework for analysis. To address this gap, we introduce a comprehensive PAC-Bayesian framework to examine pessimism with regularized importance weighting. We derive a tractable PAC-Bayesian generalization bound that universally applies to common importance weight regularizations, enabling their comparison within a single framework. Our empirical results challenge common understanding, demonstrating the effectiveness of standard IW regularization techniques.

Bayesian Off-Policy Evaluation and Learning for Large Action Spaces

In interactive systems, actions are often correlated, presenting an opportunity for more sample-efficient off-policy evaluation (OPE) and learning (OPL) in large action spaces. We introduce a unified Bayesian framework to capture these correlations through structured and informative priors. In this framework, we propose sDM, a generic Bayesian approach designed for OPE and OPL, grounded in both algorithmic and theoretical foundations. Notably, sDM leverages action correlations without compromising computational efficiency. Moreover, inspired by online Bayesian bandits, we introduce Bayesian metrics that assess the average performance of algorithms across multiple problem instances, deviating from the conventional worst-case assessments. We analyze sDM in OPE and OPL, highlighting the benefits of leveraging action correlations. Empirical evidence showcases the strong performance of sDM.

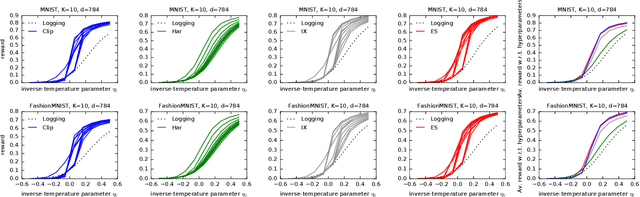
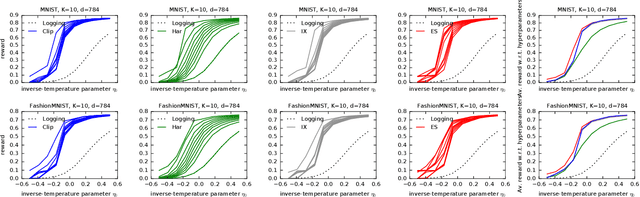
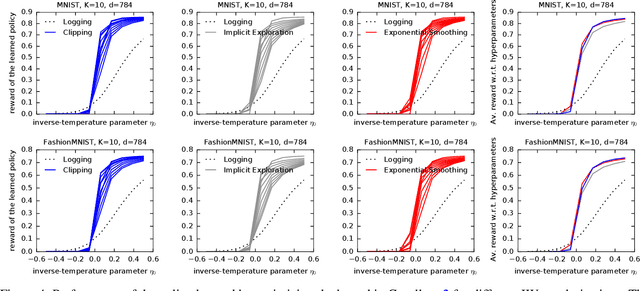
Exponential Smoothing for Off-Policy Learning

Off-policy learning (OPL) aims at finding improved policies from logged bandit data, often by minimizing the inverse propensity scoring (IPS) estimator of the risk. In this work, we investigate a smooth regularization for IPS, for which we derive a two-sided PAC-Bayes generalization bound. The bound is tractable, scalable, interpretable and provides learning certificates. In particular, it is also valid for standard IPS without making the assumption that the importance weights are bounded. We demonstrate the relevance of our approach and its favorable performance through a set of learning tasks. Since our bound holds for standard IPS, we are able to provide insight into when regularizing IPS is useful. Namely, we identify cases where regularization might not be needed. This goes against the belief that, in practice, clipped IPS often enjoys favorable performance than standard IPS in OPL.

Statistical guarantees for generative models without domination

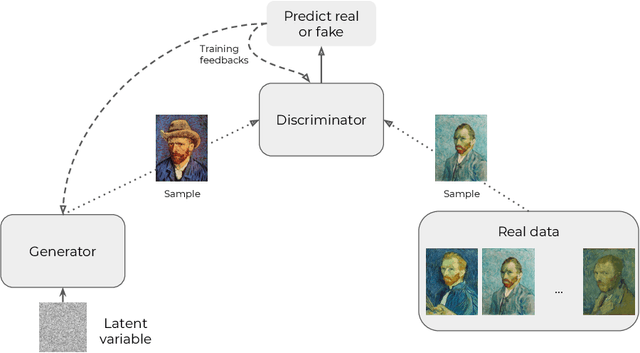
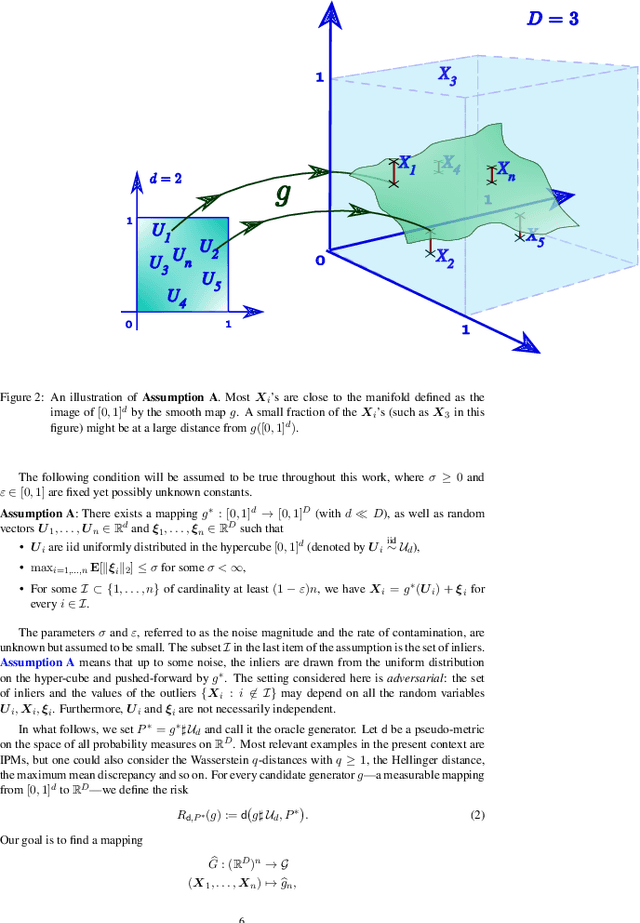
In this paper, we introduce a convenient framework for studying (adversarial) generative models from a statistical perspective. It consists in modeling the generative device as a smooth transformation of the unit hypercube of a dimension that is much smaller than that of the ambient space and measuring the quality of the generative model by means of an integral probability metric. In the particular case of integral probability metric defined through a smoothness class, we establish a risk bound quantifying the role of various parameters. In particular, it clearly shows the impact of dimension reduction on the error of the generative model.

Scalable Learning and MAP Inference for Nonsymmetric Determinantal Point Processes

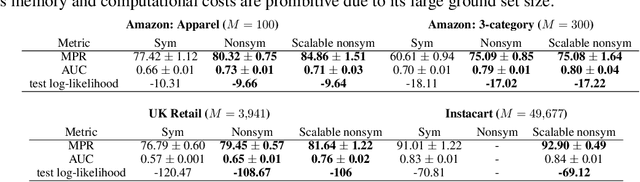
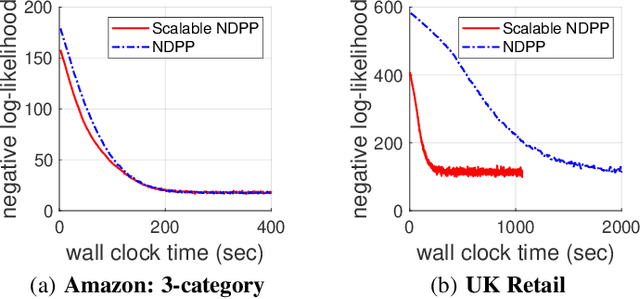
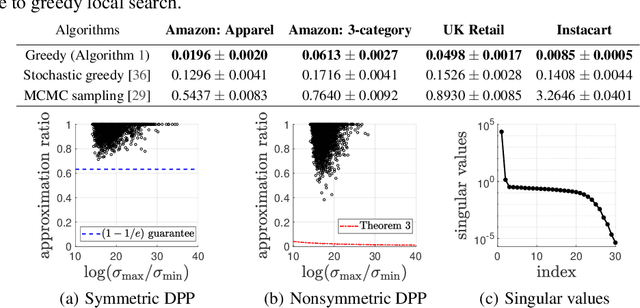
Determinantal point processes (DPPs) have attracted significant attention from the machine learning community for their ability to model subsets drawn from a large collection of items. Recent work shows that nonsymmetric DPP kernels have significant advantages over symmetric kernels in terms of modeling power and predictive performance. However, the nonsymmetric kernel learning algorithm from prior work has computational complexity that is cubic in the size of the DPP ground set, from which subsets are drawn, making it impractical to use at large scales. In this work, we propose a new decomposition for nonsymmetric DPP kernels that induces linear-time complexity for learning and approximate maximum a posteriori (MAP) inference. We also prove a lower bound on the quality of this MAP approximation. Through evaluation on real-world datasets, we show that our new decomposition not only scales better, but also matches or exceeds the predictive performance of prior work.

Propose, Test, Release: Differentially private estimation with high probability

We derive concentration inequalities for differentially private median and mean estimators building on the "Propose, Test, Release" (PTR) mechanism introduced by Dwork and Lei (2009). We introduce a new general version of the PTR mechanism that allows us to derive high probability error bounds for differentially private estimators. Our algorithms provide the first statistical guarantees for differentially private estimation of the median and mean without any boundedness assumptions on the data, and without assuming that the target population parameter lies in some known bounded interval. Our procedures do not rely on any truncation of the data and provide the first sub-Gaussian high probability bounds for differentially private median and mean estimation, for possibly heavy tailed random variables.

Differentially private sub-Gaussian location estimators

We tackle the problem of estimating a location parameter with differential privacy guarantees and sub-Gaussian deviations. Recent work in statistics has focused on the study of estimators that achieve sub-Gaussian type deviations even for heavy tailed data. We revisit some of these estimators through the lens of differential privacy and show that a naive application of the Laplace mechanism can lead to sub-optimal results. We design two private algorithms for estimating the median that lead to estimators with sub-Gaussian type errors. Unlike most existing differentially private median estimators, both algorithms are well defined for unbounded random variables that are not even required to have finite moments. We then turn to the problem of sub-Gaussian mean estimation and show that under heavy tails natural differentially private alternatives lead to strictly worse deviations than their non-private sub-Gaussian counterparts. This is in sharp contrast with recent results that show that from an asymptotic perspective the cost of differential privacy is negligible.

Learning Nonsymmetric Determinantal Point Processes

Determinantal point processes (DPPs) have attracted substantial attention as an elegant probabilistic model that captures the balance between quality and diversity within sets. DPPs are conventionally parameterized by a positive semi-definite kernel matrix, and this symmetric kernel encodes only repulsive interactions between items. These so-called symmetric DPPs have significant expressive power, and have been successfully applied to a variety of machine learning tasks, including recommendation systems, information retrieval, and automatic summarization, among many others. Efficient algorithms for learning symmetric DPPs and sampling from these models have been reasonably well studied. However, relatively little attention has been given to nonsymmetric DPPs, which relax the symmetric constraint on the kernel. Nonsymmetric DPPs allow for both repulsive and attractive item interactions, which can significantly improve modeling power, resulting in a model that may better fit for some applications. We present a method that enables a tractable algorithm, based on maximum likelihood estimation, for learning nonsymmetric DPPs from data composed of observed subsets. Our method imposes a particular decomposition of the nonsymmetric kernel that enables such tractable learning algorithms, which we analyze both theoretically and experimentally. We evaluate our model on synthetic and real-world datasets, demonstrating improved predictive performance compared to symmetric DPPs, which have previously shown strong performance on modeling tasks associated with these datasets.

A nonasymptotic law of iterated logarithm for robust online estimators

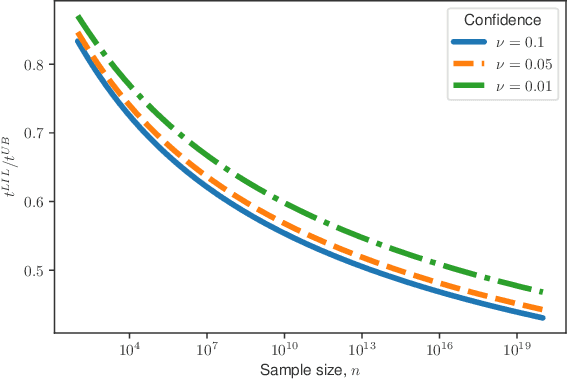
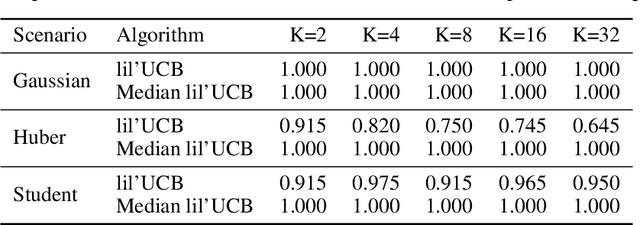
In this paper, we provide tight deviation bounds for M-estimators, which are valid with a prescribed probability for every sample size. M-estimators are ubiquitous in machine learning and statistical learning theory. They are used both for defining prediction strategies and for evaluating their precision. Our deviation bounds can be seen as a non-asymptotic version of the law of iterated logarithm. They are established under general assumptions such as Lipschitz continuity of the loss function and (local) curvature of the population risk. These conditions are satisfied for most examples used in machine learning, including those that are known to be robust to outliers and to heavy tailed distributions. To further highlight the scope of applicability of the obtained results, a new algorithm, with provably optimal theoretical guarantees, for the best arm identification in a stochastic multi-arm bandit setting is presented. Numerical experiments illustrating the validity of the algorithm are reported.

Best Arm Identification for Contaminated Bandits

This paper studies active learning in the context of robust statistics. Specifically, we propose a variant of the Best Arm Identification problem for \emph{contaminated bandits}, where each arm pull has probability $\varepsilon$ of generating a sample from an arbitrary contamination distribution instead of the true underlying distribution. The goal is to identify the best (or approximately best) true distribution with high probability, with a secondary goal of providing guarantees on the quality of this distribution. The primary challenge of the contaminated bandit setting is that the true distributions are only partially identifiable, even with infinite samples. To address this, we first develop tight, non-asymptotic sample complexity bounds for high-probability estimation of the first two robust moments (median and median absolute deviation) from contaminated samples, which may be of independent interest. Using these results, we adapt several classical Best Arm Identification algorithms to the contaminated bandit setting and derive sample complexity upper bounds for our problem. Finally, we provide matching information-theoretic lower bounds on the sample complexity (up to a small logarithmic factor). Our results suggest an inherent robustness of classical Best Arm Identification algorithms.