Scalable Learning and MAP Inference for Nonsymmetric Determinantal Point Processes

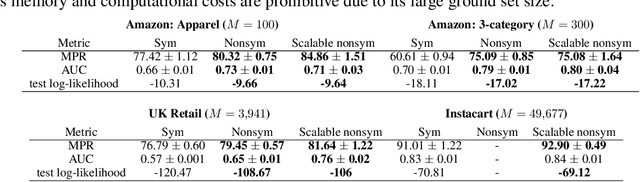
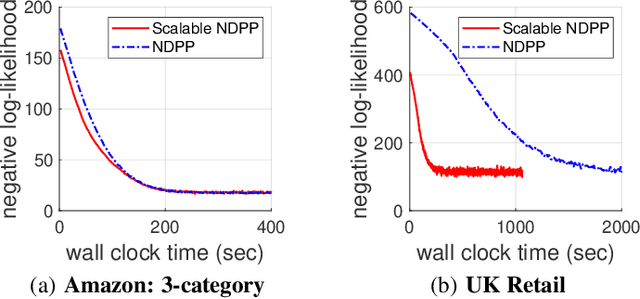
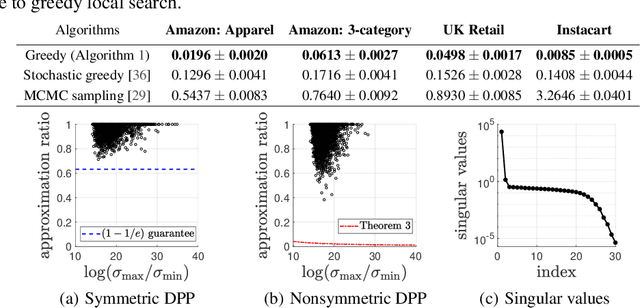
Determinantal point processes (DPPs) have attracted significant attention from the machine learning community for their ability to model subsets drawn from a large collection of items. Recent work shows that nonsymmetric DPP kernels have significant advantages over symmetric kernels in terms of modeling power and predictive performance. However, the nonsymmetric kernel learning algorithm from prior work has computational complexity that is cubic in the size of the DPP ground set, from which subsets are drawn, making it impractical to use at large scales. In this work, we propose a new decomposition for nonsymmetric DPP kernels that induces linear-time complexity for learning and approximate maximum a posteriori (MAP) inference. We also prove a lower bound on the quality of this MAP approximation. Through evaluation on real-world datasets, we show that our new decomposition not only scales better, but also matches or exceeds the predictive performance of prior work.