A Principle of Least Action for the Training of Neural Networks
Paper and Code
Sep 17, 2020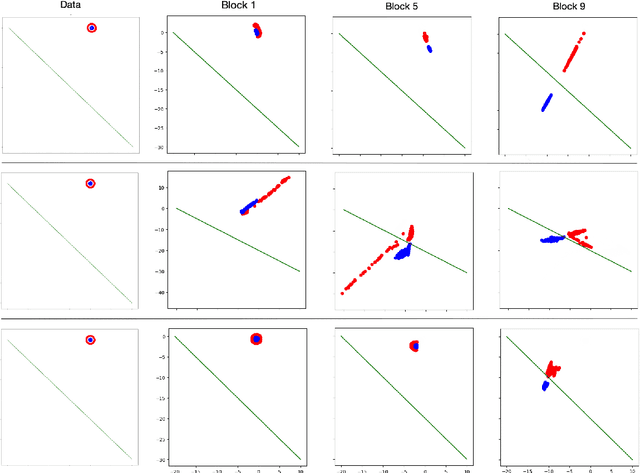
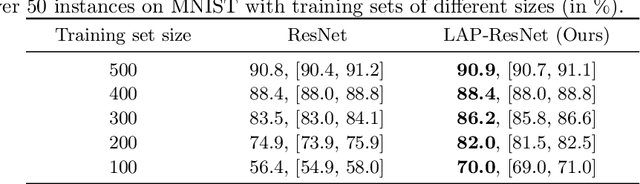
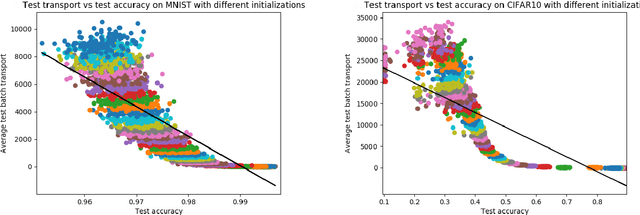
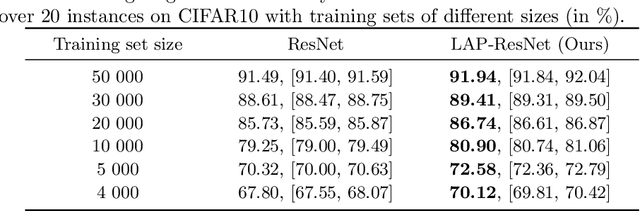
Neural networks have been achieving high generalization performance on many tasks despite being highly over-parameterized. Since classical statistical learning theory struggles to explain this behavior, much effort has recently been focused on uncovering the mechanisms behind it, in the hope of developing a more adequate theoretical framework and having a better control over the trained models. In this work, we adopt an alternate perspective, viewing the neural network as a dynamical system displacing input particles over time. We conduct a series of experiments and, by analyzing the network's behavior through its displacements, we show the presence of a low kinetic energy displacement bias in the transport map of the network, and link this bias with generalization performance. From this observation, we reformulate the learning problem as follows: finding neural networks which solve the task while transporting the data as efficiently as possible. This offers a novel formulation of the learning problem which allows us to provide regularity results for the solution network, based on Optimal Transport theory. From a practical viewpoint, this allows us to propose a new learning algorithm, which automatically adapts to the complexity of the given task, and leads to networks with a high generalization ability even in low data regimes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge