NeurIPS 2024 ML4CFD Competition: Results and Retrospective Analysis

The integration of machine learning (ML) into the physical sciences is reshaping computational paradigms, offering the potential to accelerate demanding simulations such as computational fluid dynamics (CFD). Yet, persistent challenges in accuracy, generalization, and physical consistency hinder the practical deployment of ML models in scientific domains. To address these limitations and systematically benchmark progress, we organized the ML4CFD competition, centered on surrogate modeling for aerodynamic simulations over two-dimensional airfoils. The competition attracted over 240 teams, who were provided with a curated dataset generated via OpenFOAM and evaluated through a multi-criteria framework encompassing predictive accuracy, physical fidelity, computational efficiency, and out-of-distribution generalization. This retrospective analysis reviews the competition outcomes, highlighting several approaches that outperformed baselines under our global evaluation score. Notably, the top entry exceeded the performance of the original OpenFOAM solver on aggregate metrics, illustrating the promise of ML-based surrogates to outperform traditional solvers under tailored criteria. Drawing from these results, we analyze the key design principles of top submissions, assess the robustness of our evaluation framework, and offer guidance for future scientific ML challenges.

NeurIPS 2025 E2LM Competition : Early Training Evaluation of Language Models

Existing benchmarks have proven effective for assessing the performance of fully trained large language models. However, we find striking differences in the early training stages of small models, where benchmarks often fail to provide meaningful or discriminative signals. To explore how these differences arise, this competition tackles the challenge of designing scientific knowledge evaluation tasks specifically tailored for measuring early training progress of language models. Participants are invited to develop novel evaluation methodologies or adapt existing benchmarks to better capture performance differences among language models. To support this effort, we provide three pre-trained small models (0.5B, 1B, and 3B parameters), along with intermediate checkpoints sampled during training up to 200B tokens. All experiments and development work can be run on widely available free cloud-based GPU platforms, making participation accessible to researchers with limited computational resources. Submissions will be evaluated based on three criteria: the quality of the performance signal they produce, the consistency of model rankings at 1 trillion tokens of training, and their relevance to the scientific knowledge domain. By promoting the design of tailored evaluation strategies for early training, this competition aims to attract a broad range of participants from various disciplines, including those who may not be machine learning experts or have access to dedicated GPU resources. Ultimately, this initiative seeks to make foundational LLM research more systematic and benchmark-informed from the earliest phases of model development.

A new methodology to decompose a parametric domain using reduced order data manifold in machine learning

We propose a new methodology for parametric domain decomposition using iterative principal component analysis. Starting with iterative principle component analysis, the high dimension manifold is reduced to the lower dimension manifold. Moreover, two approaches are developed to reconstruct the inverse projector to project from the lower data component to the original one. Afterward, we provide a detailed strategy to decompose the parametric domain based on the low dimension manifold. Finally, numerical examples of harmonic transport problem are given to illustrate the efficiency and effectiveness of the proposed method comparing to the classical meta-models such as neural networks.

An adaptive sampling algorithm for data-generation to build a data-manifold for physical problem surrogate modeling

Physical models classically involved Partial Differential equations (PDE) and depending of their underlying complexity and the level of accuracy required, and known to be computationally expensive to numerically solve them. Thus, an idea would be to create a surrogate model relying on data generated by such solver. However, training such a model on an imbalanced data have been shown to be a very difficult task. Indeed, if the distribution of input leads to a poor response manifold representation, the model may not learn well and consequently, it may not predict the outcome with acceptable accuracy. In this work, we present an Adaptive Sampling Algorithm for Data Generation (ASADG) involving a physical model. As the initial input data may not accurately represent the response manifold in higher dimension, this algorithm iteratively adds input data into it. At each step the barycenter of each simplicial complex, that the manifold is discretized into, is added as new input data, if a certain threshold is satisfied. We demonstrate the efficiency of the data sampling algorithm in comparison with LHS method for generating more representative input data. To do so, we focus on the construction of a harmonic transport problem metamodel by generating data through a classical solver. By using such algorithm, it is possible to generate the same number of input data as LHS while providing a better representation of the response manifold.

Constrained Recurrent Bayesian Forecasting for Crack Propagation

Predictive maintenance of railway infrastructure, especially railroads, is essential to ensure safety. However, accurate prediction of crack evolution represents a major challenge due to the complex interactions between intrinsic and external factors, as well as measurement uncertainties. Effective modeling requires a multidimensional approach and a comprehensive understanding of these dynamics and uncertainties. Motivated by an industrial use case based on collected real data containing measured crack lengths, this paper introduces a robust Bayesian multi-horizon approach for predicting the temporal evolution of crack lengths on rails. This model captures the intricate interplay between various factors influencing crack growth. Additionally, the Bayesian approach quantifies both epistemic and aleatoric uncertainties, providing a confidence interval around predictions. To enhance the model's reliability for railroad maintenance, specific constraints are incorporated. These constraints limit non-physical crack propagation behavior and prioritize safety. The findings reveal a trade-off between prediction accuracy and constraint compliance, highlighting the nuanced decision-making process in model training. This study offers insights into advanced predictive modeling for dynamic temporal forecasting, particularly in railway maintenance, with potential applications in other domains.

NeurIPS 2024 ML4CFD Competition: Harnessing Machine Learning for Computational Fluid Dynamics in Airfoil Design

The integration of machine learning (ML) techniques for addressing intricate physics problems is increasingly recognized as a promising avenue for expediting simulations. However, assessing ML-derived physical models poses a significant challenge for their adoption within industrial contexts. This competition is designed to promote the development of innovative ML approaches for tackling physical challenges, leveraging our recently introduced unified evaluation framework known as Learning Industrial Physical Simulations (LIPS). Building upon the preliminary edition held from November 2023 to March 2024, this iteration centers on a task fundamental to a well-established physical application: airfoil design simulation, utilizing our proposed AirfRANS dataset. The competition evaluates solutions based on various criteria encompassing ML accuracy, computational efficiency, Out-Of-Distribution performance, and adherence to physical principles. Notably, this competition represents a pioneering effort in exploring ML-driven surrogate methods aimed at optimizing the trade-off between computational efficiency and accuracy in physical simulations. Hosted on the Codabench platform, the competition offers online training and evaluation for all participating solutions.

ML4PhySim : Machine Learning for Physical Simulations Challenge (The airfoil design)

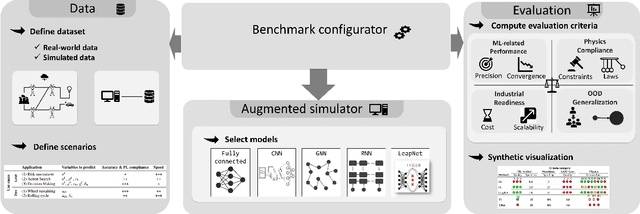
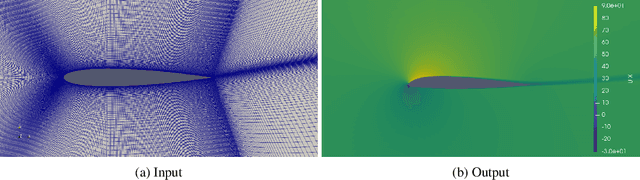
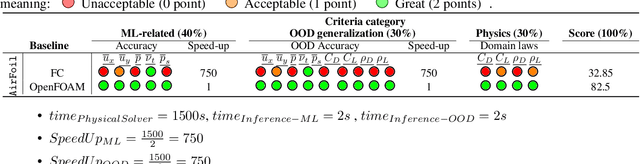
The use of machine learning (ML) techniques to solve complex physical problems has been considered recently as a promising approach. However, the evaluation of such learned physical models remains an important issue for industrial use. The aim of this competition is to encourage the development of new ML techniques to solve physical problems using a unified evaluation framework proposed recently, called Learning Industrial Physical Simulations (LIPS). We propose learning a task representing a well-known physical use case: the airfoil design simulation, using a dataset called AirfRANS. The global score calculated for each submitted solution is based on three main categories of criteria covering different aspects, namely: ML-related, Out-Of-Distribution, and physical compliance criteria. To the best of our knowledge, this is the first competition addressing the use of ML-based surrogate approaches to improve the trade-off computational cost/accuracy of physical simulation.The competition is hosted by the Codabench platform with online training and evaluation of all submitted solutions.

Interpretable learning of effective dynamics for multiscale systems

The modeling and simulation of high-dimensional multiscale systems is a critical challenge across all areas of science and engineering. It is broadly believed that even with today's computer advances resolving all spatiotemporal scales described by the governing equations remains a remote target. This realization has prompted intense efforts to develop model order reduction techniques. In recent years, techniques based on deep recurrent neural networks have produced promising results for the modeling and simulation of complex spatiotemporal systems and offer large flexibility in model development as they can incorporate experimental and computational data. However, neural networks lack interpretability, which limits their utility and generalizability across complex systems. Here we propose a novel framework of Interpretable Learning Effective Dynamics (iLED) that offers comparable accuracy to state-of-the-art recurrent neural network-based approaches while providing the added benefit of interpretability. The iLED framework is motivated by Mori-Zwanzig and Koopman operator theory, which justifies the choice of the specific architecture. We demonstrate the effectiveness of the proposed framework in simulations of three benchmark multiscale systems. Our results show that the iLED framework can generate accurate predictions and obtain interpretable dynamics, making it a promising approach for solving high-dimensional multiscale systems.

Hybrid data driven/thermal simulation model for comfort assessment

Machine learning models improve the speed and quality of physical models. However, they require a large amount of data, which is often difficult and costly to acquire. Predicting thermal comfort, for example, requires a controlled environment, with participants presenting various characteristics (age, gender, ...). This paper proposes a method for hybridizing real data with simulated data for thermal comfort prediction. The simulations are performed using Modelica Language. A benchmarking study is realized to compare different machine learning methods. Obtained results look promising with an F1 score of 0.999 obtained using the random forest model.

Rail Crack Propagation Forecasting Using Multi-horizons RNNs

The prediction of rail crack length propagation plays a crucial role in the maintenance and safety assessment of materials and structures. Traditional methods rely on physical models and empirical equations such as Paris law, which often have limitations in capturing the complex nature of crack growth. In recent years, machine learning techniques, particularly Recurrent Neural Networks (RNNs), have emerged as promising methods for time series forecasting. They allow to model time series data, and to incorporate exogenous variables into the model. The proposed approach involves collecting real data on the French rail network that includes historical crack length measurements, along with relevant exogenous factors that may influence crack growth. First, a pre-processing phase was performed to prepare a consistent data set for learning. Then, a suitable Bayesian multi-horizons recurrent architecture was designed to model the crack propagation phenomenon. Obtained results show that the Multi-horizons model outperforms state-of-the-art models such as LSTM and GRU.