Multi-scale Physical Representations for Approximating PDE Solutions with Graph Neural Operators
Paper and Code
Jun 29, 2022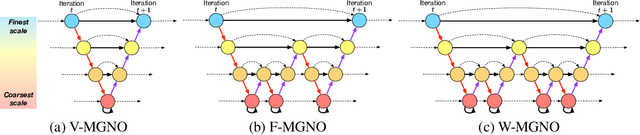
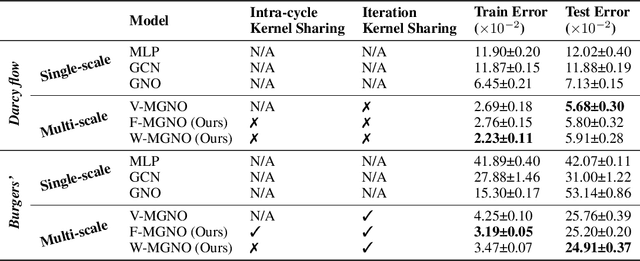
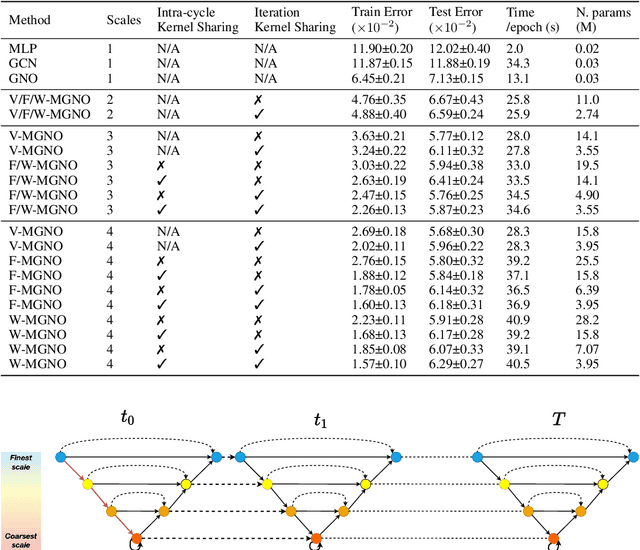
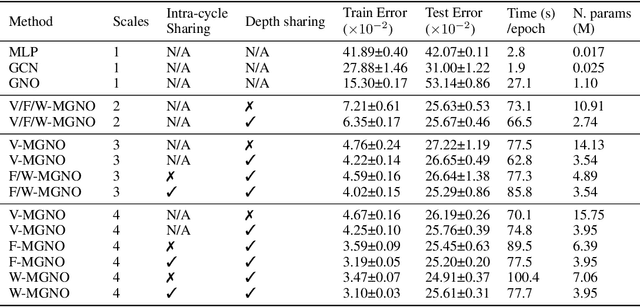
Representing physical signals at different scales is among the most challenging problems in engineering. Several multi-scale modeling tools have been developed to describe physical systems governed by \emph{Partial Differential Equations} (PDEs). These tools are at the crossroad of principled physical models and numerical schema. Recently, data-driven models have been introduced to speed-up the approximation of PDE solutions compared to numerical solvers. Among these recent data-driven methods, neural integral operators are a class that learn a mapping between function spaces. These functions are discretized on graphs (meshes) which are appropriate for modeling interactions in physical phenomena. In this work, we study three multi-resolution schema with integral kernel operators that can be approximated with \emph{Message Passing Graph Neural Networks} (MPGNNs). To validate our study, we make extensive MPGNNs experiments with well-chosen metrics considering steady and unsteady PDEs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge